基于动力有限元方法的典型砌体结构爆破振动安全标准的探讨

魏海霞，陈士海，张安康

(1.河南理工大学 土木工程学院，河南 焦作 454003;2.山东科技大学 土木建筑学院，青岛 266510)

基于动力有限元方法的典型砌体结构爆破振动安全标准的探讨

魏海霞1，2，陈士海2，张安康2

(1.河南理工大学 土木工程学院，河南 焦作 454003;2.山东科技大学 土木建筑学院，青岛 266510)

采用动力有限元方法，参照爆区现场的一实际三层砌体房屋结构，建立三维空间实体模型，并将底层的爆破地震波监测信号加载到砌体结构模型的基底，求解出有限元模拟的砌体结构其它各层的爆破振动响应值，并与监测结果进行了比较分析。对常见的2层～4层砌体结构房屋，各取一种典型结构在底部节点垂直方向上施加不同主频的爆破地震波进行动力有限元建模并模拟开裂过程，通过定义结构单元的临界失效状态来寻求典型砌体结构房屋的爆破振动安全标准值，并给出了2～4层典型砌体结构房屋在各主频段爆破地震波作用下的爆破振动安全标准。结果表明，现行的《爆破安全规程》中基于工程经验及宏观调查资料基础上制定出的爆破振动安全标准过于粗糙和笼统，对于同类建筑，没有考虑到结构个体的振动特性差异，并不能保证所有结构物的安全，不具有普适性。

砌体结构;动力有限元方法;临界失效状态;安全标准

砌体结构力学性能较为复杂，给砌体结构房屋振动效应及抗震性能的研究带来诸多困难。目前专家学者采用较多的研究方法有:振动台试验、时程分析法和动力有限元法。振动台试验是研究建筑结构抗震性能和抗震能力的有效手段，但由于利用振动台开展的结构抗震试验［1－2］需耗费大量人力物力，并且采用的缩尺试验模型和原型房屋的质量和刚度比不同，试验模型和原型房屋的动力特性存在不完全相似，势必造成研究结果和实际有所出入。时程分析方法是目前研究结构在强震作用下弹塑性反应以及特别重要结构抗震设计时采用的最主要方法。时程分析法的结果虽然较为精确，但其计算量大、对计算机的要求较高，基于简化的层间模型［3］或杆系模型［4］的时程分析方法一般很难直接给出与结构变形对应的材料应力—应变状态以及结构破坏形态等特征，需要借助进一步的分析得到，动力有限元法在时程分析中的应用恰好弥补了这一不足。

动力有限元分析方法是一种有力的分析工具，可以对结构从开始受荷、开裂直至破坏的全过程进行非线性动力分析并可获得结构整个时程的受力性能信息。但是由于砌体结构非线性地震响应动力有限元分析难度高，计算代价大，目前动力有限元模型主要用于分析结构部件或局部结构的动力非线性问题［5］以及参数研究和模型试验［6］的计算模拟，很少进行砌体房屋三维空间结构的非线性动力有限元分析。

本文采用动力有限元方法，对常见的2～4层砌体结构房屋，建立三维空间实体有限元模型，然后在结构底部节点施加爆破地震波并进行相关的动力分析，通过定义结构的失效临界状态来寻求典型砌体结构房屋的爆破振动安全标准。

1 砌体结构本构模型选取

砌体是由砌块和砂浆组成的二相复合材料，目前砌体结构的有限元分析模型可以分为以 Lotf、Shing等［7］学者为代表将砌块、砂浆及灰缝节点分别以不同单元进行模拟的离散化模型和以Heymann、Pande、Lourenco和 Antonella 等［1，6］学者为代表的连续化模型。前者将砌块和砂浆分别考虑成不同单元，建模繁琐，耗费巨大机时，且弹性模量离散型太大，其黏结强度不易模拟，仅适用于模拟小型试验砌体的破坏行为。因此本文采取第二种模型对结构中砌体材料墙体使用同一种连续化材料类型进行整体建模。

本文研究的砌体结构房屋均为典型的低层(2层～4层)砖混结构，墙体为砖或石砌体材料，梁、楼板及构造柱为钢筋混凝土材料。砌体的材料本构采用LS层DYNA中的Plastic Kinematic模型，该模型定义了结构单元的失效应变值。另外，由于砌体的抗拉强度较低，可通过*Mat_Add_Erosion定义失效(拉)应力值的双重标准来判定单元是否失效，先达到任一临界状态就认定单元出现失效，失效时刻在模型分析中认为砌体结构开始出现裂缝，然后继续计算时失效单元被删除。本文中各材料参数取值见表1。其中有限元模型单元采取映射网格划分中的等线段划分方式，单元大小控制在80 mm～100 mm。

表1 材料模型参数列表Tab.1 Parameters of material model

2 砌体结构爆破振动响应的现场监测及有限元模拟

2.1 工程概况与测点布置

泉厦高速公路扩建工程大坪山新建隧道场区属于构造剥蚀微丘地貌，山顶地形波状起伏，平均高程在80 m～100 m，表层多为残坡积土，下覆燕山早期侵入花岗岩及其风化层，其构造条件相对稳定，未见断裂带通过，岩体以整体结构为主，局部为块状砌体结构，洞身有节理裂隙发育带。大坪山隧道山顶正上方及其附近分布有大量的2层～4层砌体结构居民住房，其中居民住房离爆源最小距离只有47 m左右。为研究大坪山隧道爆破开挖引起的附近砌体结构房屋的爆破振动响应，使用成都中科动态有限公司生产的IDTS3850爆破震动记录仪及配套三方向的速度传感器对爆区低层砌体房屋进行了布点监测，在此选用一典型三层砌体房屋的监测结果进行分析。其中砌体房屋三层层高均为3.5 m，墙厚240 mm，梁高250 m，板厚150 m。

在爆破振动作用下，房屋墙角是最能反应房屋能否发生破坏的主要部位，这是由于爆破地震波频繁而连续的压、扭作用总在墙角间发生，结构由于变形反应和裂缝而产生的应力在墙角处得到了集中反应［8］。故在三层砌体房屋靠近爆源方向的1层～3层楼面及屋顶的对应墙角处，各布置一测点，分别为测点1～4。

2.2 砌体结构爆破振动响应的现场监测结果

在三层砌体结构房屋测点1～4处现场监测到的爆破振动峰值速度数据见表2。

表2 现场监测的测点1～4处爆破振动峰值速度Tab.2 Peak velocity values of blasting vibration at measuring points of 1 ～4 by field observation

2.3 砌体结构爆破振动响应的有限元模拟

依照上述的本构模型及结构实际尺寸，建立三层砌体结构房屋的有限元模型(见图1)，将测点1垂直方向、水平径向、水平切向的速度响应数据作为外部激励荷载施加到有限元模型的基础底面节点组对应的三个方向，在与测点对应的有限元模型二三层及屋顶的墙角位置处设置加密节点，修改好K文件后使用LS－DYNA求解器进行计算，然后通过LS－PREPOST查看各测点的爆破振动响应结果，其中有限元模拟的三层砌体房屋各测点的爆破振动峰值速度见表3，有限元模拟的测点2处的速度响应时程曲线见图2。

图1 三层砌体房屋的有限元模型Fig.1 Finite element model of the three-storey building

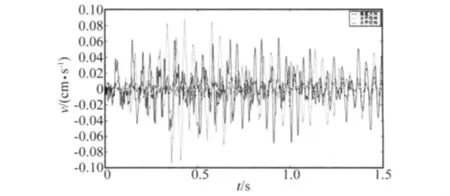
图2 有限元模拟的测点2处的速度响应时程曲线Fig.2 Time history of velocity response at point 2 by finite element simulation

表3 有限元模拟的测点2～4处爆破振动峰值速度Tab.3 Peak velocity values of blasting vibration at measuring points of 2 ～4 by finite element simulation

2.4 结果比较分析

通过比较表2与表3中测点2～测点4中各方向的爆破振动峰值速度值可知:大部分结果比较接近，其中有一部分结果差值较大，但是其值都保持在同一个数量级内。引起有限元模拟值与实测值产生误差的原因，有以下几方面:

(1)测点1处的监测值是在底层室内水平面上所测，而对有限元模型进行爆破地震波加载时，是直接加载到砌体结构模型基础圈梁的底部节点上，加载的方式采取一致激励而没有考虑地震波衰减的因素。

(2)砌体结构有限元模型做了很多简化，比如:①实际房屋的一层外部墙体有部分料石砌筑，在建模时统一定义成了砖材料;② 有限元模型中没有分别模拟砌体材料的砌块和砂浆，钢筋混凝土材料的钢筋和混凝土，而是分别作为一种连续性复合材料来处理;③为缩减计算单元，有限元模型统统没有考虑砌体房屋的小尺寸构件及附属设施，如门垛、门窗过梁、楼梯、墙面及楼面抹灰等。

(3)有限元模型没有考虑被监测房屋所处的地形地质以及砌体房屋的维护状况。

(4)虽然监测了数个炮次，但是使仪器同时触发而得到的有效数据太少，没有得到具有统计特征的监测数据来验证有限元模拟结果。

相对为理想环境下开展的实验室试验，本文所监测的数据在更为复杂的工程环境下进行，故有限元模拟的结构爆破振动响应结果与实测值之间的误差，在可接受范围。

3 典型砌体结构的爆破振动安全标准研究

3.1 概述

在我国的爆破工程中，人们对结构在爆破地震作用下的安全评估多是依据我国《爆破安全规程》(GB6722—2003)中的爆破振动安全允许标准来进行。要说明的是，一个爆破工程产生的爆破地震符合爆破振动安全允许标准只是一个最基本的要求，但并不能完全确保建筑物的安全。其缘由在于爆破振动安全允许标准虽然对建筑物保护对象类别进行了划分以及对爆破地震做出了要求，却没有考虑结构类型、材料参数等建筑物本身的振动特性。通过动力有限元法求解出的具体建筑结构的爆破振动安全标准恰恰综合考虑了上述诸多因素，研究的更加具体和有针对性。限于精力和篇幅，本文仅对常见的2～4层砌体结构房屋，各取一种典型结构在底部节点施加爆破地震波进行动力有限元建模并模拟开裂过程，通过定义失效临界状态来寻求典型砌体结构房屋的爆破振动安全标准值。

3.2 砌体结构的爆破振动安全标准的确定方法与步骤

3.2.1 砌体结构的爆破振动安全标准的确定方法

寻求砌体结构的爆破振动安全标准，简单地说来，就是确定砌体结构某构件刚要出现开裂的临界状态下的输入爆破地震波的幅值。在进行动力有限元分析时虽然定义了失效应变和失效应力值的破坏标准，在对爆破地震波作用下砌体结构进行实际的动力有限元分析的过程中发现，针对本文所给的结构类型及材料模型，一般是结构单元的第一主应力先达到失效应力值而失效，则砌体结构的临界失效(开裂)状态即结构某单元的第一主应力将要达到失效应力值的瞬时状态。

在实际的有限元分析中，临界失效状态一般不好把握。要么就是施加的激励波的幅值偏小，没有结构单元发生失效，要么就是施加的激励波的幅值偏大，已经有不少单元发生失效。寻求这个临界状态要进行很多次非常耗费机时的循环计算，且寻找的临界状态并不一定是真正意义上的临界失效状态。在此，采取如下处理方法来确定爆破振动安全标准:若输入爆破地震波的幅值等于v1时结构中无单元失效，当幅值增加到1.05v1(增加幅度为5%)时结构中有单元失效，则定义前者状态为结构单元的临界失效状态，并确定v1为爆破振动安全标准值。

3.2.2 砌体结构的爆破振动安全标准的确定步骤

以下将使用上述确定方法来寻求2层～4层典型砌体房屋结构的爆破振动安全标准。具体的操作步骤是:

(1)对2层～4层的砌体房屋，各找一典型结构和合适的材料本构(为方便起见，以下本构模型均参考表1)进行有限元建模。

(2)寻求各主频段的爆破地震速度波作为输入荷载加载到砌体结构的有限元模型基底节点。因为爆破地震波的频带较宽，不可能取遍各个主频的地震波。在本文中，参照《爆破安全规程》中爆破振动安全允许标准的频段划分依据，即取主频在＜10 Hz、10 Hz～50 Hz、50 Hz～100 Hz频段内的实测爆破地震波各一个，持续时间取0.2 s，幅值可通过系数来调节。本文中所取的实测爆破地震波的各参数如下:爆破地震波w1，主频 4.9 Hz，幅值 1.04 cm/s;爆破地震波 w2，主频 36.6 Hz，幅值 0.47 cm/s;爆破地震波 w3，主频 67.7 Hz，幅值0.9 cm/s。另外，从目前的研究成果看来，对同一测点处垂直方向、水平径向与水平切向上各爆破地震波主频与幅值之间的对应关系方面还没有统一明确的定论，故很难选择同时能加载到结构上的三维爆破地震波信号。根据文献［9］中“三维爆破振动中爆破振动安全标准值阀值的选取应以其作用于垂直方向引起的爆破地震响应为准”，因此本文中将所选取的各主频段的爆破地震速度波施加到砌体结构基底节点的垂直方向。

(3)通过查看动力有限元分析结果与调节爆破地震波幅值的交替进行，确定爆破振动安全标准值。

3.3 典型砌体结构的爆破振动安全标准的确定

本文的主要研究对象是2层～4层典型砌体结构房屋，其中二层砌体结构的有限元模型见图3，三层砌体结构选用上述提及的结构类型，有限元模型见图1，四层砌体结构的有限元模型见图4。

首先确定二层砌体房屋在主频＜10 Hz的爆破地震波作用下的爆破振动安全判据。将爆破地震波w1施加到二层砌体房屋底部节点，通过不断改变爆破地震波w1的幅值然后查看后处理结果来寻求临界值。在反复计算分析中发现:当爆破地震波w1的幅值为1.768 cm/s时，无结构单元发生失效，当幅值变为1.856 cm/s(1.768 的 1.05 倍)时，有结构单元发生失效。则可以确定二层砌体房屋在主频＜10 Hz的爆破地震波作用下的爆破振动安全标准值为1.768 cm/s。取砌体结构中在后者状态下失效的某一结构单元(单元编号为96 946)，该单元在两种状态下的第一主应力时程曲线见图5。观察图5中(a)和(b)，可以看出:图(a)中，96 946#单元在失效前的最大的第一主应力为2.51×105Pa，小于表1材料模型参数中所取的失效应力值3×105Pa，故单元未失效;而图(b)中，96 946#单元在0.052 s时刻，第一主应力达到失效应力值3×105Pa，单元在该时刻发生失效后应力值突变为零。

按上述同样的方法，分别求出所给2层～4层砌体结构房屋在各主频段爆破地震波作用下的爆破振动安全标准值，见表4。同时发现，砌体结构在爆破地震波荷载作用下首先发生失效的部位主要集中在结构底层的转角处以及门窗洞口附近的墙体单元，这与天然地震波作用下的砌体结构破坏部位基本一致。

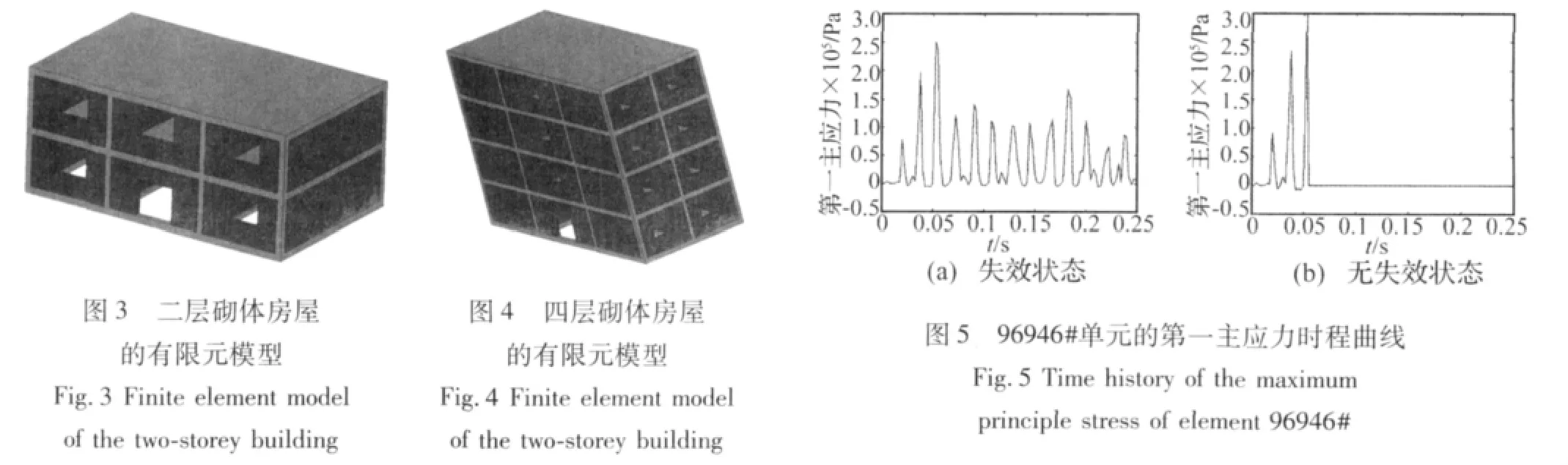
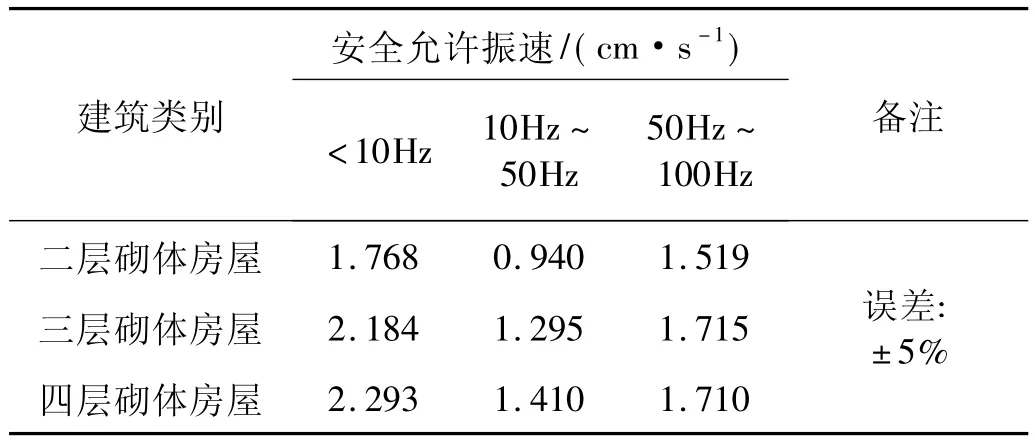
表4 砌体结构房屋的爆破振动安全标准Tab.4 Safety standards of blasting vibration for masonry buildings

3.4 结果分析

将表4与《爆破安全规程》中对“一般砖房、非抗震的大型砌块建筑物”规定的爆破振动安全允许振速值进行对比，后者比前者要大。另外，本文是使用动力有限元法确定建筑结构的爆破振动安全标准的一个初步探索，在分析过程中仍存在如下与实际情况有些出入的地方:

(1)各层砌体结构的有限元模型的结构设计偏保守，梁板均为钢筋混凝土现浇，设有基础圈梁且每层均设置上部圈梁，每道墙与墙的相交处均设置构造柱，按该结构建立的砌体结构将有较强的抗震性能。

(2)有限元模型没考虑砌体房屋的建筑质量、新旧程度、裂隙状况等对本构模型参数取值的影响。

(3)有限元模型的输入荷载以垂直方向爆破地震波代替三维爆破地震波，持续时间没有选取段数较多持时更长的多段微差爆破。

若要综合考虑上述因素的话，表4中的安全允许振速应考虑再除以一个大于1的安全系数，实际得到的安全阀值将更低于《爆破安全规程》。可见，现行的《爆破安全规程》中基于工程经验及宏观调查资料基础上制定出的爆破振动安全标准过于粗糙和笼统，对于同类建筑，没有考虑到结构个体的振动特性差异，并不能保证所有结构物的安全，不具有普适性。

4 结论

本文采用动力有限元方法，参照爆区现场的一实际三层砌体房屋结构，建立三维空间实体模型，并将底层的爆破地震波监测信号加载到砌体结构模型的基底，求解出有限元模拟的砌体结构其它各层的爆破振动响应值，并与监测结果进行了比较分析。对常见的2层～4层砌体结构房屋，各取一种典型结构在底部节点垂直方向上施加不同主频的爆破地震波进行动力有限元建模并模拟开裂过程，通过定义结构单元的失效临界状态来寻求典型砌体结构房屋的爆破振动安全标准值，并给出了2层～4层典型砌体结构房屋在各主频段爆破地震波作用下的爆破振动安全标准。

［1］Buonopane S G，White R N.Pseudodynamic testing of masonry infilled reinforced concrete frame［J］.Journal of Structural Engineering，1999，125(6):578－589.

［2］ Paquette J，Bruneau M.Pseudo-dynamic testing of unreinforced masonry building with flexible diaphragm［J］.Journal of Structural Engineering，2003，129(6):708 －716.

［3］申永康，邵建华，陈建锋.建筑结构爆破地震反应弹塑性精细时程分析［J］.爆炸与冲击，2008，28(1):92－96.

［4］Kim S C，White D W.Nonlinear analysis of a one-story lowrise masonry building with a flexible diaphragm subjected to seismic excitation［J］.Engineering Structures，2004，26:2053－2067.

［5］Milani G，Lourenco P B，Tralli A .Homogenised limit analysis of masonry walls，partⅡ:structural examples［J］.Computers and Structures，2006，84(3/4):181 －195.

［6］Cecchi A，Sab K .Out of plane model for heterogeneous periodic materials:the case of masonry［J］.Journal of Mechanics＆ Solids，2002，(21):715－746.

［7］Lotfi H R，Shing P B.Interface model applied to fracture of masonry structures［J］.Journal of Structural Engineering，1994，120(1):63－80.

［8］娄建武，龙 源，等.工程爆破中的建筑物振动监测［J］.解放军理工大学学报，2000，1(5):58－62.

［9］陈士海，逄焕东.爆破灾害预测与控制［M］.北京:煤炭工业出版社，66－82.

Safety standards discussion for blasting vibration of typical masonry buildings with dynamic finite element method

WEI Hai-xia1，2，CHEN Shi-hai2，ZHANG An-kang2

(1.School of Civil Engineering，Henan Polytechnic University，Jiaozuo 454003，Henan，China;2.College of Civil Engineering and Architecture，Shandong University of Science and Technology，Qingdao 266510，China)

A three-dimensional solid model was built for an actual three-storey masonry building in blasting filed.Measured signals of blasting seismic waves at the bottom were loaded onto the foundation base of the model，and blasting vibration responses of the other storeys calculated with dynamic finite element method were compared with the measured results.One typical structure was selected respectively among common masonry buildings of 2～4 storeys to build its finite element model，and blasting seismic waves of different dominant frequencies were loaded on its base nodes in vertical direction and the cracking course of the model was simulated.Safety standards of blasting vibration of typical masonry buildings of 2～4 storeys under blasting seismic waves of different dominant-frequency bands were given，they were obtained by defining critical failure state of structural element.The results indicated that the safety standards of blasting vibration in existing safety regulations for blasting made based on engineering experience and macro-survey data seem too gross and do not consider differences of vibration characteristics between structural individuals for one type of building;they can not be widely used because they can not guarantee the safety of all structures.

masonry building;dynamic finite element method;critical failure state;safety standards

TU311.3

A

国家自然科学基金(50778107);教育部高校博士学科点专项基金(20060424002);山东省“泰山学者”建设工程专项经费资助;土木工程防灾减灾山东省重点实验室资助

2009－07－09 修改稿收到日期:2010－03－18

魏海霞 女，博士生，1982年生