浅谈“基本不等式”在高中物理解题中的应用

汤云强

(句容市高级中学 江苏 句容 212400)

1 基本不等式

2 应用

2.1 非完全弹性碰撞

【例1】如图1所示，光滑水平面上，质量为m的物体A以速度v0与静止的物体B(质量也为m)发生对心碰撞.讨论：若为非完全弹性碰撞(动量守恒、动能有损失)，求AB后来的运动状态,及系统动能损失情况．

图1

分析：根据完全非弹性碰撞的定义，设A、B后来的速度分别为vA、vB，取v0方向为正方向，可得

(1)

(2)

将(1)式代入(2)可知

|ΔEk|=mvAvB

利用基本不等式(1)可得

2.2 等量同号电荷中垂线上电场强度极值

【例2】如图2所示，真空中有两等量同号正电荷Q，间距为L．讨论中垂线上的电场强度极值．

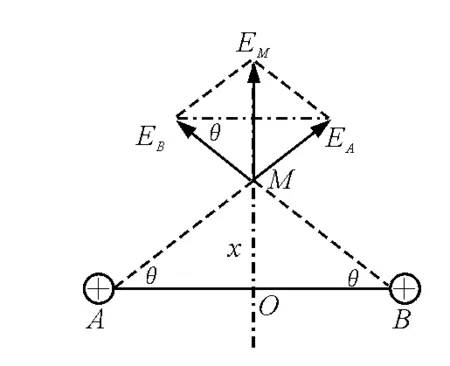
图2

分析：取中垂线上某点M,与两电荷连线夹角均为θ，由平行四边形定则可得，M点场强

令f(θ)=sinθcos2θ，得

2f2(θ)=2sin2θcos4θ=

(2sin2θ)(cos2θ)(cos2θ)

利用基本不等式(2)可得

(2sin2θ)(cos2θ)(cos2θ)≤

即当2sin2θ=cos2θ时

f(θ)有最大值

2.3 连接体的速度极值

【例3】如图3所示，滑块A、B质量均为m.A套在固定竖直杆上，A、B通过转轴用长度为L的刚性轻杆连接，B放在水平面上并靠着竖直杆．A、B均静止．由于微小扰动，B开始沿水平面向右运动．不计一切摩擦，A、B可视为质点，求在A下滑过程中B的最大速度．

图3

分析：设A下降至图4所示位置时，B达最大速度vBm，此时杆与水平方向夹角为θ．由A、B系统机械能守恒，结合连接体牵连速度的计算可知

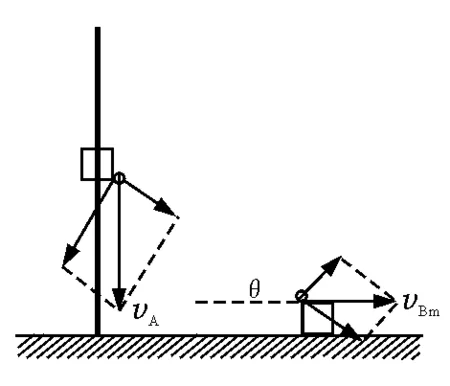
图4

可得

令f(θ)=2(1-sinθ)sin2θ=

(2-2sinθ)(sinθ)(sinθ)

利用基本不等式(2)可得

(2-2sinθ)(sinθ)(sinθ)≤

3 总结

在中学物理教学中，加强对学生进行数学方法的教育，不仅可以加深学生对物理学的基本概念、基本理论的理解，而且可以提高学生对自然规律的正确认识，培养学生的创新精神和实践能力．