基于VC++的刀具参数化CAD/CAI实现
刘 媛,段国奇
(安徽电子信息职业技术学院 电子系,安徽 蚌埠 233030)
1 问题的提出
长期以来,在讲授“刀具的几何参数及其对切削性能的影响”这部分内容的时候,由于刀具的几何角度复杂,对切削性能的影响更复杂,很难用二维图形表达清楚.如果将实物刀具拿到课堂上来,一方面很难备齐各种角度的刀具;而且有的刀具几何角度很小,不适合教学需要;此外,没有加工环境,学生很难理解刀具的角度对加工的影响.如果将虚拟实验环境引入课堂,通过输入参数化的刀具的几何角度绘制刀具,可以很好解决这一问题.以车刀为例,虚拟实验环境根据给定不同的角度值生成不同的刀具,可以使学生完全理解“三面两刃一个刀尖”以及六个基本角和两个派生角的概念.进一步可以进行虚拟切削实验,使学生深刻理解刀具的角度不同对切削温度、切屑流向、刀具寿命等的影响.采用虚拟现实技术实现的各种虚拟实验环境,可以使实验者像在真实的实验环境中一样完成各种预定的实验项目,所取得的学习或训练效果等价于甚至优于在真实环境中所取得的效果.
2 参数化工具简介
程序设计语言具有开发灵活、功能强大等优点,在机械加工领域可以和CAD/CAE/CAM等软件相结合开发出具有仿真效果的课件.虽然一次课件开发较为费力、周期较长,但是由于代码具有很强的可移植性和复用性,因而能够有效地开发智能积件.本文采用OpenGL和VC++开发刀具的参数化绘制虚拟仿真环境.OpenGL是由SGI公司发布的低层的图形软件接口(3DAPI).要编译和构件OpenGL开发的源程序,必须在Windows平台下包含以下几个图形库:基本库opengl32.lib,实用库glu32.lib,辅助库glaux.lib和实用工具库glut32.lib,同时必须在Windows的System目录下包含OpenGL提供的两个动态链接库 “opengl32.dllglu32.dll” .这些图形库一般光盘上都会附带,也可以从OpenGL的官方网站(www.opengl.org)上获取[1].
3 车刀的几何参数
以车刀为例,车刀的切削部分是刀体,它包括三面[2]:前刀面(Ar)、主后刀面(Aα)、副后刀面(Aα');两刃:一是前刀面与主后刀面相交的边锋称为主切削刃.二是前刀面与副后刀面相交的边锋称为副切削刃.一般情况,定义三个辅助平面:基面、切削平面、正交平面.车刀的切削部分的几何角度由六个基本角:主偏角(Κr)、副偏角(Κr')、前角(γ0)、后角(α0)、副后角(α0')、刃倾角(λs)和两个派生角:楔角(β0)、刀尖角(εr)来确定.其中,在基面内测量的角度有三个:一是主偏角(Κr),在基面内主切削刃与走刀方向之间的夹角.二是副偏角(Κr'),在基面内副切削刃与反走刀方向之间的夹角,它影响已加工表面粗糙度.三是刀尖角(εr),在基面内主、副切削刃之间的夹角.在正交平面内测量的角度有四个:一是前角(γ0),前刀面与基面之间的夹角.二是后角(α0),切削平面与后刀面之间的夹角.三是副后角(α0'),副切削平面与副后刀面之间的夹角.四是楔角(β0),前刀面与主后刀面之间的夹角,通常β0=90°-(γ0+α0).在切削平面内测量的角度是刃倾角(λs),为主切削刃与基面之间的夹角.
为了简化问题,将刀具看成用以下的方式形成:(1)由刃倾角做出主切削刃A1A4.(2)由主切削刃A1A3和前角γ0确定前刀面A1A4A6.(3)由主后角α0和主切削刃A1A4确定主后刀面A1A4A5.(4)由副后角α0'和副切削刃A6A4确定副后刀面A6A4A5.结果如图1所示:
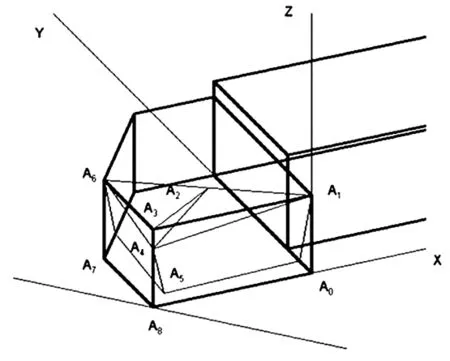
图1 车刀的形成图
4 基于OpenGL的车刀绘制的关键技术
4.1 各个点的坐标
OpenGL以多边形面片的形式绘制形体.因而,必须知道关键点的坐标,才能够按照点绘制出相应的面.首先,A0点设为原点,A0A1为Z轴方向,如图确定X轴方向和Y轴方向,∠A3A1A4为刃倾角λs,A3A2⊥A1A6,可以证明,∠A3A2A4为前角γ0,∠A6A3A1为刀尖角εr.为了简化计算,假设A3A1长度为15,由于刀尖角εr由主偏角(Κr)和副偏角(Κr')确定,前角也是参数化设定的,因而假设A3A6长度为L.可以证明,L由下式确定:
L2(sin2εrtg2γ0-tg2λs)+(30cosεrtgλs)L-225tg2λs=0,
假设A=sin2εrtg2γ0-tg2λs,B=30cosεrtgλs,C=225tg2λs,
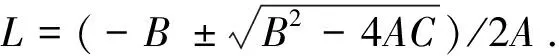
则各点坐标依次确定为:A0(0,0,0),A1(0,0,10),A3(-15,0,10),A4(-15,0,10-15tgλs),A6(-15-Lcos(90-εr),Lsin(90-εr),10).
4.2 A5的坐标
由于确定刀具形状的六个基本角难以直接在形体上表示出来[2],在这里,采用向量几何的方法确定A5点的坐标.假设A5坐标(x,y,0),主后刀面A1A4A5的法向量为:
=(-15ytgλs,15xtgλS+150,15y),

cosα0,该式可以简化为
y2+B1x2+B2x+B3=0
(1)
其中,令m=tgλs,B1=(m2-m2sec2α0)/(1+m2),
B2=(20xm)/(1+m2),B3=100/(1+m2).
类似地,副切削平面(A3A6A7A8)的法线为:
n2=A3A6×A3A4
=(15Lsin(90-εr)tgλs,15tgλsLcos(90-εr),0)
规范化为n2'=(sin(90-εr),cos(90-εr),0),
令n=Lsin(90-εr),q=Lcos(90-εr),副后刀面A6A4A5的法向量为:

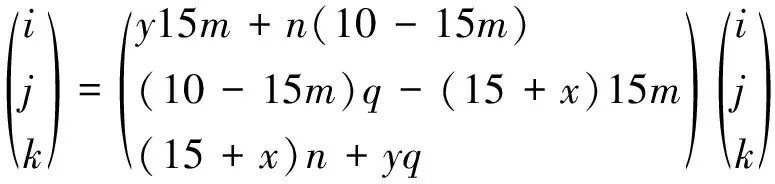
而nα0'·n2'=|nα0'|·|n2'|cosα0'因而有,
[y15m+n(10-15m)]sin(90-εr)+[(10-15m)q-(15+x)15m]cos(90-εr)=
{[y15m+n(10-15m)]2+ [(10-15m)q-
(15+x)15m]2+[(15+x)n+yq]2}1/2cosα0'
该式可以简化为:
y2+A1x2+A2x+A3y+A4xy+A5=0
(2)
其中,A1=C12/C11,A2=C13/C11,……,C4=(10-15m)q,C5=cos(90-εr),C6= cosα0',C0=(10-15m)n.虽然参数形式上很复杂,但是在VC++环境下很容易求出以上这些数值.将(1)(2)两式联立,求出x和y的值,就可以知道A5坐标(x,y,0).在具体的程序编制过程中,可以设计一个解二元二次方程组的函数fun2cifangchengzu(){},返回x和y的值.需要注意的是,这里x取负实数值,y取正实数值.[3].
4.3 绘制实例
(1)用VC++程序构建绘制数据输入界面,如图2所示.
(2)编写绘制车刀形体的程序.
①首先编写满足本文所述约束条件的计算二元二次方程的函数.
fun2cifangchengzu(……){……},
②根据输入的参数计算A1到A4各点坐标.
floatA[5][3];/三维点,共有5个A[0][0]=0,A[0][1]=0,A[0][2]=0,……
A[3][0]=-15,A[3][1]=0,A[3][2]= 10-15tgλs,……
③计算A5点坐标.
调用函数fun2cifangchengzu(){},返回x和y的值,求出A5坐标(x,y,0).
④编写绘制车刀的程序.
在OpenGL下,绘制的有关程序如下:
glBegin(GL_TRIANGLES);// 绘制A1A4A6面
glNormal3f(0.0f, 0.0f, 1.0f);// 法线方向朝Z轴正向
glVertex3f(0,0,10);//A1点的坐标
glVertex3f(-15,0,10-15tgλs);//A4点的坐标
glVertex3f(-15-Lcos(90-εr),Lsin(90-εr),10); //A6点的坐标……//做出其它面,形成刀具的各个面.
绘制面的时候,要给定法线的方向,开启光照以后,就可以按照输入参数值绘制出具有真实感的刀具的形状.
⑤编译构建和运行.
编译构建形成可执行文件以后,双击运行.出现对话框,输入数据,如图2所示.
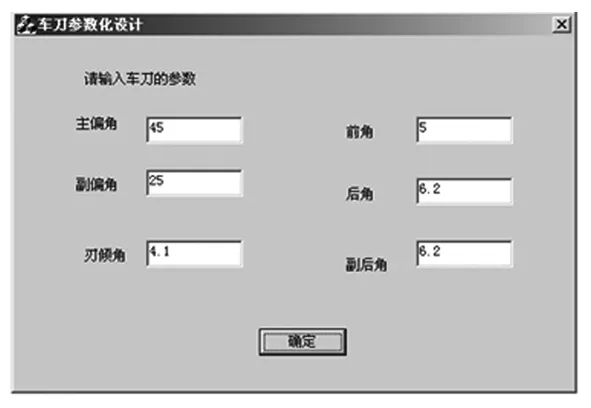
图2 输入刀具参数界面
单击确定,绘制出如图3所示图形:

图3 参数化车刀模型
参数化车刀模型在车工工艺学课程教学中的优势为可以很方便的得到不同角度的各种车刀.例如,上例中我们只要在界面中的输入新参数,点击确定以后就可以绘制出一个新的车刀模型.我们还可以改变观察方向,以便从不同的方向观察理解图形.如图4所示是前角为正5°后角为6.2°的车刀;如图5所示是前角为负5°后角为5.8°的车刀,可以方便学生更好地理解主偏角、副偏角、前角、后角、楔角等概念.

图4 前角为正的车刀

图5 前角为负的车刀
5 总结
在传统讲授“刀具的几何参数及其对切削性能的影响”的教学模式中,学生学习兴趣较低,知识枯燥难懂,致使很多学生厌学,效果不佳.应用上例实践的刀具参数化的方法可以使刀具形象具体,教师能够根据自己的教学内容快速生成不同几何参数的刀具,方便教师讲解和学生观察理解,特别适合目前教学环境,能收到很好的效果.
[1]李胜睿,等.计算机图形学实验教程[M].北京:机械工业出版社,2004.
[2]王琳,等.机械加工通用基础知识[M].北京:中国劳动和社会保障出版社,2003.
[3]简明数学手册[M].上海:上海教育出版社,1978.

