时滞Holling-III型捕食系统的稳定性
庄科俊(1.安徽财经大学统计与应用数学学院,安徽蚌埠233030;2.安徽财经大学应用数学研究所)
时滞Holling-III型捕食系统的稳定性
庄科俊1,2
(1.安徽财经大学统计与应用数学学院,安徽蚌埠233030;2.安徽财经大学应用数学研究所)
文中研究了一类具有时滞的捕食者-食饵系统正平衡点的稳定性,给出了产生Hopf分支的充分条件.关键词:捕食者-食饵系统;Hopf分支;稳定性;时滞
1 引言
近年来,对具有时滞和功能响应的捕食者-食饵系统周期解的研究,引起了极大的关注,并且得到了一些很好的结果,参见文献[1-3].本文主要考虑基于比率的Holling-III型捕食系统:

这里N1(t)与N2(t)分别表示食饵种群与捕食种群的密度,系统中各系数均为正常数,b1表示食饵种群的内禀增长率,b2表示捕食者种群的死亡率,α1与α2分别表示相应的转化率,m表示半捕获饱和度.并且τ非负,表示捕食种群的成熟时滞.在没有捕食者的情况下,食饵种群遵循Logistic增长规律.
对于系统(1),文献[1-2]主要研究了周期解的全局存在性及稳定性,而文献[3]则考虑其对应的离散系统的周期解.受文献[1,4]的启发,我们主要以时滞τ为参数,讨论系统(1)正平衡点的稳定性及Hopf分支的存在性,进而得到系统存在小振幅周期解的充分条件.
2 正平衡点的稳定性与周期解的存在性
为了简便,首先作如下假设:

(H3)a11+a22<0且a11a22-a12a21>0.
定理1若(H1)与(H2)成立,则系统(1)有唯一的正平衡点.
证明系统(1)的平衡点(N1,N2)满足方程组

考虑到生态模型的实际意义,下面主要考虑正平衡点的有关性质.系统(1)在正平衡点(N*1,N*2)处的线性近似系统为:
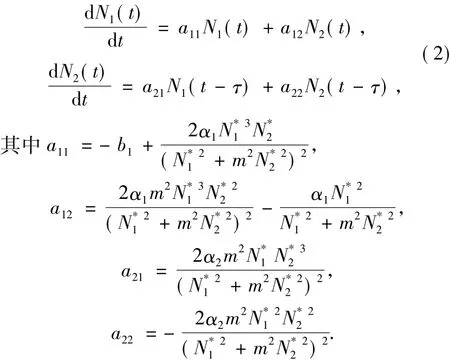
则系统(2)对应的特征方程为:
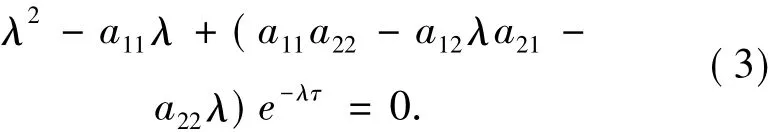
引理1当τ=0时,如果(H3)成立,则方程(3)的根都具有严格负实部.
引理2如果(H3)成立,则方程(3)当τ=τj时,有且仅有一对纯虚根±iω0,其中

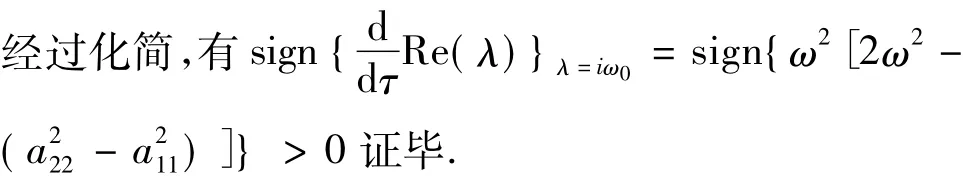
根据文献[5]中的推论2.4,指数多项式的零根随参数的变化而出现在或穿过虚轴时,具有正实部的零根总数才会发生改变,从而可以得到特征根的分布情况.
引理4如果(H1)-(H3)成立,则当t∈[0,τ0)时,方程(3)的所有根都具有严格负实部;当τ =τ0时,方程(3)除有一对纯虚根±iω0外,其它根都具有严格负实部;当τ∈(τj,tj+1]时,方程(3)有2(j+1)个具严格正实部的根.
综合引理1-4及Hopf分支定理[6],我们有如下关于系统(1)的稳定性和分支周期解的存在性定理.
定理2对系统(1),如果(H1)-(H3)成立,则当t∈[0,τ0)时,系统(1)的正平衡点是渐近稳定的;当τ>τ0时,系统(1)的正平衡点不稳定;τ= τ0是系统(1)的Hopf分支值,即在τ0的右侧小邻域内,系统(1)从正平衡点附近分支出小振幅的周期解.
3 结论
由主要定理可以知道,时滞τ的改变可以导致系统(1)的不稳定性,在一定条件下,若捕食种群的成熟时滞较小,种群数量达到静态的平衡;当该时滞较大时,两种群的数量将呈周期变化,达到动态的平衡.此外,由于系统(1)的形式比较复杂,对正平衡点的稳定性及局部Hopf分支存在性的研究已经比较困难,关于Hopf分支的全局延拓,还有待于进一步的讨论.
[1]Wang Linlin,LiWantong.Existence of periodic solutions of a delayed predator-prey system with functional response[J].Int JMath Sci,2002,1 (1-2):55-63.
[2]Wang Linlin,LiWantong.Existence and global stability of positive periodic solutionsofa predator-prey system with delays[J].ApplMath Comput,2003,146(1):167-185.
[3]Wang Linlin,LiWantong.Periodic solutions and stability for a delayed discrete ratio-dependent predator-prey system with Holling-type functional response[J].Discrete Dynamics in Nature and Society,2004(2):325-343.
[4]Zhuang Kejun,LiXiangao,Li Zunxian.Local and global Hopf bifurcations for a predator-prey system with two delays[J].Ann Diff Eqs,2006,22 (3):483-486.
[5]Ruan Shigui,Wei Junjie.On the zeros of transcendental functionswith applications to stability of delay differential equationswith two delays[J].Dyn Cont Disc Impuls Syst,2003(10):863-874.
[6]Hassard B D,Kazarinoff N D,Wan Y H.Theory and applications of Hopf bifurcation[M].Cambridge:Cambridge University Press,1981.
(责任编辑:王宏志)
Q141
A
1008-7974(2011)02-0017-02
安徽省青年科学基金项目(10040606Q01).
2010-10-10
庄科俊(1982-),江苏金坛人,硕士,安徽财经大学统计与应用数学学院讲师.

