最大度为5不含6-圈的可平面图的边染色
,,
(中国矿业大学 理学院,江苏 徐州 221008)
0 引言
本文考虑的图都是简单的无向有限图.分别用V(G),E(G),F(G),Δ(G)(简记为Δ)表示一个平面图G的点集,边集,面集,最大度.用dk(v)表示点v的度数为k的邻点的个数,dk+(v)表示点v的度数不小于k的邻点的个数.G中任意两个圈(或面),如果它们至少有一条重边,则称为相邻的;G中的任意两个圈(或面),如果它们关联于同一个顶点,则称为相交的.若存在一个映射φ:E(G)→{1,2,…,k},对G中任意两条相邻接的边e1和e2,有φ(e1)≠φ(e2),则称G是k-边可染色的,使得图G具有k-边可染色的最小的正整数k定义为G的边色数,记作χ′(G).若图G满足χ′(G)=Δ(G)称G为第一类图,若χ′(G)=Δ(G)+1称G为第二类图.若图G是连通的第二类图,并且去掉任意边e∈G后,G-e是第一类图,则称G是一个临界图.
Vizing[1,2]证明了6≤Δ≤7的简单平面图是第一类的.时隔30多年,文[3,4]分别独立证明了平面图猜想对Δ=7是正确的.文[5,6]给出了Δ=6的可平面图是第一类图的充分条件.对于Δ=5的可平面图,文[7]证明了,Δ=5且围长不小于4的可平面图是第一类图.文[8]证明了最大度为5,不含四圈且不含五圈的平面图是第一类的.文[9]证明了Δ=5且没有相交三角形的可平面图是第一类图.文[10]证明了最大度为4是第一类图的一些充分条件.笔者将证明:Δ=5且没有六圈的简单平面图是第一类的.
1 临界图的性质
引理1[2]设G是一个Δ-临界图且v∈V(G),那么
1)v至少相邻2个Δ-点;
2)如果dk(v)≥1,k≠Δ,则dΔ(v)≥Δ-k+1.
引理2[4]设G是一个Δ-临界图,xy∈E(G)使得d(x)+d(y)=Δ+2,那么
1)每个v∈N(x,y){x,y}是Δ-点;
2)每个v∈N(N(x,y)){x,y}满足d(v)≥Δ-1;
3)如果d(x)<Δ,d(y)<Δ,则每个v∈N(N(x,y)){x,y}是Δ-点.
引理3[3]如果G包含3个不同的点s,t,w满足下列两个条件,那么G不是一个Δ-临界图;
1)t,w∈N(s),且d(w)<2Δ-d(s)-d(t)+2;
2)sw含在至少d(s)+d(t)-Δ-2个三角形中,且t不是这些三角形的顶点.
2 主要结果
定理Δ=5且没有六圈的简单平面图G是第一类的.
证明假设定理不成立,即G是第二类图.不失一般性,可以假设G是5-临界简单图,那么G显然是2-连通的.因此G的每个面的边界是一个圈,且每条边位于2个不同面的边界上.由Euler公式进行简单变换可得
对于任意x∈V(G)∪F(G),定义x的权初值ch(x)为
下面根据给出的权转移规则(Discharging rules),对每一个x∈V(G)∪F(G)的ch(x)进行调整,从而得到新的初值ch′(x).因为权转移之后始终保证不影响其和式的值,所以有
如果可以证明对于每一个x∈V(G)∪F(G),都有ch′(x)≥0,则与上式矛盾,从而定理得证.
定义权转移规则如下:

(R2)设x,y,z是3-面f的三个不同顶点,且d(x)≤d(y)≤d(z);
(R2-1)若f是(k,5,5)-面,其中k=2,3,4,则y,z分别分值2给f;
(R2-2)若f是(3,4,5)-面,则y,z分别分值2给f;

(R3)设f是4-面;
(R3-1)若f是(k,5,5,5)-面,其中k=2,3,4,则每个5-点分别分值1给f;

(R3-3)若f是(3,4,5,5)-面,则每个4-点和5-点分别分值1给f;

(R4)设f是5-面;



(R6)若5-点v同时关联着(3,4,5)和(3,5,5)-面或同时关联着两个(3,5,5)-面时,则其中3-点不能再关联5-面,至多关联一个4-面,所以此时v从3-点得到1;
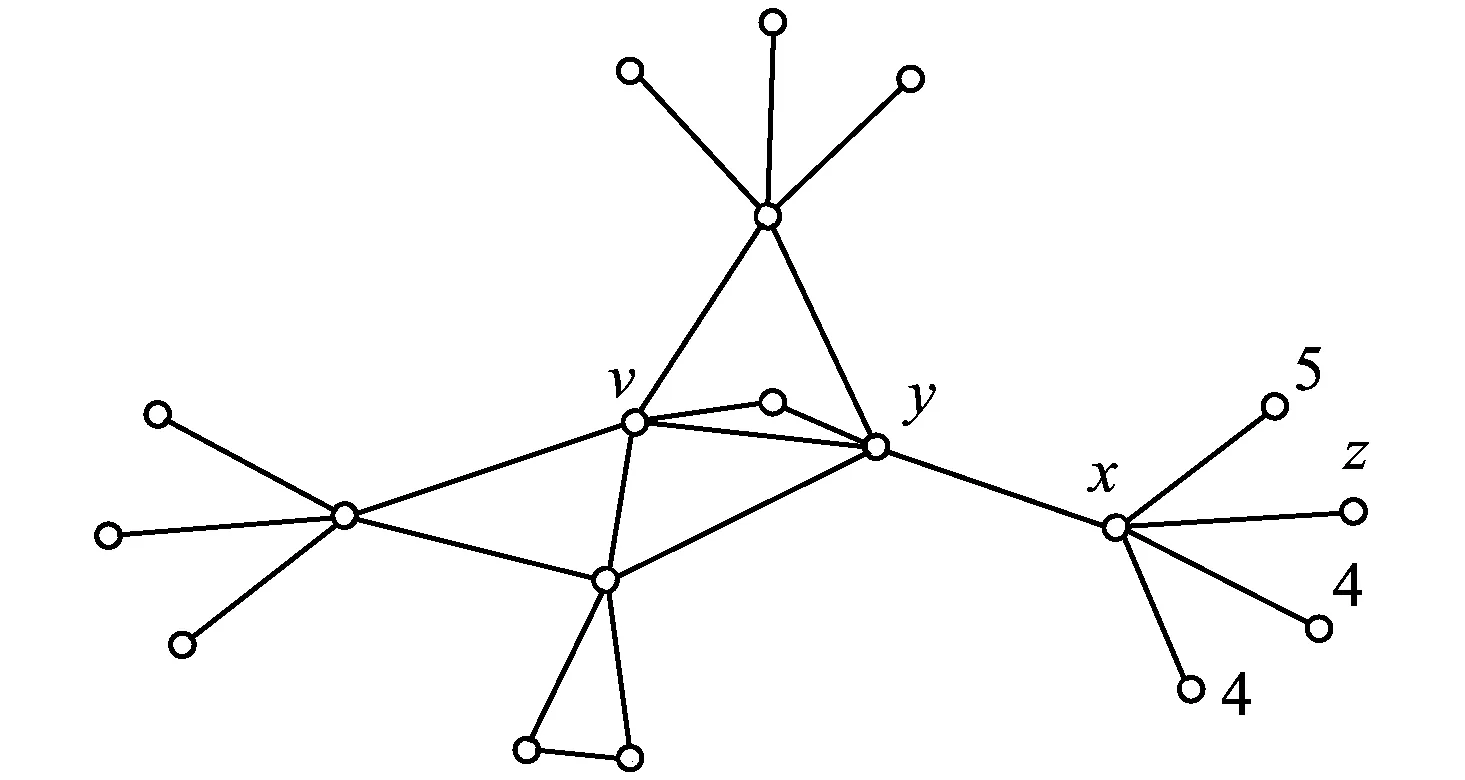
图1 2-点临界图


设f是一个度为3的面,则ch(f)=-4.由引理1,2可知,图G中度为3的面必定是1个(2,5,5),(3,4,5),(3,5,5),或(4+,4+,4+)-面.因此根据R2和R5可得ch′(f)=-4+4=0.
设f是一个度为4的面,则ch(f)=-3.由引理1,2,3可知,f必定是一个(2,5,5,5),(3,3+,5,5)或(4+,4+,4+,4+)-面.因此,根据R3可知,它的各个关联顶点恰好分值3给f,使得ch′(f)=-3+3=0
设f是一个度为5的面,则ch(f)=-2.由引理1,2,3可知,f必定是一个(2,5,5,5,5),(3,3+,5,5,5),(3,4,5,5,5),或(4+,4+,4+,4+,4+)-面.因此,根据R4可知,它的各个关联顶点至少分值2给f,使得ch′(f)=-2+2=0.

设v是一个度为2的顶点,则ch(f)=-2,由引理1可知,v的两个邻点的度均为5.因此ch′(f)=-2+1×2=0

设v是一个度为4的顶点,则ch(f)=3.通过比较R2,R3,R4可知v分值给3-面总比4-面多,v分值给4-面总比5-面多,所以在下面讨论的时候,尽量使v关联更多的3-面和4-面.

情况2 若v与两个4-点相邻,则v的另外两个邻点必是5-点.因为v只给(4,4,4)-面和(4,4,5)-面分值,所以考虑v关联尽可能多的这两个面.

情况3 若v与一个4-点,三个5-点相邻,则v可能关联(4,4,5)-面和(4,5,5)-面,且v只给(4,4,5)-面分值.



情况5 若v与2-点相邻,则v还与4个5-点相邻.


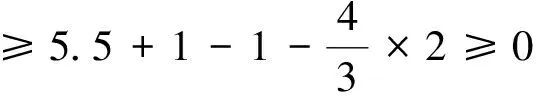
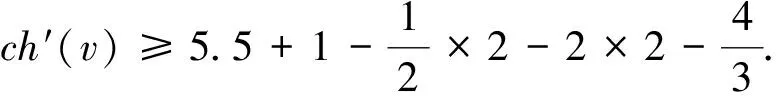



综上所述,当G中不含六圈的时候,对于任意的x∈V(G)∪F(G),都有ch′(x)≥0,这就证明了该定理.
[1]Vizing V G.On an estimate of the chromatic index of a p-graph[J].Diskret Analiz,1964,3(1):25-30.
[2]Vizing V G.Critical graphs with given chromatic class[J].Diskret Analiz,1965,5(1):9-17.
[3]Sanders D P,Zhao Y.Planar graphs of maximum degree seven are class 1[J].Combin Theory Ser B,2001,83(2):201-212.
[4]Zhang L M.Every planar with maximum degree 7 is of class 1[J].Graphs Combin,2000,16(4):467-495.
[5]Zhou G F.A note on graphs of class 1[J].Discrete Math,2003,262(1-3):339-345.
[6]Bu Y H,Wang Weifan.Some sufficient conditions for a planar graph of maximum degree six to be class 1[J].Discrete Math,2006,306(13):1440-1445.
[7]Li X C,Luo R.Edge coloring of embedded graphs with large girth[J].Graphs Combin,2003,19(3):393-401.
[8]周正同,苗连英.最大度是5的可平面图是第一类的充分条件[J].山东大学学报:自然科学版,2010(04):24-27.
[9]陈永珠,王维凡.第一类平面图的一个充分条件[J].浙江师范大学学报:自然科学版,2007(4):416-420.
[10]倪伟平.最大度是4的可平面图是第一类的充分条件[J].华东师范:自然科学版,2010(3):85-91.

