变分迭代法求解分数阶自治常微分方程

徐宇锋

(中南大学 数学科学与计算技术学院，湖南 长沙 410083)

20世纪90年代以来，普通导数意义下的微分方程和分数阶导数意义下的微分方程由于在流体力学、粘弹性力学、生物学、物理学和其他工程领域得到了广泛的应用而备受关注，研究各类物理问题中出现的微分方程的解法和解的物理意义成为了一个热点问题[1-15].许多非线性问题本身不存在解析解，所以必须使用有效的数值方法对它们进行求解.变分迭代法[3-6]是相对较新的求解微分方程的方法，它们可以在不对方程进行线性化和离散化的前提下，给出方程的极限形式的解析近似解，同时对这个极限进行高阶逼近即可得到近似数值解.

变分迭代法已经成功地运用到求解大量的线性和非线性微分方程[1-6,10-15].何吉欢[3-6]发展了变分迭代法并成功的运用到求解分数阶微分方程，Zaid Odibat[1-2]和Shaher Moman[10-15]将变分迭代法由线性微分方程推广至非线性偏微分方程，以及分数阶微分方程的求解.本文将变分迭代法应用于求解自治常微分方程组和分数阶常微分方程组的初值问题，通过数值实例验证了变分迭代法所求得的解的收敛性，及其迭代序列的后验误差的收敛性.

1 基本定义

分数阶导数是普通整数阶导数的推广，在实际的物理问题中，采用分数阶导数的微分方程模型往往可以更精确地描述客观事实.下面给出分数阶导数的定义.

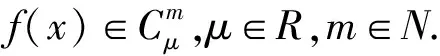
定义2 函数f(x)的α阶Riemann-Liouville分数阶积分算子定义如下：

(1)

其中：f(x)∈Cμ,μ+1≥0.

在研究中人们发现运用Riemann-Liouville导数意义下的微分方程在刻画实际物理模型时有相当的缺陷[16]，因此，Caputo在他的粘弹性理论中提出了Caputo意义下的导数弥补这些缺陷.

定义3 函数f(x)的α阶Caputo意义下分数阶微分算子定义如下：

(2)

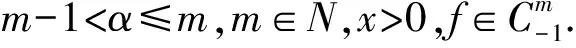
有关分数阶积分算子和微分算子的更多性质，请参阅文献[16].

2 变分迭代法的基本原理

变分迭代法的基本原理及其在各类微分方程中的应用见文献[1,3-6,10-15].以如下的常微分方程初值问题为例，给出其变分迭代法的具体求解步骤.

(3)

其中：D是微分算子，可以是Caputo意义下的分数阶微分算子，也可以是普通意义下的整数阶微分算子.与式(3)相应的初始条件为:

(x1(0),x2(0),…,xn(0))=(c1,c2,…,cn).

(4)

首先构造式(3)的惩罚泛函迭代格式：

(5)

其中：λ1(t),λ2(t),…,λn(t)是广义Lagrange乘子，可以通过下面的初值问题确定，

λi′(τ)|τ=t=0,i=1,2,…,n,

1+λi(τ)|τ=t=0,

(6)

因此得到λ1=λ2=…=λn=-1，将乘子代入式(5)中，就得到了式(3)的变分迭代格式，初始迭代值就是初值式(4)，

(7)

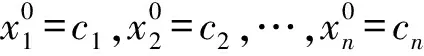
(8)

有关变分迭代法的收敛性的证明，请参阅文献[17-19]，有关迭代法的收敛性进一步结论请参阅参考文献[20-23].

3 数值实验

本节将研究两个具体的常微分方程组，利用MATLAB进行仿真，给出它们的解析解或近似解及其后验误差结果.

例1 考虑如下的线性常微分方程组：

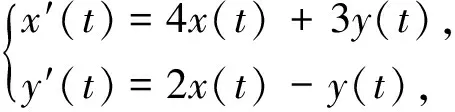
(9)

在初始条件x(0)=1,y(0)=-1下的解.

根据式(5)至式(7)的讨论，与式(9)相应的变分迭代格式为：

(10)

将初始值x0(t)=1,y0(t)=-1代入式(10)进行迭代，则得到：

(11)

继续迭代下去，得到：

容易看到，x(t)和y(t)的迭代结果收敛到式(9)的解析解：

(12)

例2 考虑如下的带Caputo型导数的分数阶非线性常微分方程组：

(13)

在初始条件x(0)=1,y(0)=2下的解，其中0<α1≤1,0<α2≤1.

根据式(5)至式(7)的讨论，与式(13)相应的变分迭代格式为：

(14)

将初始值x0(t)=1,y0(t)=2代入(14)进行迭代，则得到：

(15)

继续做下去，xk(t)和yk(t)的迭代序列将收敛到(13)的解.图1和图2给出了xk(t)和yk(t)第二次迭代和第三次迭代的相图，图3和图4给出了xk(t)和yk(t)的每次迭代序列的后验误差变化曲线，可以看到误差稳定在一定的范围.

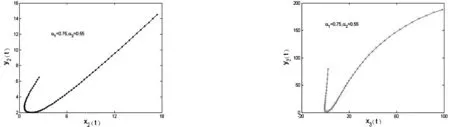
图1 第二次迭代的相图 图2 第三次迭代的相图Fig.1 Phase portrait of the second iteration Fig.2 Phase portrait of the third iteration

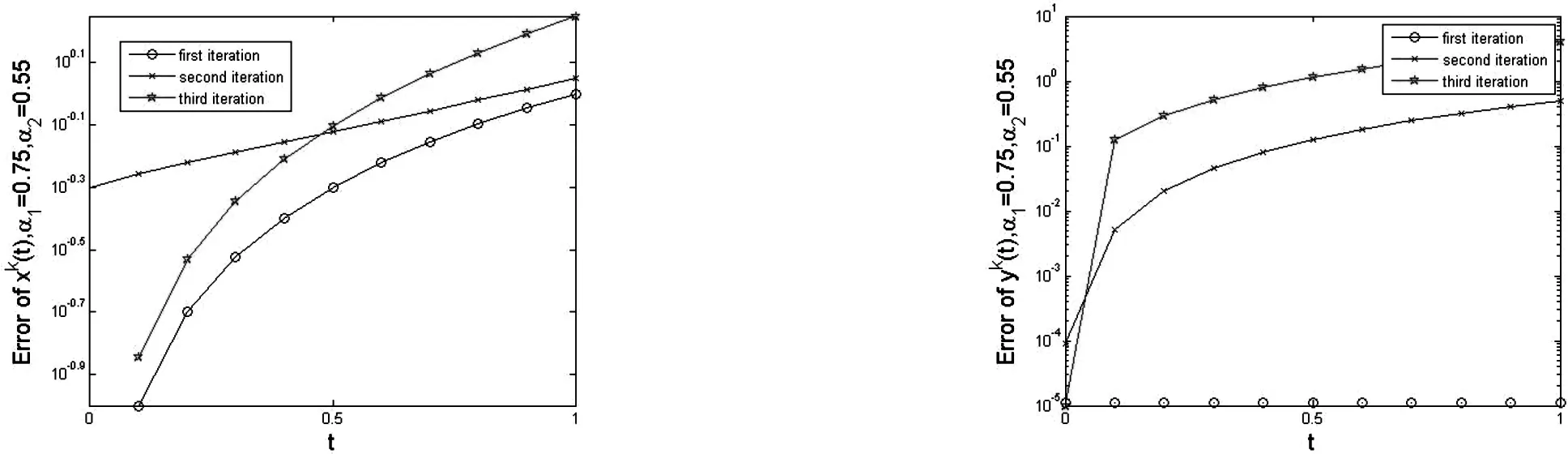
图3 xk(t)的后验误差变化 图4 yk(t)的后验误差变化Fig.3 Posteriori error of xk(t) Fig.4 Posteriori error of yk(t)

4 主要结论

本文的主要目的是将变分迭代法(VIM)应用到求解自治常微分方程组和带有Caputo型导数的分数阶自治常微分方程组，获得其解析解或者近似解.第一，数值实验表明VIM对自治常微分方程组的求解非常有效，少量的迭代即可以获得精度很高的解，对于存在解析解的自治常微分方程组，VIM的迭代序列将收敛到方程组的解析解；第二，数值实验中VIM在求解自治常微分方程组中得到的结果与解析解的泰勒展开式很好的吻合，每进行一次迭代，误差为泰勒展式的高阶余项；第三，在带Caputo型导数的常微分方程组中，VIM得到的序列收敛的解虽然表达式复杂，但是每步迭代的后验误差都稳定在一定范围，误差主要来源于计算分数阶导数时要计算大量的奇异积分；第四，作为几乎程序化的求解步骤，VIM方便利用计算机对更为复杂的微分方程进行求解，不仅可以处理Caputo型的分数阶导数，还可以利用高精度积分方法处理其他类型的任意阶的分数阶导数；最后，利用MATLAB软件给出了后一个例子的两次迭代的相图及两个分量迭代序列的后验误差变化图，可以看到误差稳定在一定的范围，说明数值实验的求解结果是有效的.

[1] Odibat Z,Momani S.Application of variational iteration method to nonlinear differential equations of Fractional order[J].Int J Nonlinear Sci Numer Simul,2006,17:15-27.

[2] Momani S,Odibat Z.Analytical solution of a time-fractional Navier-Stokes equation by Adomian decom position method[J].Appl Math Comput,2006,177:488-494.

[3] He J H.Variational iteration method for delay differential equations[J].Commun Nonlinear Sci Numer Simul,1997,2:235-236.

[4] He J H.Approximate analytical solution for seepage flow with fractional derivatives in porous Media[J].Comput Methods Appl Mech Engrg,1998,167:57-68.

[5] He J H.Variational iteration method-a kind of non-linear analytical technique:some examples[J].Int J Nonlinear Mech,1999,34:699-708.

[6] He J H.Variational iteration method for autonomous ordinary differential systems[J].Appl Math Comput,2000,14:115-123.

[7] Adomian G.A review of the decomposition method in applied mathematics[J].J Math Anal Appl,1988,135:501-544.

[8] Adomian G.Solving Frontier Problems of Physics:The Decomposition method[M].Boston:Kluwer Academic Publishers,1994.

[9] Repaci A.Nonlinear dynamical systems:on the accurancy of Adomian decomposition method[J].Appl Math Lett,1990,3:35-39.

[10] Zaid Odibat,Shaher Momani.Numerical methods for nonlinear partial differential equations of fractional order[J].Appl Math Mode,2008,32:28-39.

[11] Shaher Momani,Zaid Odibat.Numerical approach to differential equations of fractional order[J].J Com Appl Math,2007,207:96-110.

[12] Momani S.Non-perturbative analytical solutions of the space- and time-fractional Burgers equation[J].Chaos Solitons fractals,2006,28:930-937.

[13] Momani S.Odibat Z,Numerical comparison of methods for solving linear differential equations of fractional order[J].Chaos Solitons Fractals,2007,31:1248-1255.

[14] Momani S,Abuasad S.Application of He's variational iteration method to Helmholtz equation[J].Chaos Solitons Fractals,2006,27:1119-1123.

[15] Momani S.An explicit and numerical solutions of the fractional KdV equation[J].Math Comput Simul,2005,70:110-118.

[16] Podlubny I.Fractional Differential Equations[M].San Diego:Academic Press,1999.

[17] Zaid Odibat.A study on the convergence of variational iteration method[J].Math Compu Model,2010,51:1181-1192.

[18] Salkuyeh D K.Convergence of the variational iteration method for solving linear systems of ODEs with constant coefficients[J].Comp Math Appl,2008,56:2027-2033.

[19] Tatari M,Dehghan M.On the convergence of He's variational iteration method[J].J Comp Appl Math,2007,207:121-128.

[20] Huang Z Y,Noor M A.Equivalency of convergence between one-step iteration algorithm and two-step iteration algorithm of variational inclusion for H-monotone mappings[J].Comp Math Appl,2007,53:1567-1571.

[21] Song Y S,Zheng Y C.Strong convergence of iteration algorithms for a countable family of nonexpansive mappings[J].Nonlinear Analysis,2009,71:3072-3082.

[22] Saadati R,Dehghan M,Vaezpour S M,et al.The convergence of He's variational iteration method for solving integral equations[J].Com Math Appl,2009,58:2167-2171.

[23] Nammanee K,Noor M A,Suantai S.Convergence criteria of modified Norr's iterations with errors for asymptotically nonexpansive mappings[J].J Math Anal Appl,2006,314:320-334.