基于分幅切割方法的基本农田图像精确纠正

张 沛，陈朝晖

(1.南宁市国土资源局,广西 南宁 530021;2.南宁市国土资源信息中心，广西 南宁 530021)

由扫描得到的栅格图像其坐标基于扫描仪的坐标系统，而第二次全国土地调查要求成果数据统一采用1980西安坐标系，因此在对基本农田扫描图像数字化前要先对其进行纠正，使其具有第二次全国土地调查要求的统一地理坐标系统.基本农田扫描图像纠正要在图像和1∶10 000地形图上选择相应的控制点，然后通过建立的数学模型对扫描图像进行纠正.采用的纠正方法和控制点数量与精度直接影响着纠正的质量.

本文在分析基本农田图像误差来源的基础上，提出采用分幅切割的方法对基本农田图像进行精确纠正的思路，并就纠正的结果与其他几种常用的纠正方法进行了误差比较.

1 现有资料分析

南宁市(1997-2010)基本农田保护区分布图是2001年在1∶10 000标准分幅土地利用现状薄膜图和1∶10 000地形图的基础上，根据原国家土地管理局、农业部制定的《划定基本农田保护区技术规程(试行)》和1998年12月27日国务院令第257号发布的《基本农田保护条例》相关要求，以出图表示为主要目的、乡镇为基本单元制作而成的.

由于历史的原因和当时应用要求的问题，这些资料普遍存在以下问题：

1)没有采用统一的坐标系.图件制作时由于仅考虑了出图表示的需要而全部采用了自由坐标系，虽然每幅图上都标示有坐标网格，但只是为了出图，标示的坐标值并不准确，误差较大，没有实际参考作用.同时由于没有采用统一的坐标系，且相邻乡镇之间没有做好接边工作，导致相邻乡镇的图件存在相互重叠和错位，拼接后出现非常大的重叠或空隙.

2)数据格式不统一.由于基本农田图件的制作单位有多家，而每家单位使用的软件都不一样，造成图件数据格式不统一.这些图件格式有MapInfo、MapGIS、AutoCAD、手工制作图几种.每种格式的数据分层都比较混乱，难以采用自动化手段完成原始数据的整理.

3)比例尺不统一.各县级、乡镇级基本农田图件采用的比例尺多样，有1∶10 000、1∶18 000、1∶20 000、1∶25 000等，比例尺从1∶10 000～1∶50 000不等，且有的不是国家基本比例尺.

4)整图相对精度极差.基本农田图件是在1∶10 000标准分幅土地利用现状图和地形图的基础上制作的，在单个图幅内其精度满足1∶10 000比例尺的要求.但在制作乡镇级、县级基本农田图件时，需要将多个图幅的数据进行拼接.由于没有将各图幅的数据统一到一个坐标系下，造成各分幅图拼接成乡镇图后整图的相对精度极差.按传统的方法纠正，都只能达到局部精度能满足要求[1-2]，其余部分误差却很大，往往顾此失彼，无法得到较好的整图纠正效果，其整图纠正精度仅有±100 m.

2 基本农田图像纠正

2.1 纠正采用的基础图件资料

基本农田栅格图像纠正采用的基础资料主要包括：①GeoTiff格式的1∶10 000标准分幅地形图，主要用于基本农田保护区分布图的纠正和精度检查.②Tiff格式乡镇基本农田保护区分布图，分辨率为300 dpi.③80坐标系DGN格式的1∶10 000乡镇级行政区划图，为基本农田图像的粗纠正提供参考.④80坐标系1∶10 000标准分幅接图表，为基本农田图像的分幅切割提供参考.

2.2 基本农田图像预处理

1)统一图像分辨率

由于基本农田图件的数据格式、比例尺都不统一，为此首先以乡镇为单位将不同格式的基本农田图件进行栅格化，像素分辨率统一在1∶10 000比例精度，即1 m/像素.

2)基本农田图像的粗纠正

为提高纠正时采集控制点的效率，将TIFF格式基本农田保护区分布图转入Bentley Descartes图像纠正软件中，以80坐标系乡镇行政区划图为参照，每幅图像采集2个控制点，使用矩形纠正方法进行粗纠正.

3)基本农田图像的整体纠正

基本农田图像的整体纠正是在Bentley Descartes软件中，以配准好的1∶10 000扫描地形图作为参照，按所选择的纠正方法对控制点数量的要求，在经过粗纠正的基本农田图像上选取足够数量且均匀分布的控制点，对其进行整体纠正.

4)采用仿射变换纠正方法

仿射变换用于修正两图像间的关于旋转、缩放、以及平移的相对差异.仿射变换公式[3]可表示为：

仿射变换纠正需要的控制点个数最少为3个，本次纠正选取了 5个均匀分布的控制点，控制点的选取分布情况如图1所示.

5)采用二阶多项式纠正方法

二阶多项式公式变换公式可表示为：

二阶多项式纠正需要的控制点个数最少为6个[4]，本次纠正选取了 10个均匀分布的控制点，控制点的选取分布情况如图2所示.

图1 仿射变换纠正控制点 图2 二阶多项式纠正控制点Fig.1 Affine transformation to correct the control point Fig.2 Second-order polynomial to correct the control point

6)采用三阶多项式纠正方法

三阶多项式公式可表示为：

X=a0+a1·x+a2·y+a3·xy+a4·x2+a5·y2+a6·x2y+a7·xy2+a8·x3+a9·y3

Y=b0+b1·x+b2·y+b3·xy+b4·x2+b5·y2+b6·x2y+b7·xy2+b8·x3+b9·y3

三阶多项式纠正需要的控制点个数最少为10个，本次纠正选取了 16个均匀分布的控制点，控制点的选取分布情况如图3所示.

7)采用基于Thin Plate Spline模型的局部区域纠正方法

局部区域[5-7]纠正方法采用分段多项式(piecewise polynomials)函数建立待纠正图像和参考图像间的变换关系.它的基本原理是以采集的控制点为顶点，将参考图像进行区域的三角化划分，然后在待纠正图像中识别对应的三角化区域，在每一对对应的三角区域中，定义Thin Plate Spline局部变换函数对图像进行变换.Thin Plate Spline函数可用如下公式表示：

局部区域纠正需要的控制点个数最少为4个，本次纠正选取了 20个均匀分布的控制点，控制点的选取分布情况如图4所示.

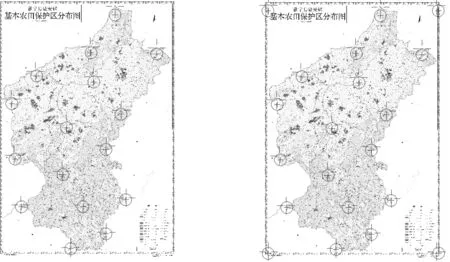
图3 三阶多项式纠正控制点 图4 局部区域纠正控制点Fig.3 Third order polynomial to correct the control point Fig.4 Local area control points to correct

2.3 基本农田图像的分幅切割精确纠正

从基本农田图件存在的问题分析结果可以看出，虽然图件的整图相对精度极差，但在单个图幅内，其精度是满足1∶10 000比例尺精度要求的.因此只有先将基本农田图像按1∶1图幅范围进行切割分幅，然后再分别对各分幅图像进行纠正，这样才能消除图件制作过程中因拼接分幅图而造成的整图误差.

2.3.1 分幅切割精确纠正基本思路 基本农田图像的分幅切割精确纠正的基本思路为：将经过粗纠正的各乡镇基本农田图像按1∶10 000标准分幅进行切割，然后参考地形图选取控制点，对分幅的基本农田图像采用2阶多项式纠正方法进行精确纠正，最后将纠正完成的分幅基本农田图像进行合并，得到经过精确纠正的乡镇基本农田图像.图5是整个分幅切割精确纠正的流程.

2.3.2 基本农田图像的分幅切割 以80坐标系的1∶10 000标准分幅接合图为参考，对每幅经过粗纠正后的乡镇基本农田图像按大于1∶10 000标准分幅200 m的大小进行分幅切割，为后续的分幅几何精确纠正做准备.之所以按稍大于标准图幅的范围进行切割，是为了保证相邻图幅图像间有一定的重叠度，这样分幅的图像在完成纠正后能够重新拼接成一幅完整的乡镇基本农田图像[8].图6为基本农田分幅切割示意图，其中黑色虚线为切割范围线.

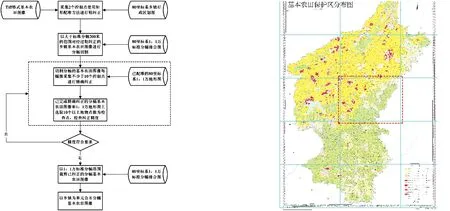
图5 基本农田分幅切割精确纠正流程图 图6 基本农田分幅切割 Fig. .5 Accurate cutting of basic farmland framing correct flow Fig.6 The basic farmland amplitude cutting

2.3.3 选取控制点 为保证控制点的精度，根据基本农田图像的特点，在采集控制点的过程中，主要选取位于山沟的条带状基本农田图斑中心点、等高线中的计曲线、道路交叉点等标志性地物特征点等，且保证控制点要均匀分布，数量在10个左右.

2.3.4 基本农田分幅图像的精确纠正 控制点采集完成后，选用2次多项式(Polynomial)纠正方法对分幅基本农田图像进行精确纠正.由于各分幅的基本农田图像变形并不大，而高阶多项式变换在使纠正图像与参考图像配准过程中很容易使远离控制点的区域产生较大偏差[9-10]，因此对分幅的基本农田图像纠正时选用了2次多项式纠正方法.

2.3.5 合并已精确纠正的基本农田分幅图像 在Bentley Descartes软件中使用光栅参考工具，以乡镇为基本单元，将已完成精确纠正的分幅基本农田图像连接到当前工作文件中，然后参考1∶10 000标准分幅接合图，以1∶10 000标准图幅范围对每幅基本农田图像进行剪切.最后使用光栅合并工具，将分幅的基本农田图像进行合并，得到完整的乡镇基本农田图像.

3 纠正结果精度分析

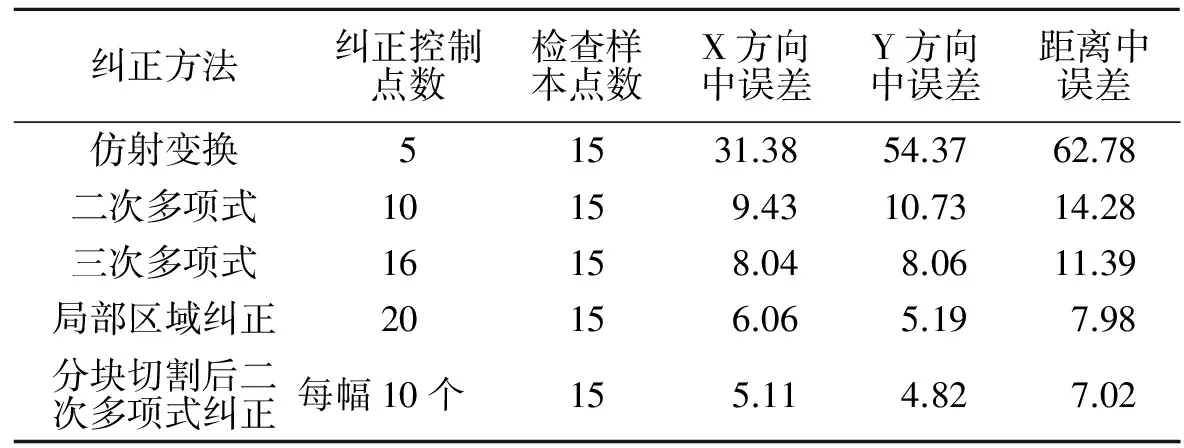
表1 采用分幅切割纠正方法与采用其他纠正方法的精度比较(单位：m)Tab.1 Corrected by framing cutting methods and precision of the method used to correct the other comparison ( units: m)

在每幅经过精确纠正的乡镇基本农田图像上选择15个明显地物点,读取其在1∶10 000地形图上的坐标值(x1,y1),然后分别读取其在使用以上5种纠正方法得到的结果图像上对应点的坐标值(x2,y2)，并使用公式Δx=x1-x2、Δy=y1-y2、Δs=sqr(Δx+Δy)，分别计算地物点的x方向误差、y方向误差和距离误差(见表1).从表中可见，采用分幅切割纠正方法所产生的误差最小.

4 结论

图像的整体纠正方法是把图像的局部几何形变平均分配到整个图像中，因此该方法无法解决图像的非线性局部几何形变[2].由于基本农田图像存在较严重的相对几何形变，因此采用局部区域纠正方法所产生的纠正结果比传统的全局多项式方法要精确些，但其只有在纠正区域的控制点来自同一图幅时才有比较好的纠正结果，而当控制点来自2个或多个不同的图幅时，其纠正结果仍然无法满足要求.因此只有采用分幅切割后再分幅纠正的方法，才能很好的解决基本农田图像的精确纠正问题.

[1] 童小华，周德意.地形(籍)图扫描纠正的精度分析[J].同济大学学报：自然科学版，2003,31(1):77-81.

[2] 颉耀文，岳文泽，徐建华.数字图像纠正和GIS技术在土地详查中的应用[J].测绘通报，2002(10):48-50.

[3] 张文武,尉宇.基于快速Hough变换的图像纠正[J].机械工程与自动化,2010(2):23-24.

[4] 闫利, 郭勤.高精度图像对准关键技术研究[J].红外与激光工程,2007,36(增):231-233.

[5] 张晓东,李德仁, 龚健雅,等.一种基于面特征的遥感影像与GIS数据配准方法[J].遥感学报,2006,10(3)：373-380.

[6] 曾振华,杨利兵.大比例尺地形图数字化精度分析[J].地矿测绘,2004,20(1):30-31.

[7] 凌海滨,吴兵. 一个基于扫描转换的图像格网处理通用算法[J].计算机辅助设计与图形学学报,2001,13(3):259-263.

[8] 刘百胜,蒋岳新.探求航空遥感图像几何纠正的新方法[J].林业资源管理,1988(1):59-64.

[9] Val Noronha.Towards ITS Map Database Interoperability—Database Error and Rectification[J].GeoInformatica,2000,4(2):201-213.

[10] Shi Wenzhong,Ahmed Shaker.Approximate approaches to geometric corrections of high resolution satellite imagery[J].Geo-Spatial Information Science,2004,7(1):24-30.