Lp-新几何体极的几个不等式

朱保成,李 妮

(1.重庆能源职业学院 数理科学系，重庆 400047;2.建始县第一中学,湖北 建始 445300)

1 主要结果

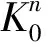
h(K,x)=max{x·y∶y∈K}，x∈Rn，

其中x·y是Rn中通常的内积.

在Rn中，一个紧的星形(包含原点)的径向函数，ρK=ρ(K，·)，定义为:

ρ(K,x)=max(λ≥0∶λx∈K}，x∈Rn{0}

在Rn中，凸体K的极体[1-3],定义为K*={x∶x·y≤1,y∈K}.对于凸体K的极体有如下的性质:

(1)

如果K为Rn中关于原点的星形集，p≥1,如下定义Lp-类质心体TpK∈κn,其范数满足:

(2)

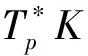
cn,p=ωn+p/ω2ωnωp-1.

(3)

另外极坐标形式的定义为:

(4)

(5)

这里∀u∈Sn-1，且Sp(K,·)是Sn-1上的正的Borel测度，又称K的Lp-表面积测度，并有Radon-Nikodyrn导数:

将这两个概念与Lp混合体积Vp和娇对偶混合体积V-p联立起来，继续研究LP-类质心体TpK和类新几何体T-pK,获得了关于LP-类质心体TpK和类新几何体T-pK极体的几个有趣的不等式如下:

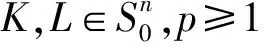
(6)

等号成立当且仅当K=L.

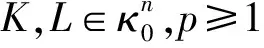
(7)

等号成立当且仅当K=L.

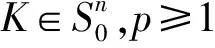
(8)

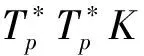
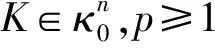
(9)

2 准备工作

2.1 Lp-混合体积

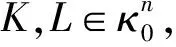
h(K+pε·L,·)=h(K,·)p+εh(L,·)p

这里的“ε·L”中的“·”表示Firey内积.

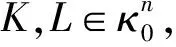
(10)

(11)

Vp(K,K)=V(K).

(12)

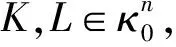
(13)

等号成立当p=1时当且仅当K和L是位似的，当p>1时当且仅当K和L中一个是另一个的膨胀.

2.2 Lp-对偶混合体积

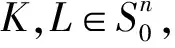
ρ(K+-pε·L,·)-p=h(K,·)-p+εh(L,·)-p

这里的“ε·L”和Firey内积中的“ε·L”是不同的.

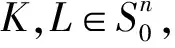
(14)

根据上述定义和体积的极坐标公式，Lutwak在文献[6]中给出了如下的Lp-对偶混合体积V-p(K,L)功的积分表达式：

(15)

V-p(K,K)=V(K).

(16)

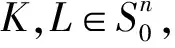
(17)

等号成立当且仅当K和L中一个是另一个的膨胀.

2.3 Jensen不等式

假设p≠0，μ是一个集合X上的有限Borel测度，f是集X上的非负μ-可积函数，则f的p次平均岭f定义为：

和:

关于f的p次平均Mpf,有如下著名的Jensen不等式[8]：如果p≤q且Mpf存在，则:

Mpf≤Mqf,

(18)

等号成立当且仅当f是一个常数或p=q.

3 定理的证明

为了证明定理1，先给出了如下的引理:

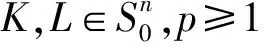
(19)

证明由关系式(1)，有:

由LP-对偶混合体积V-p的定义，可得:

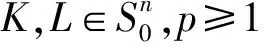
V-p(Q,K)=V-p(Q,L)

3.1 定理1的证明

由引理1(式(19))上式即为:

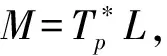
(20)

因此：

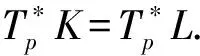
要证明定理2还需要引入以下结果：

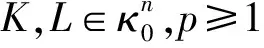
(21)

证明由Lp-混合体积Vp的定义，可得:

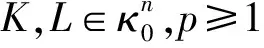
Vp(Q,K)=Vp(Q,L)

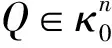
3.2 定理2的证明

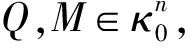
由引理3上式即为:

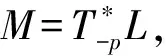
(22)

因此:

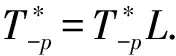
3.3 定理3的证明

所以:

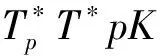
3.4 定理4的证明

所以:

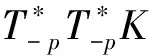
利用定理3和定理4的结果，直接得到：

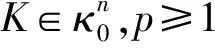
最后利用类质心体TpK的极体容易获得一个关于类质心体TpK的单调性结论：

等号成立当且仅当p=q.

证明当1≤p≤q<∞时，利用定义(2)和Jensen不等式(18)，知道：∀u∈Sn-1，有:

∀u∈Sn-1成立，即有:

等号成立当且仅当p=q.证毕.

[1] Gardner R J.Geometric Tomography[M].Cambridge:Cambridge Univ Press,1995.

[2] Gardner R J.Geometric Tomography(2ed)[M].Cambridge:Cambridge Univ Press,2006.

[3] Schneider R.Convex Bodies:The Brunn-Minkowski theory[M].Cambridge:Cambridge Univ Press,1993.

[4] Firey W J.p-means of convex bodies[J].Math Scand,1962,10:17-24.

[5] Lutwak E.The Brunn-Minkowski-Firey I: mixed volumes and the Minkowski problem[J].J Differential Geom,1993,38:131-150.

[6] Lutwak E.The Brunn-Minkowski-Firey II: Affine and Geominimal Surface Areas[J].Adv Math,1996,118:244-294.

[7] Lutwak E,Yang D,Zhang G. Lp affine isoperimetric inequalities[J].J Differential Geom,2000,56:111-132.

[8] Hardy G H,Littlewood J E,Pólya G.Inequalities[M].Cambridge:Cambridge University Press,1959.