低碳城市发展进程评估模型的研究

杨德志

(辽东学院 师范学院，辽宁 丹东 118001)

“发展低碳经济，建设低碳城市”就是发展低污染、低排放、低能耗的绿色经济，建设跟适合人类居住的家园，其核心是能源技术和减排技术创新、产业结构和制度创新以及人类生存发展观念的根本性转变[1].在全面推进低碳经济发展，建设低碳城市时，构建低碳城市发展的评价指标体系，对低碳城市发展的历程进行评价显得尤为重要.因此，本文先利用层次分析法建立评价体系，得到低碳经济对城市发展的影响，这种方法是一种简单有效的评价方法.

1 低碳城市评价体系的构建

1.1 层次分析模型

基于2009-2020中国低碳城市发展战略目标的考虑，以低碳城市评价指标为目标层，以经济发展系统、低碳技术系统、低碳环境系统以及低碳社会系统准则层，具体方案如下图1所示[2].

1.2 构造各层次的判断矩阵并对其进行一致性检验

层次分析法在使用过程中，关键就是目标值的确定.本文为了力求目标植的科学性和合理性，根据2009-2020中国低碳城市发展战略目标、中国2010年上海世博会环境报告、2000-2009年上海统计年鉴，低碳城市的目标值以及专家咨询的方式确定各个指标的目标植[3-5].

表1 准则层的一致性检验结果

表2 经济发展系统的一致性检验结果

表3 低碳技术系统的一致性检验结果

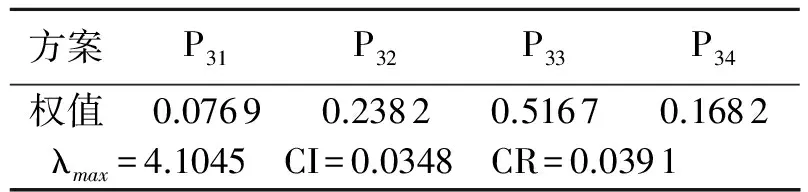
表4 低碳环境系统的一致性检验结果Tab.4 Low-carbon environment system′s the test results of consistency

1.2.1 构造准则层对目标层的判断矩阵及一致性检验

构造经济发展系统、低碳技术系统、低碳环境系统以及低碳社会系统这4个准则指标对城市低碳经济评价指标重要性的判断矩阵如下所示：

运用MATLAB进行一致性检验，结果如表1所示，此判断矩阵的一致性可以接受.

1.2.2 指标层对准则层的判断矩阵及一致性检验

1)经济发展系统的判断矩阵及一致性检验：

运用MATLAB进行一致性检验，结果如下表2，此判断矩阵的一致性可以接受.

2)低碳技术系统的判断矩阵及一致性检验:

运用MATLAB进行一致性检验，结果如表3，此判断矩阵的一致性可以接受.

3)低碳环境系统的判断矩阵及一致性检验：

运用MATLAB进行一致性检验，结果如表4，此判断矩阵的一致性可以接受.

4)低碳社会系统的判断矩阵及一致性检验:

运用MATLAB进行一致性检验，结果如表5，此判断矩阵的一致性可以接受.

表5 低碳社会系统的一致性检验结果Table 5 Low-carbon society system′s the test results of consistency

表6 2000-2009年低碳城市发展进程得分Tab.6 The score of development of Low-carbon city from 2000 to 2009

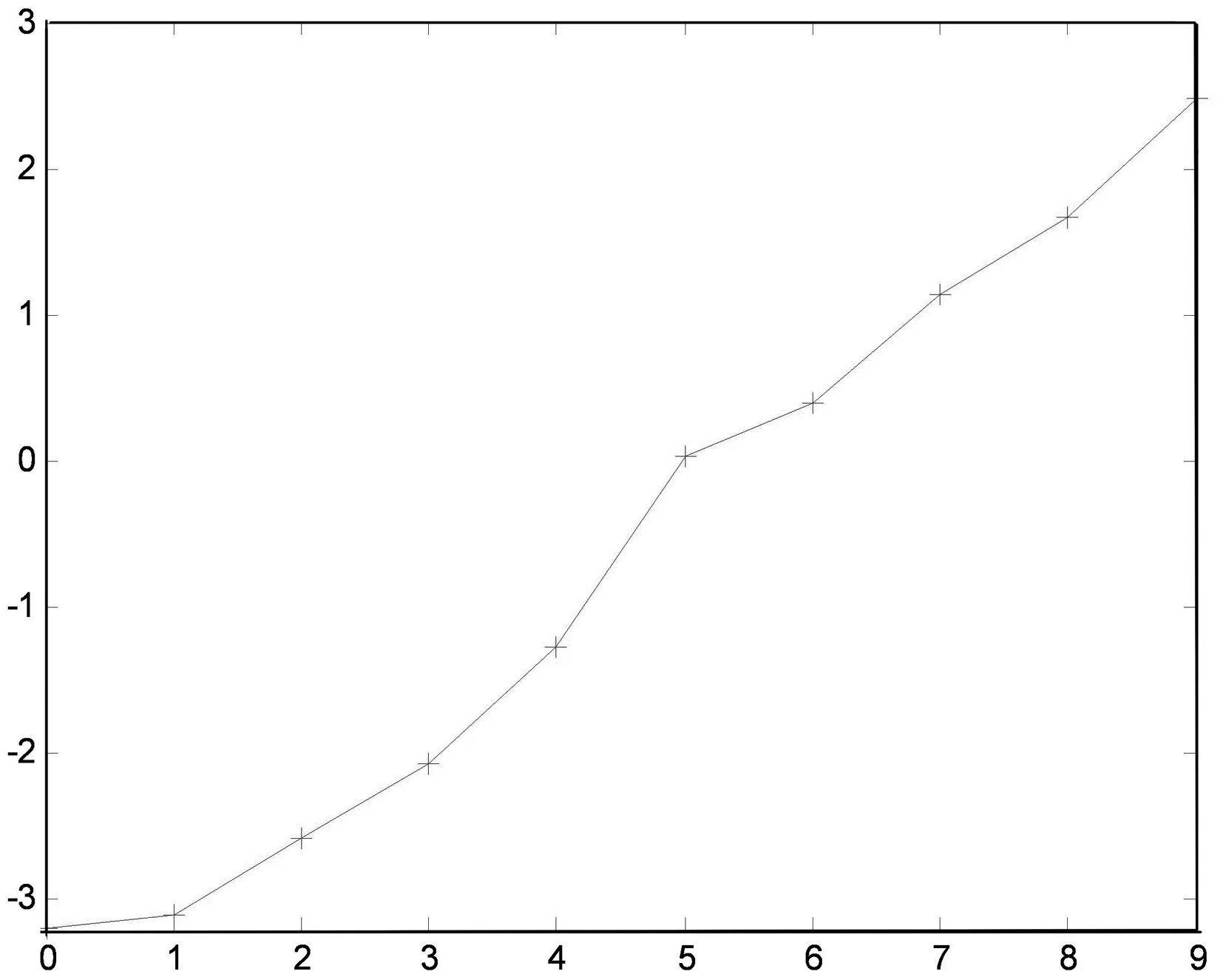
图2 2000-2009年低碳城市发展进程图Fig 2 The figure of development of low-carbon city from 2000 to 2009

1.3 2000-2009年上海市低碳城市发展进程

为了定量分析世博会对上海低碳城市发展进程的影响，本文设定了一个低碳城市指标得分系统，即将方案层21个指标在2000-2009年期间每一年的原始数据先进行标准化处理得到相应数据，再将标准化后的数据乘以各自的权重再乘以对应的目标层的权重，最终的得分即衡量每一年低碳城市发展进程(得分越大，则低碳城市发展进程越快).则具体步骤如下 ：

首先，对方案层21个指标的原始数据进行标准化处理， 本模型采用的数据标准化公式为[6]：

其中i=1,2,…,10；j=1,2,…,21.i的值分别代表2000-2009年，j分别代表方案层21个指标，并运用MATLAB软件，求得标准化后的21个指标值. 然后，根据所设定的公式：每年低碳城市发展进程得分=标准化后的数据×各自的权重×对应的目标层的权重.运用MATLAB软件得出最终的结果如表6所示.

根据表6数据，绘制为使低碳城市发展进程图，如图2所示.

通过图2可以看出，上海2000-2009年低碳城市发展直线上升趋势明显.

2 结论

上海在近年低碳城市建设中，非常注重低碳经济系统的建设，同时也比较重视低碳技术系统、低碳环境系统的建设.低碳社会系统有待提高，其中在机动车保有量变化趋势方面建设需采取紧急措施，居民低碳理念方面需进一步提高.

[1] 李俊峰，马玲娟.低碳经济是规制世界发展格局的新规则[J].世界环境，2008(2)：17-20.

[2] 李晓燕.基于模糊层次分析法的省区低碳经济评价探索[J].华东经济管理，2010，24(2)：24-28.

[3] 中国科学院可持续发展战略研究组.2009中国可持续发展战略报告[M].北京：科学出版社，2009：199-230.

[4] 上海世博会事务协调局上海市环境保护局.中国2010年上海世博会环境报告[R].上海：上海市环境保护局，2009:8-46.

[5] 上海统计局.上海统计年鉴[M].北京：中国统计出版社，2000-2009.

[6] 何晓群.多元统计分析[M].2版.北京：中国人民大学出版社，2010:152-174.