二阶变系数线性微分方程及其衍生方程

李 高，常秀芳

（山西大同大学煤炭工程学院，山西 大同037003）

二阶变系数线性微分方程及其衍生方程

李 高，常秀芳

（山西大同大学煤炭工程学院，山西 大同037003）

目的 探究二阶变系数线性微分方程的求解．方法 从构造二阶变系数线性微分方程解的形式出发，给出正负各级衍生方程的概念．结果 得到二阶线性微分方程衍生方程的存在性，各级衍生方程的递推公式，导出二阶变系数线性微分方程与衍生方程解的关系．结论 得到二阶变系数线性微分方程求解方法的重要结论．

二阶变系数齐次线性微分方程；初始方程；衍生方程；衍生方程的存在性；递推公式

现行 《高等数学》中的方程，只是对常系数微分方程的情况做了详细的讨论，即使 《常微分方程》也未对二阶变系数微分方程的解作进一步的阐述．

对二阶变系数线性微分方程由 《常微分方程》教材知，只要能求出二阶变系数齐次线性微分方程的一个特解，则二阶变系数线性齐次或非齐次微分方程的解即可求得［1］．尽管目前国内外专家学者进行了大量的研究也给出了特殊类型的二阶变系数线性微分方程的求解法［2－5］，以及采用构造降阶法求二阶变系数线性微分方程的通解［6］．然而到目前为止，如何求出其中的某一特解是无法可循的．本文从构造解的形式给出衍生方程，诣在解决二阶变系数线性微分方程求解的问题，并得出成规求解的方法．

1 衍生方程

假设二阶变系数线性微分方程

的解的形式为

对 （2）求导

将 （2）、（3）、（4）式代入 （1）式，并整理得

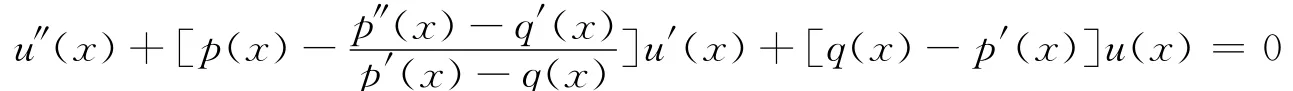
则把方程 （5）就称为方程 （1）的正一级衍生二阶变系数线性微分方程，简称一级衍生方程，而方程（1）称为初始方程或零级衍生方程．

而由方程 （5）得到的一级衍生方程

可规定为方程 （1）的正二级衍生二阶变系数线性微分方程，简称二级衍生方程．依此类推，由方程 （1）的n－1级衍生方程可推得方程 （1）的n级衍生方程

其中

综上所述，可以把方程 （1）定义为方程 （5）的负一级衍生二阶变系数线性微分方程，简称负一级衍生方程，而方程 （5）称为初始方程或零级衍生方程；方程 （1）称为方程 （6）的负二级衍生二阶变系数线性微分方程，简称负二级衍生方程，而方程 （6）称为初始方程或零级衍生方程；依此类推，方程 （1）称为方程 （7）的负n级衍生方程，而方程 （7）称为初始方程或零级衍生方程．注意的是衍生方程的级数又是相对的，初始方程或零级衍生方程也是相对的，而正负二级或以上的衍生方程通称为高级衍生方程．

若记p0（x）＝p（x），q0（x）＝q（x），则 （8）式就称为二阶变系数非齐次线性微分方程的正级衍生方程系数的通项公式．

又由 （8）式可得

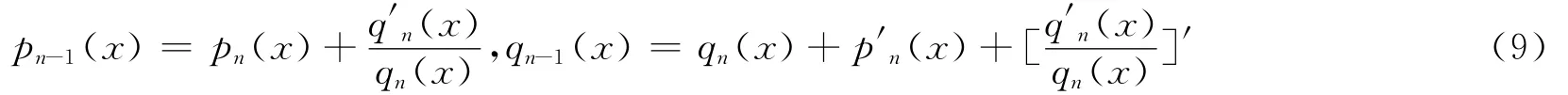
则 （9）式就称为二阶变系数非齐次线性微分方程的负级衍生方程系数的通项公式．

2 衍生方程的存在性

由衍生方程系数通项公式 （8）或 （9）知，p（x）、q（x）均为常数时，方程就没有衍生方程，即常系数线性微分方程无衍生方程，这也就是说常系数线性微分方程的解为什么有成规的欧拉法［7］，而变系数线性微分方程为什么没有成规求解法的原因所在．

3 方程与衍生方程的解

3．1 负一级衍生方程的解

由衍生方程概念知，初始方程的解正好是负一级衍生方程所设解的形式 （2）中的函数u（x），因此，若初始方程的解是已知的，设为u（x），按 （2）式即可求得负一级衍生方程的解．

3．2 正一级衍生方程的解

若初始方程的解是已知的，设为y，则由 （3）式可得正一级衍生方程的解u（x）

综上所述，只要初始方程的解是已知的，即可求得各级衍生方程的解或通解，又由于衍生方程的级数是相对的，所以只要在各级衍生方程中能够知道其中某级衍生方程的解或通解，就可以求得二阶变系数线性微分方程的解或其通解．但在多数情况下，随着衍生级数的增大，得到的衍生方程就会越来越复杂，其通解也会随之愈来愈繁琐．为此，通过衍生方程求二阶变系数线性微分方程的解时，观察二阶变系数线性微分方程的特征，依据问题应灵活使用．

4 举例

例 已知初始方程

的通解

求其正、负一级衍生方程及其通解．

解 根据p0（x）＝tanx，q0（x）＝－cos2x

当n＝0时，由 （9）式得

则所求方程的负一级衍生方程为

而由初始方程知其两个线性无关的特解为

由 （2）可得负一级衍生方程两个线性无关的特解为

故所求方程的负一级衍生方程的通解为

当n＝1时，由 （8）式得

则所求方程的正一级衍生方程为

又由 （10）可得正一级衍生方程两个线性无关的特解为

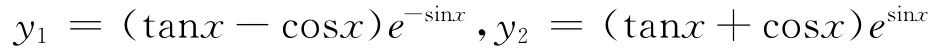
故所求方程的正一级衍生方程的通解为

［1］ 王高雄．常微分方程 ［M］．北京：高等教育出版社，1985：1－46

［2］ 常秀芳，李高．伯努利方程的几种新解法 ［J］．雁北师范学院学报，2007，23（02）：89－91

［3］ 李录苹，王通．关于几类二阶微分方程的解法 ［J］．雁北师范学院学报，2006，22（02）：71－72

［4］ 李高，常秀芳．不定方程x2＋y2＋z2＝2（xy＋yz＋xz）的解及其性质 ［J］．山西大同大学学报，2011，27（03）：6－10

［5］ 常秀芳，李高．股票涨跌中数学模型的研究 ［J］．河北北方学院学报：自然科学版，2008，24（06）：63－66

［6］ 李高，常秀芳．关于二阶变系数线性微分方程求解法的研究［J］．河北北方学院学报：自然科学版，2010，26（06）：12－19

［7］ 同济大学应用数学系．高等数学 ［M］．北京：高等教育出版社，2003：259－317

Second－order Variation Coefficient Linear Differential Equation and Its Derivative Equation

LI Gao，CHANG Xiu－fang
（School of Coal Engineering，Shanxi Datong University，Datong 037003，Shanxi，China）

Objective To explore the solution to second－order variation coefficient linear differential equations．Methods By constructing the models of the solution to this kind of equation，the concept of all levels of derivative equations is obtained．Results The existence of the derivative equations，and the recurrence formula of those equations are obtained，and the relations between the primitive equation and the derivate equations are deduced．Conclusion Important conclusions of the solution to this kind of equations are obtained．

second－order variation coefficient linear differential equation；primitive equation；derivative equation；existence of derivative equations；recurrence formula

O 175．1

A

1673－1492 （2011）05－0013－03

来稿日期：2011 07 13

李高（1965－），男，山西天镇人，山西大同大学煤炭工程学院副教授．

常秀芳 （1965－），女，山西应县人，山西大同大学煤炭工程学院副教授．

刘守义 英文编辑：刘彦哲］