有r个悬挂点仙人掌图的零阶广义Randic指数的界

吕宁宁，马艳丽

（安徽新华学院公共课教学部，安徽 合肥230088）

有r个悬挂点仙人掌图的零阶广义Randic指数的界

吕宁宁，马艳丽

（安徽新华学院公共课教学部，安徽 合肥230088）

设G为一简单连通图，则G的零阶广义Randic指数定义为R0α（G）＝∑ν∈V（G）dα（ν），其中d（v）为顶点ν的度数，α为非0和1的实数．图G称之为仙人掌图，如果G的每一块要么是一条边，要么是一个圈．本文研究有r个悬挂点仙人掌图的零阶广义 Randic指数的界．L（n，r）、G（n，r）、H（n，r）、M（n，r）、N（n，r）分别表示一类图．当α＜0时，R0αG）取得极大值当且仅当G∈M（n，r），R0α取得极小值当且仅当G∈N（n，r）；当0＜α＜1时，R0α取得极大值当且仅当G∈N（n，r），R0α取得极小值当且仅当G∈M（n，r）；当α＞1时，R0α取得极大值当且仅当G∈G（n，r），R0α取得极小值当且仅当G∈H（n，r）．

仙人掌图；零阶广义Randic指数；界

1 引 言

给定一个简单连通图G＝（V（G），E（G）），其中V（G），E（G）分别表示图G的顶点集合和边集合．图G的Randic指数定义为：，其中d（u）表示顶点u的度数［1］．

1998年Bollobas与Erdos［2］将 Randic指数进行了推广，得到广义 Randic指数，即Rα（G）＝其中α为任意实数．零阶 Randic指数是由 Kier与 Hall［3］提出，定义为R0（G）＝阶广义Randic指数［4］定义为：其中α为任意实数．零阶广义Randic指数的相关研究结果已有许多［5－7］．

图G称之为仙人掌图，如果G的每一块要么是一条边，要么是一个圈．含两个圈的仙人掌图称为双圈仙人掌图．M．Lu［8］给出了给定圈数的Randic指数下界，A．Lin［9］给出了有r个悬挂点仙人掌图的Randic指数下界，其它相关研究结果见文献 ［10－15］．本文探讨有r个悬挂点仙人掌图的零阶广义Randic指数的界．

首先介绍一些定义．Δ（G），δ（G）分别表示图的顶点最大度和最小度；ni表示度数为i的顶点个数；Cn、Pn分别表示有n个顶点的圈和路；度数为1的顶点称为悬挂点．L（n，r）表示有r个悬挂点的n阶连通仙人掌图的集合．G（n，r）表示：当n－r－1为偶数时，在星图Sn上添加 （n－r－1）／2条独立边，当（n－r－1）为奇数时，在星图Sn－1上添加 （n－r－1）／2条独立边，并在其中一条独立边或悬挂边上插入一个2度顶点．H（n，r）表示：一条长为n－r＋1的路Pn－r＋1，在其中k0个2度点上添加k＋1条悬挂边，在其余的n－r－k0个2度点上添加k条悬挂边，其中r－2＝（n－r）k＋k0（k≥0，k0≥0，k0＜n－r）．M（n，r）表示在星图Sr＋1的边上插入n－r－1个2度点．N（n，r）表示：当n－r－1为偶数时，（n－r－1）／2个C3相连接，并且每两个圈至多有一个公共点，则这样得到的图有度点，若r≤n－r＋3，令在其中k个2度点上添0加k＋1条悬挂边，在其余的2度点上添加k条悬挂边，若r＞n－r＋3，则在每个2度点上添加两条悬挂边，令r－（n－r＋3）＝2r－n－3＝（n－r）k＋k0，然后在其中的k0个4度点上添加k＋1条悬挂边，在其余的n－r－k0个4度点上添加k条悬挂边；当n－r－1为奇数时，（n－r－4）／2个C3与一个C4相连接，并且每两个圈至多有一个公共点，则这样得到的图有4度点，有个2度点，当r≤n－r＋4时，令k0个2度点上添加k＋1条悬挂边，在其余的个2度点上添加k条悬挂边，若r＞n－r＋4，则在每个2度点上添加两条悬挂边，令r－（n－r＋4）＝2r－n－4＝（n－r）k＋k0，然后在其中的k0个4度点上添加k＋1条悬挂边，在其余的n－r－k0个4度点上添加k条悬挂边．

2 引 理

为了以后的定理证明，首先给出几个引理．

引理1［10］若a，b是正实数，且满足a－2≥b≥1，则有

（1）当α∈ （－∞，0）∪ （1，＋∞）时，aα＋bα＞ （a－1）α＋（b＋1）α

（2）当α∈ （0，1）时，aα＋bα＜ （a－1）α＋（b＋1）α

引理2［10］若a，b是正实数，且满足a≥b≥2，则有

（1）当α∈ （－∞，0）∪ （1，＋∞）时，aα＋bα＜ （a＋1）α＋（b＋1）α

（2）当α∈ （0，1）时，aα＋bα＞ （a＋1）α＋（b－1）α

引理3 当x＞0时，对于y＝（x＋1）α－xα，有

（1）当α＞0时，y＞0

（2）当α＜0时，y＜0

3 主要结论

当r＝n－1时，此时图为星图Sn，所以只考虑r≤n－2．

定理1 设图G∈L（n，r），即G是有r个悬挂点的n阶仙人掌图，若r＝n－2，则

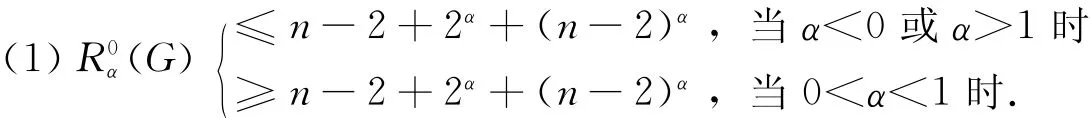
等号成立当且仅当G为：在星图Sn－1的一条边上插入一个2度点．

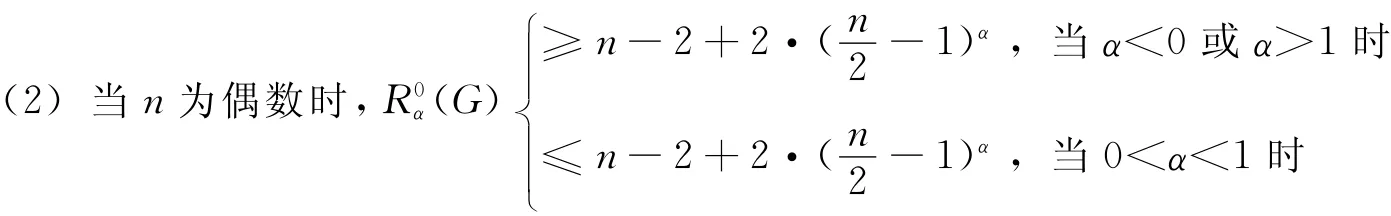
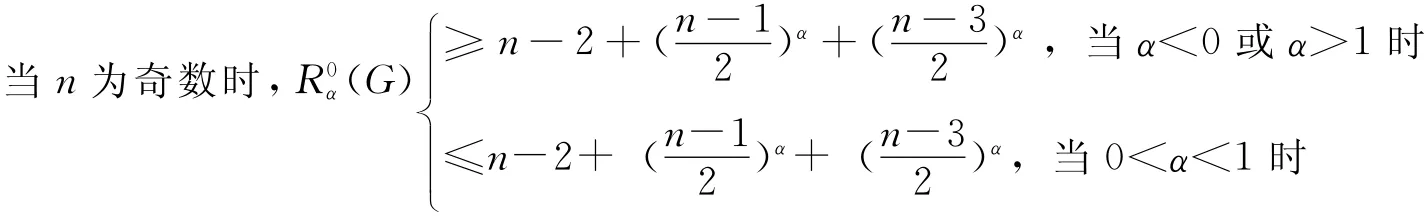
证明 因为G有n－2个悬挂点，那么G正好有2个顶点度数≥2．设这两个顶点为x，y，则可知G为树．因为G连通，悬挂点个数为n－2，我们可以得到n≥4，x与y相邻，且对于任意一个悬挂点z要么与x相邻，要么与y相邻．设a，b分别为顶点x，y的度数，则a＋b＝n，不妨设a≥b．

先看 （1）的证明：

1）若b＝2，则G就是由Sn－1对其中一边插入一个2度点所得到的图．

2）若b≥3，则顶点y至少有2个悬挂点，设其中一个悬挂点为z，则可以构造一个新的图G′＝G－yz＋xz，显然G′∈L（n，r），则由引理2可知

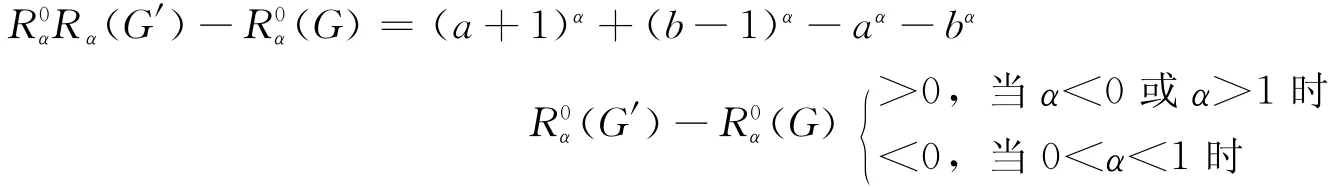
由1）、2）可知，b＝2，即此时的极值图G为：在星图Sn－1的一条边上插入一个2度点．

再看 （2）的证明：只证明n为偶数的情形，n为奇数时类似可证．

因为a＋b＝n，则当n为偶数时，

2

2）若a＞b，则有a－2≥b≥2，此时我们假设x的一个悬挂点为z，则我们可以构造一个新的图G′＝G－xz＋yz，显然G′∈L（n，r），则由引理1可知

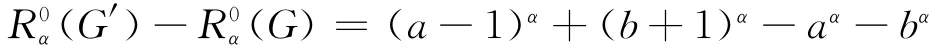
定理2 设图G∈L（n，r），即G是有r个悬挂点的n阶仙人掌图，若r≤n－3，则

证明 （1）1）设G为α＜0时零阶广义Randic指数取得最大的图，则有如下断言：

断言1 G不含圈．

假设G含圈Cm∶x1x2…xmx1，则若去掉其中任意一边，不妨设去掉边x1xm后得到图G′＝G－x1xm，显然G′∈L（n，r）．则由引理3可知

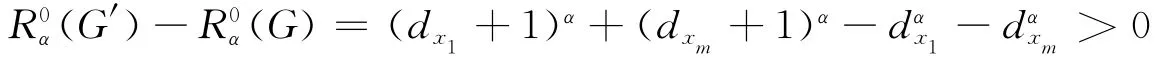
所以可知G不含圈．

断言2 G的顶点度数要么为1，要么为2，要么为Δ（G）．

假设还有其他度数，不妨设G中顶点x有最大度Δ（G），顶点y度数满足条件Δ（G）≥y≥3，则可知顶点y至少有一邻点z满足任意一条zx路经过顶点y，构造图G′＝G－yz＋xz，显然G′∈L（n，r），则由引理2可知

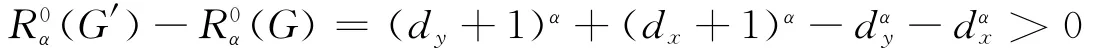
所以可知G的顶点度数要么为1，要么为2，要么为Δ（G）．

由断言1和断言2可知，当α＜0时，R0α取得极大值当且仅当G∈M（n，r）．

2）设G为α＜0时零阶广义Randic指数取得最小的图，则有如下断言：

断言1 G含圈的个数越多越好．

假设G不含圈，则可以加一边xy后得到一个新的图G′＝G＋xy，显然G′∈L（n，r）．则由引理3可知

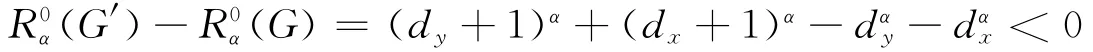
所以G含圈，而且含圈的个数越多越好．

断言2 G中任意三圈不交于同一顶点．

假设有三个圈C1、C2、C3交于同一顶点x，不妨设y为圈C2上且异于x的顶点，设顶点w、z与顶点x关联且为圈C1上的点．构造新图G′＝G－wx－zx＋wy＋zy，显然G′∈L（n，r）．此时dx－4≥dy≥2，则由引理1可知

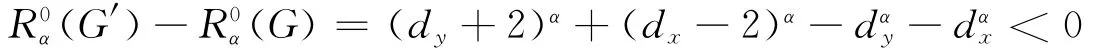
所以G中任意三圈不交于同一顶点．

断言3 G中顶点度数要么为1，要么为2，要么为3，要么为4（此时度数为4的顶点无悬挂边）；或者要么为1，要么为Δ（G），要么为Δ（G）－1．

这也就是说尽量将悬挂边平均分到顶点上，且使得顶点度数尽量接近．

假如不按照这种方法分配悬挂边，则会得到一图G，G中有两顶点x、y满足dx－2≥dy≥2且x至少有一悬挂边xz．可以得到一新图G′＝G－zx＋zy，显然G′∈L（n，r）．则由引理1可知

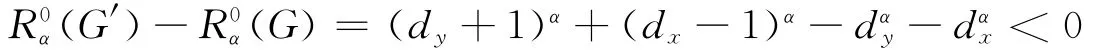
（2）1）设G为0＜α＜1时零阶广义Randic指数取得最大的图，则有如下断言：

断言1 G含圈的个数越多越好．

假设G不含圈，则可以加一边xy后得到一个新的图G′＝G＋xy，显然G′∈L（n，r）．则由引理3可知

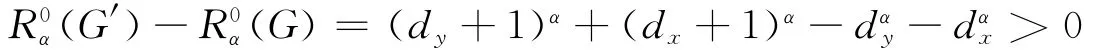
所以G含圈，而且含圈的个数越多越好．

断言2 G中任意三圈不交于同一顶点．

假设有三个圈C1、C2、C3交于同一顶点x，不妨设y为圈C2上且异于x的顶点，设顶点w、z与顶点x关联且为圈C1上的点．我们构造新图G′＝G－wx－zx＋wy＋zy，显然G′∈L（n，r）．此时dx－4≥dy≥2，则由引理1可知

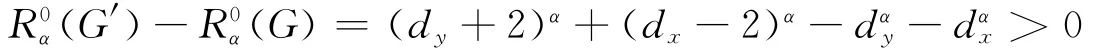
所以G中任意三圈不交于同一顶点．

断言3 G中顶点度数要么为1，要么为2，要么为3，要么为4（此时度数为4的顶点无悬挂边）；或者要么为1，要么为Δ（G），要么为Δ（G）－1．

这也就是说尽量将悬挂边平均分到顶点上，且使得顶点度数尽量接近．

假如不按照这种方法分配悬挂边，则会得到一图G，G中有两顶点x、y满足dx－2≥dy≥2且x至少有一悬挂边xz．可以得到一新图G′＝G－zx＋zy，显然G′∈L（n，r）．则由引理1可知

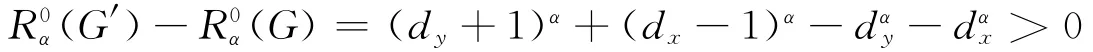
由断言1、断言2和断言3可知，当α＜0时，R0α取得极小值当且仅当G∈N（n，r）．

2）设G为0＜α＜1时零阶广义Randic指数取得最小的图，则有如下断言：

断言1 G不含圈．

假设G含圈Cm∶x1x2…xmx1，则若去掉其中任意一边，不妨设去掉边x1xm后得到图G′＝G－x1xm，显然G′∈L（n，r）．

则由引理3可知

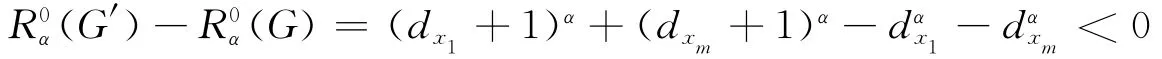
所以可知G不含圈．

断言2 G的顶点度数要么为1，要么为2，要么为Δ（G）．

假设还有其他度数，不妨设G中顶点有x最大度Δ（G），顶点y度数满足条件Δ（G）≥y≥3，则可知顶点y至少有一邻点z满足任意一条zx－路经过顶点y，构造图G′＝G－yz＋xz，显然G′∈L（n，r），则由引理2可知

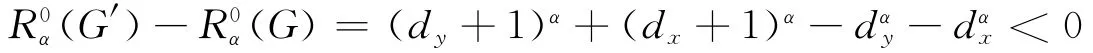
所以可知G的顶点度数要么为1，要么为2，要么为Δ（G）．

由断言1和断言2可知，当0＜α＜1时，R0α取得极大值当且仅当G∈M（n，r）．

（3）1）设G为α＞1时零阶广义Randic指数取得最大的图，则有如下断言：

断言1 G含圈的个数越多越好．

假设G不含圈，则可以加一边xy后得到一个新的图G′＝G＋xy，显然G′∈L（n，r）．则由引理3可知

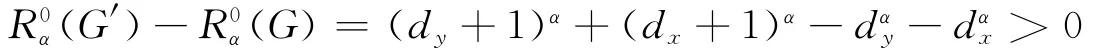
所以G含圈，而且含圈的个数越多越好．

断言2 所有圈交于同一顶点x．

假设存在一圈C，x∉V（C），则必存在路P∶x…y，使得V（P）∩V（C）＝｛y｝．设顶点w、z与顶点y关联且为圈C上的点．构造新图G′＝G＝wy－zy＋wx＋zx，显然G′∈L（n，r）．则由引理2可知

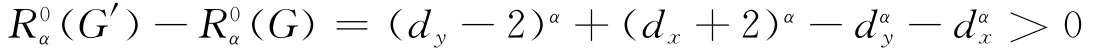
所以G中所有圈交于同一顶点．

断言3 度数为1的顶点必与最大度顶点关联．

假设x，y∈V（G），d（y）＝1，d（x）＝Δ（G）．x与y不相邻，则存在路P∶x…zy．构造新图G′＝G－zy＋xy，显然G′∈L（n，r），则由引理2可知

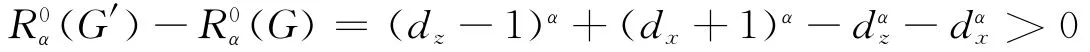
所以可知G的度数为1的顶点必与最大度顶点关联．

由断言1、断言2和断言3可知，当α＞1时，R0α取得极大值当且仅当G∈G（n，r）．

2）设G为α＞1时零阶广义Randic指数取得最小的图，则有如下断言：

断言1 G不含圈．

假设G含圈Gm∶x1x2…xmx1，则若去掉其中任意一边，不妨设去掉边x1xm后得到图G′＝G－x1xm，显然G′∈L（n，r）．则由引理3可知

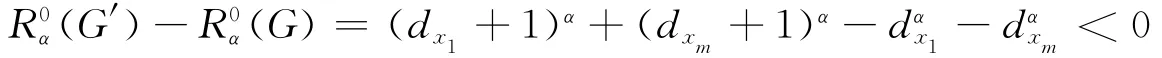
所以可知G不含圈．

断言2 G中除1度点外，顶点度数要么为Δ（G），要么为Δ（G）－1．

假设图G中有两顶点x，y度数满足dx－2≥dy≥2，则可知顶点x至少有一邻点z满足任意一条zy－路经过顶点x，我们构造图G′＝G－xz－yz，显然G′∈L（n，r），则由引理1可知

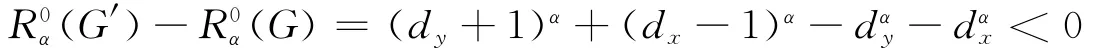
由断言1和断言2可知，当α＞1时，R0α取得极小值当且仅当G∈H（n，r）．

［1］ Randic M．On the characterization of molecular branching ［J］．J Am Chem Soc，1975 （97）：6609－6615

［2］ Bollobas B，Erdos P．Graphs of extremal weights ［J］．Ars Combin，1998 （50）：225－233

［3］ Kier LB，Hall LH．Molecular connectivity in structure－analysis ［M］．Wiley，Chichester Research Studies Press，1986

［4］ Pavlovic LJ．Maximal value of the zeroth－order Randic index ［J］．Discrete Appl Math，2003 （127）：615－626

［5］ Hua H，Deng H．On unicycle graphs with maximum and minimum zeroth－order general Randic index ［J］．J Math Chem，2007 （41）：173－181

［6］ Li X，Zhao H．Trees with the first three smallest and largest generalized topological indices［J］．Match Commun Math Chem，2004 （50）：57－62

［7］ Wang H，Deng H．Unicycle graphs with maximum generalized topological indices［J］．J Math Chem，2007（42）：119－124

［8］ Lu M，Zhang L，Tian F．On the Randic index of cacti［J］．Match Commun Math Chem，2006 （56）：551－556

［9］ Lin A，Luo R．A sharp lower bound of the Randic index of cacti with r pendants［J］．Discrete Appl Math Lett，2008（156）：1725－1735

［10］ Lin A，Luo R．On sharp bounds of the zero－order Randic index of certain unicyclic graphs ［J］．Appl Math Lett，2009（22）：585－589

［11］ Bondy JA，Murty USR．Graph Theory［M］．Berlin：Springer，2008

［12］ Randic M．On structural ordering and branching of acyclic saturated hydrocarbons ［J］．J Math Chem，1998 （24）：345－358

［13］ 孙志荣，蒋珍珍．具有极小Hosoya指数的共轭树 ［J］．甘肃联合大学学报，2010．23（01）：17－20

［14］ 刘家保，吕宁宁，潘向峰．一类单圈图的优美性和平衡性 ［J］．合肥学院学报，2008，18（02）：18－22

［15］ 吕宁宁，王春生．双圈仙人掌图的零阶广义Randic指数的界 ［J］．河北北方学院学报：自然科学版，2010，26（03）：10－12

On Bounds of Zero－order General Randic Index of Cacti with r Pendents

LV Ning－ning，MA Yan－li
（Department of Basic Coureses，Xinhua University，Hefei 230088，Anhui，China）

The zero－order general Randic index of a simple connected graph Gis defined as R0α（G）＝∑ν∈V（G）dα（ν），where d（ν）denotes the degree ofν，αis a given real number other than 0and 1．A graph G is called a cactus if each block of Gis either an edge or a cycle．In this paper，we present the sharp bounds of the zero－order general Randic index of cacti with r pendents．L（n，r），G（n，r），H（n，r），M（n，r）andN（n，r）denote some class of cacti respectvely．Whenα＜0，the maximal graph is in M（n，r）and the minimal graph is in N（n，r）；when 0＜α＜1，the maximal graph is in N（n，r）and the minimal graph is in M（n，r）；whenα＞1，the maximal graph is in G（n，r）and the minimal graph is in H（n，r）．

Cactus；Zero－order general Randic index；bound

O 157．5

A

1673－1492 （2011）05－0001－05

来稿日期：2011 06 14

国家自然科学基金项目 （10901001）；安徽新华学院资助科研项目（2011zr006）；安徽新华学院资助科研项目（2011zr007）

吕宁宁（1985－），女，安徽界首市人，安徽新华学院教师，硕士．

刘守义 英文编辑：刘彦哲］