基于自适应理论的谐波检测
张俊敏
(中南民族大学 计算机科学学院,武汉 430074)
1920~1930年间,德国学者提出了静态整流器产生的波形畸变问题,从此谐波问题引起了人们的关注[1,2].电网中的谐波主要是由各种大容量电力和用电变流设备以及其它非线性负载产生的,其中主要的谐波源是各种电力电子装置,包括各种整流装置、交流调压装置、变流装置、电弧炉、办公及家用电器、照明设施等[3-5].传统的谐波抑制方法有两大类,一类是对产生谐波的谐波源装置本身进行改造的方法[6-8],另一类是设置谐波滤波装置的方法.在实际应用中传统谐波抑制方法存在较多问题,目前谐波抑制的一个重要趋势是采用有源滤波器(APF,Active Power Filter)[9-13]检测出谐波电流,对电网中的谐波进行补偿.因此能否准确实时地检测出谐波电流是APF工作的关键.大量文献提出了不同的谐波检测方法,本文在目前常用的自适应类检测方法中挑选了4种比较有代表性的方法进行了分析,以理论推导和仿真来说明这些方法的优缺点,给出各种不同方法的动态过程、时间滞后、计算量以及稳态精度等特性,再比较各类方法之间的相互关系,指出各类方法存在的问题.
1 自适应检测方法
非自适应类方法都存在着难以克服的问题:检测系统是开环的、固定频率的,对元件参数变化和电网频率变化比较敏感,检测精度不高,特别是没有自适应能力,在系统变化时不能较好地跟踪检测[14].对于自适应类的谐波检测方法,最重要的是权值的迭代方式,权值与正弦信号相乘,就是基波信号,谐波减去基波信号就是谐波信号.下面简单介绍4种自适应检测方法中权值的迭代关系.
1.1 基于RLS的谐波检测方法
文献[15]提出了一种基于RLS(递推最小二乘法)的谐波检测方法,递推关系为:
ω(n)=ω(n-1)+K(n)e(n).
(1)
其中:
(2)
e(n)=d(n)-ωH(n-1)x(n).
(3)
P(n)=λ-1P(n-1)-λ-1K(n)xH(n)P(n-1).
(4)
P(n)为自相关矩阵的逆矩阵;λ为遗忘因子;e(n)为误差函数;d(n)为期望信号.
通过对ω(n)和P(n)赋初值,依次执行(2)式、(3)式、(1)式、(4)式,即可完成RLS算法的迭代过程.
1.2 基于变步长的谐波检测方法
一般变步长LMS算法的准则为:当权系数远离最佳权值时,步长比较大,以加快动态响应速度和对时变系统的跟踪速度;当权系数接近最佳权值时,步长比较小,以获得较小的稳态误差.文献[15]~[18]提出的方法比较具有代表性.但将这些文献介绍的变步长算法用于谐波检测时,发现它们对谐波检测性能的改善并不明显.
文献[19]提出了一种变步长自适应谐波检测方法,利用误差信号的时间均值来控制步长更新,以便能够有效地调整步长,保证较快地动态响应速度,并且在更新步长的时候,大大降低了不相关噪声信号的干扰.步长递推公式为:
p(n)=βp(n-1)+(1-β)e(n).
(5)
μ(n+1)=αμ(n)+γp(n).
(6)
式中p(n)称为误差信号e(n)的时间均值估计,0<β<1称为遗忘因子,用来调整时间窗的宽度,以控制过去信号对现在状态的影响;1-β为时间均值估计权系数;参数0<α<1主要控制权值的收敛速度;γ对收敛速度和稳态误差均有较大的影响,为了保证均方误差收敛,同时又要求有较小的失调,通常γ的值选得比较小.该方法的其余公式同LMS法.
1.3 基于自适应干扰对消原理的谐波检测方法
虽然大量文献介绍了各种不同的自适应检测方法,但以文[20]提出的基于自适应干扰对消原理的自适应谐波电流检测法最具代表性,原理如图1所示.
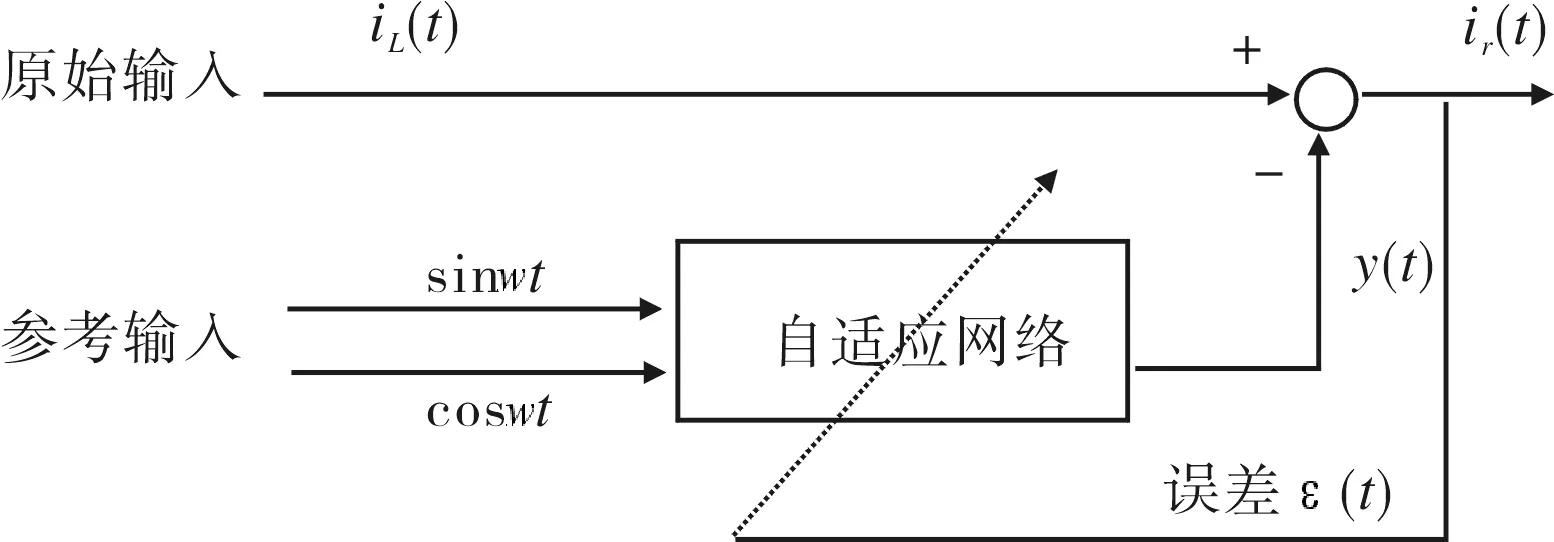
图1 自适应检测原理
[21],[22]中的结果,可以得到自适应检测法的传递函数为:
(7)
其中ω为基波频率,μ为步长.从 (7)式可知,图1所示的系统等效于一个二阶陷波器,其带宽为2μ.与传统的陷波器相比较,图1所示的系统的中心频率唯一取决于参考输入的频率ω,这样的系统对元件参数的依赖性就不大.这是自适应谐波电流检测法最突出的优点.从 (7)式可知,对于某个特定的参考频率ω,系统特性完全取决于步长μ.
1.4 基于模拟化自适应原理的谐波检测方法
文[23]通过分析非线性负载电流的组成特点,提出了一种基于神经元的自适应谐波电流检测方法.算法的仿真说明它与目前采用的几种谐波电流检测方法[24,25]相比,检测速度快、跟踪效果好,而且有较强的自适应能力.
将离散系统模拟化的基本原理是用时间轴上每相邻的2个数据相减后除以信号的采样周期,如果采样周期T取得足够小,就能把离散变量看成连续变量,离散数据的下标k就可以用连续时间变量t来代替.这样得到模拟域中的权值调节函数为:
(8)
其中η为模拟域中的学习率,e(t)为误差函数,xj(t)为自适应的输入.
对于前面提出的基于自适应干扰对消原理的自适应谐波电流检测法模拟后的框图如图2所示.

图2 模拟自适应检测原理
参考文献[6]中的结果,可以得到自适应检测法的传递函数为:
(9)
其中K为图2中积分器的增益.从(9)式可知,图2所示的系统等效于一个二阶陷波器,其带宽为K.和传统的陷波器相比较,图2所示的系统的中心频率唯一取决于参考输入的频率ω,这样的系统对元件参数的依赖性就不大.该检测法在文[20]得到了应用.文献[20,26]通过理论和仿真试验对此检测方法的综合性能做了全面深入细致的分析.在频域和时域里对该检测方法的检测精度和动态响应特性做了详细的分析比较,对于该检测方法在增益大小的选择上有指导性意义.
传统定步长自适应检测方法存在收敛速度和稳态误差之间的矛盾,变步长检测方法的步长更新标准直接或间接来自受噪声污染的瞬时误差,再考虑到APF自身的特殊性:信号信噪比较低,导致实验效果比较差.基于自适应对消原理的谐波电流检测方法是一种经典的检测方法,它的检测性能不依赖于外界环境的变化,并且可以通过调节步长达到需要的检测精度和动态响应,也存在收敛速度和稳态失调之间的矛盾.用连续工作的模拟(硬件)电路来实现自适应算法,结构简单,响应速度快,但直接模拟化的检测系统是存在误差的.因此在基于自适应的谐波检测方法中主要存在2个问题:(1)数字检测方法中定步长方法的改进是否能够同时兼顾良好的收敛速度和稳态误差这2个方面的要求;(2)模拟电路检测方法中需要消除稳定后的权值误差.
2 谐波检测基本方法的比较
2.1 动态过程的比较
对于一个谐波检测系统来说,动态跟随所需要的时间越短表明该系统具有良好的快速性.自适应检测方法中的RLS方法的跟随性能为1个周期,如图3所示;变步长方法的动态跟随性能为2个周期,如图4所示;而基于干扰对消原理的检测方法动态响应时间大概介于3~4个周期,如图5所示;模拟电路方法的动态响应时间大概为2个周期,如图6所示.
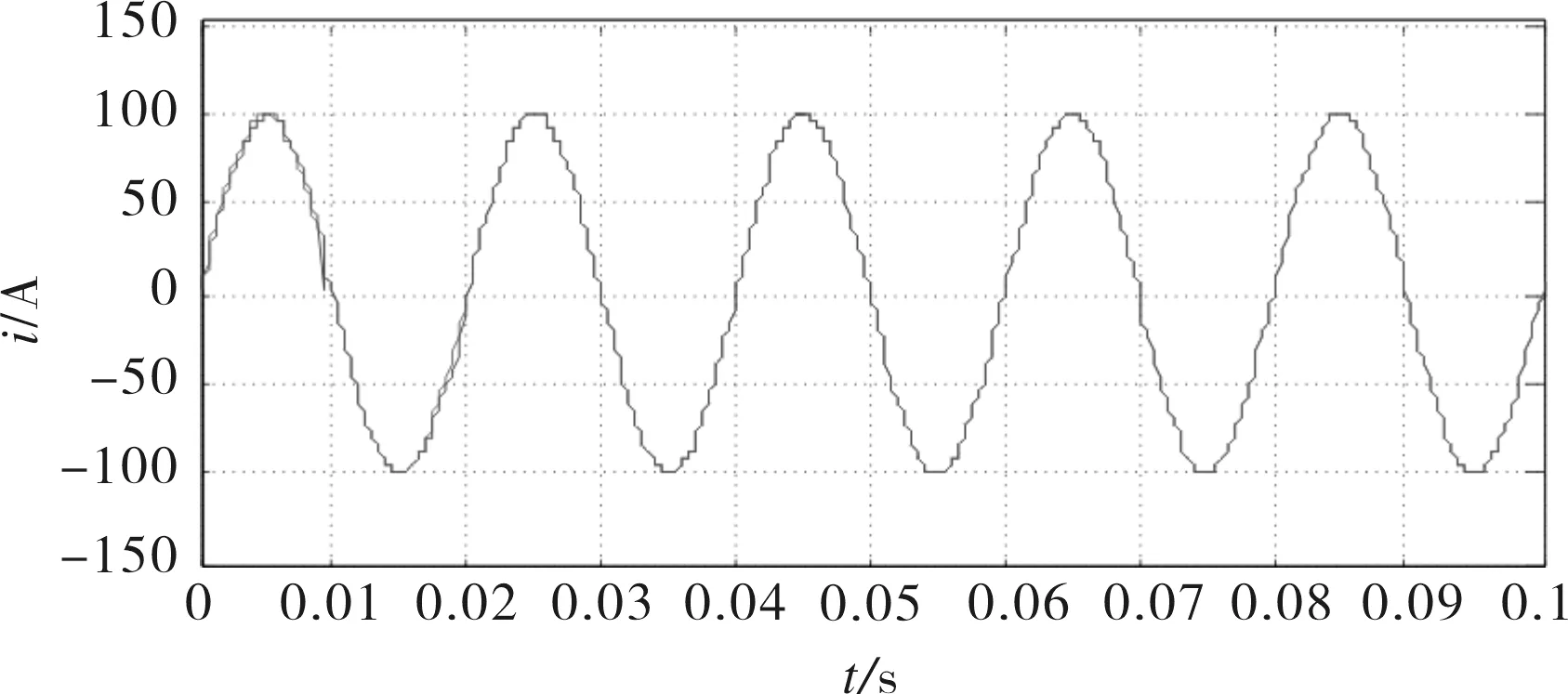
图3 基于RLS算法的谐波检测系统的跟随性能
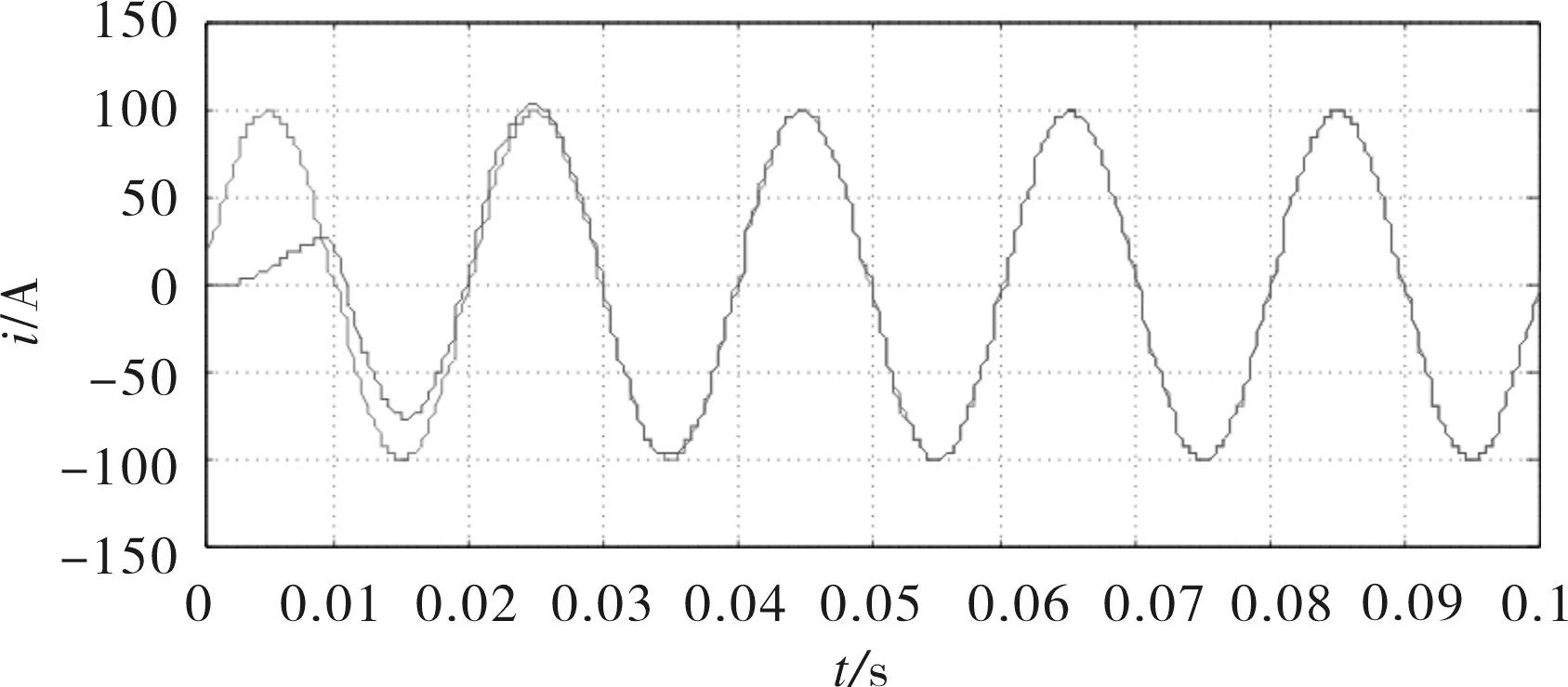
图4 基于变步长原理的谐波检测系统的跟随性能
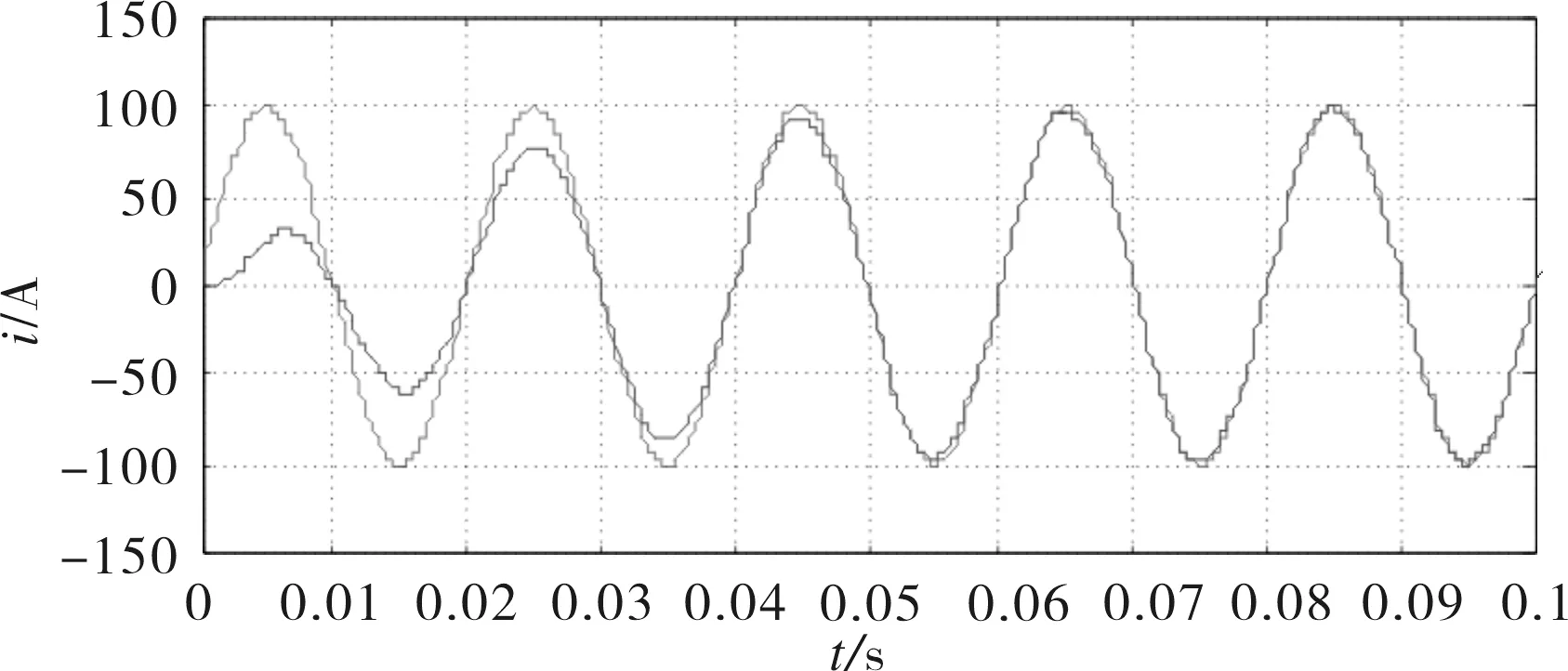
图5 基于对消原理的谐波检测系统的跟随性能
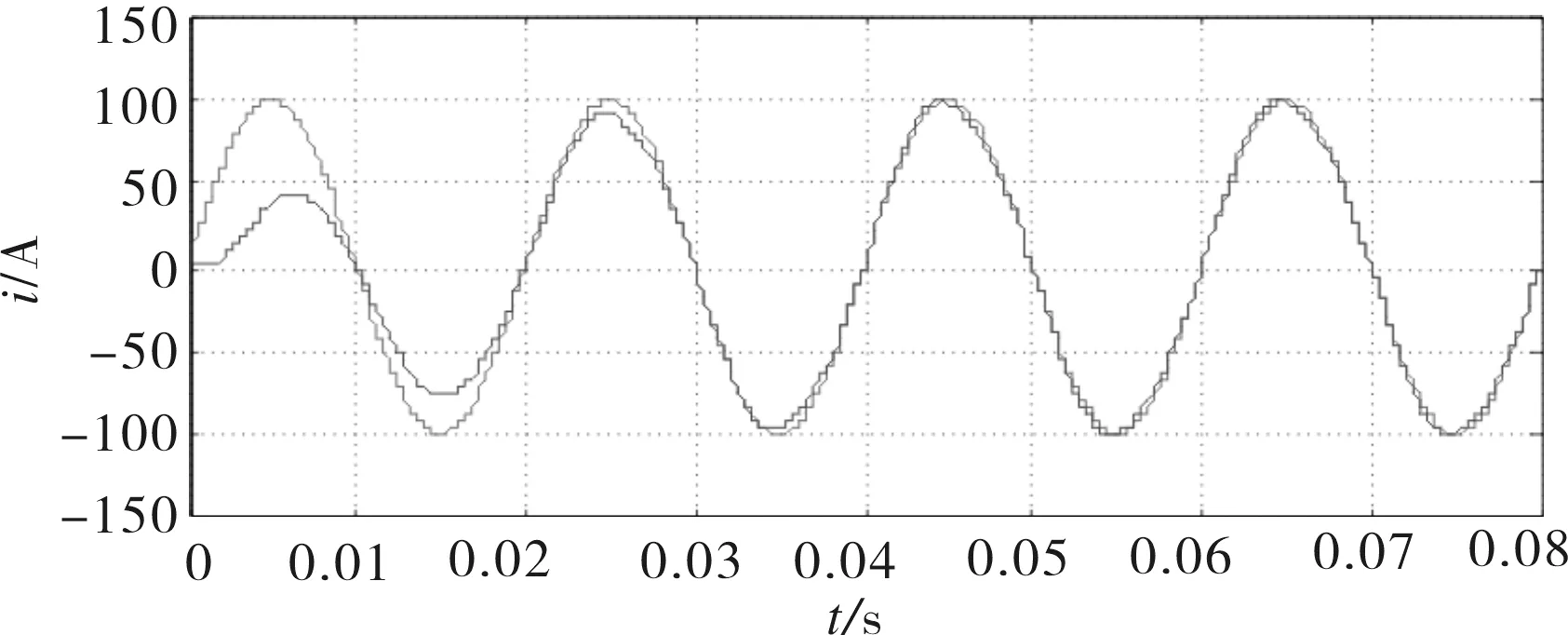
图6 模拟自适应方法的谐波检测系统的跟随性能
2.2 计算量与实现复杂度的比较
自适应算法中,若自适应滤波器的阶次为N,RLS算法每输入一个值需要(3N2+5N)次乘法,(2N2+3N)次加法得到一个新的输出;变步长方法中,每输入一个值需要经过(6N+2)次乘法和(3N+1)次加法得到一个新的输出;基于自适应干扰对消方法,每输入一个值需要经过(2N+2)次乘法和(2N)次加法得到一个输出.
在基于自适应类的谐波检测中,最常用的是基于对消原理的谐波检测方法,在对消原理中滤波器的阶次实际是一阶,可以看出,3种自适应方法中对消方法的计算量最少.
2.3 稳态精度的比较
自适应检测方法中的变步长检测方法按照文[26]中的参数来仿真,稳定后检测出谐波电流的畸变率(THD)为2.7%,同等条件下定步长对消LMS算法稳定后波形的THD 为2.4%,RLS算法稳定后波形的THD为1.1%,模拟电路检测方法稳定后波形的THD为3.2%.
2.4 自适应类基本方法的相互关系
在谐波检测的各类方法中,对于基波电流为标准正弦波还是跟电压波形相同一直存在争议.在FBD类检测方法中,如果电压畸变,那么得到的基波电流也是畸变的.
3 结语
本文对目前研究较多的4种基于自适应类谐波检测方法进行了深入的分析,以理论推导和仿真来说明这些方法的优缺点,给出各种不同方法的动态过程、时间滞后、计算量以及稳态精度等特性.旨在实际选择检测方法时提供参考.仿真结果表明,数字实现时,变步长检测方法过渡时间为1~2个周期;LMS对消方法的过渡过程为3~4个周期;RLS算法的过渡过程为1~2个周期;模拟电路实现时的过渡过程为2个周期.对消方法的计算量最小,RLS算法的畸变率最小.对于自适应类算法,由于参与运算的是sin和cos函数,无论电压是否畸变都能够准确地检测出谐波量.
参考文献
[1] 吴竞昌.供电系统谐波[M].北京:中国电力出版社,1998.
[2] 王兆安,杨 君,刘进军.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2004.
[3] Hammad A E.Analysis of second harmonic instability for the chateauguay HVDC/SVC scheme[J].IEEE Trans on Power Delivery 1992,7(1):410-415.
[4] Manchur G,Erven C C.Development of a model for predicting filter from electric arc furnaces[J].IEEE Trans on Power Delivery,1992,8(2):416-420.
[5] Alexander E E,John A O,David C,et al.A survey of harmonic voltages and currents at the customer′s bus[J].IEEE Trans on Power Delivery,1993,8(1):411-421.
[6] Luo Shiguo,Hou Zhencheng.An adaptive detecting method for harmonic and reactive current[J].IEEE Trans on Industrial Electronics,1995,42(1):85-89.
[7] Dxion J W,Garcia J J,Moran L.Control system for three-phase active power filter which simultaneously compensates power factor and unbalanced loads[J].IEEE Trans on Industrial Electronics,1995,42(6): 636-641.
根据现场地勘数据基坑周边土体参数见表2.土层划分较为复杂,为保证数据和结论的安全性,选用地质较差做为模拟参考,模型仅以标准段断面土层情况如图1所示,取标准段断面地勘报告大致划分土层信息,超过地勘资料以下土层均认为是中风化粉质砂岩.地勘资料提供的土体力学参数为压缩模量,模型中土体的弹性模量取压缩模量的2~3倍.根据建筑材料规范,钢支撑和钢围檩均为钢材在取值范围内取值.
[8] Hirofumi A.New trends in active filters for power conditioning[J].IEEE Trans on Industrial Application,1996,32(6):1312-1322.
[9] 朱鹏程,李 勋,康 勇,等.统一电能质量控制器控制策略研究[J].中国电机工程学报,2004,24 (8):67-73.
[10] 李战鹰,任 震,杨泽民.有源滤波装置及其应用综述[J].电网技术,2004,28(22):40-43.
[11] 唐 欣,罗 安,涂春鸣.基于递推型积分PI的混合有源滤波器电流控制[J].中国电机工程学报,2003,23(10):38-41.
[12] 张建辉,姜齐容,赵 地,等.有源滤波器控制器的设计[J].电网技术,2002,26(10):48-52.
[13] 孙 驰,魏光辉.基于同步坐标变换的三相不对称系统的无功与谐波电流的检测[J].中国电机工程学报,2003,23(12):46-51.
[14] Moran A L,Dixon J W,Rogel R.A three-phase active power filter operating with fixed switch frequency for reactive power and current harmonic compensation[J].IEEE Trans on Ind Electron,1995,42(4):402-408.
[15] 石 敏,吴正国,尹为民.基于RLS算法的时变谐波检测[J].电工技术学报,2005,20(1):50-52.
[16] Kwong R H,Johnston E W.A variable step-size LMS algorithm[J].IEEE Tran on Signal Processing,1992,40 (7): 1633-1642.
[17] 高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.
[18] 覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997,12(3):171-174.
[19] 李 辉,李亦斌,邹云屏,等.一种新的变步长自适应谐波检测算法[J].电力系统自动化,2005,29(2):69-73.
[20] 王 群,谢品房,吴 宁,等.模拟电路实现的神经元自适应谐波电路检测方法[J].中国电机工程学报,1999,19(6):42-46.
[21] 沈福民.自适应信号处理[M].西安:西安电子科技大学出版社,2001.
[22] 高大威.电力系统谐波、无功和负序电流综合补偿的研究[D].保定:华北电力大学博士学位论文,2001.
[23] 王 群,谢品芳,吴 宁,等.模拟电路实现的神经元自适应谐波电流检测方法[J].中国电机工程学报,1999,19(6):42-46.
[24] Akagi H,Kanazawa Y,Nabae A.Instantaneous reactive power compensators comprising switching devices without energy storage components[J].IEEE Trans on IA,1984,20(3):625-635.
[25] Luis A.A three-phase active power filter operating with fixed switching frequency for reactive power and current harmonic compensation[J].IEEE Trans on IE,1995,42(4):402-408.
[26] 李 乔,吴 捷.自适应谐波电流检测方法用于有源电力滤波器的仿真研究[J].电工技术学报,2004,19(12):86-90.

