卧式椭圆柱型储油罐的变位识别与罐容标定
王文发, 马 燕, 田云娜, 李红达
(1.延安大学计算机学院,陕西延安716000;2.延安大学软件研究与开发中心,陕西延安716000;3.中国科学院软件研究所信息安全国家重点实验室,北京100080)
为了适应陕北能源化工基地建设与发展的需要,持续提升石油企业核心竞争力,以陕北所属辖区石油企业为样本,在对其进行深入调研的基础上,分解构成生产成本的各主要环节,深入探究目前石油企业在生产管理中存在问题的根源,通过对存在问题根源进行科学的分析、研究,寻求问题的科学解释,建立相应的数学模型及求解算法,从而降低生产成本,优化部署生产及管理,提高企业经济效益和管理水平。笔者已经做了一些研究工作,并应用于陕北石油企业的生产实际中,效果良好。本文介绍其中一项工作——卧式椭圆柱型储油罐的变位识别与罐容标定模型及其解法,以及依据实际数据对模型的检验结果[1]。
1 问题描述
采油厂、炼油厂、集输站等石油企业都有很多不同形状、不同型号的地下储油罐,并且一般都有与之配套的油位计量管理系统。在理想状况下,即储油罐在不发生变位的情况下,通过储油罐在出厂时预先标定的罐容表(即罐内油位高度与罐内储油量之间的对应关系)进行实时计算,即可得到储油罐罐内油位高度和储油量的变化情况。
但实际上,储油罐在安装时很难做到理想状况,特别是使用一段时间后,由于温度变化、地基变形等原因,使罐体的位置产生纵向倾斜和横向偏转等变化(称为变位),从而导致罐容表读取数据和实际数据不吻合,甚至偏差很大,造成计量误差。因此必须定期对储油罐的变位情况进行识别,及时对罐容表进行重新标定。
本文对两端平头的椭圆柱体的储油罐(见图1)变位后罐内油量进行重新标定,建立相应的标定模型,给出储油罐在水平和倾斜放置时的罐容标定公式。

Fig.1 The diagram of eliptical cylinder tank with two flat ends图1 两端平头的椭圆柱体储油罐示意图
2 问题分析
该问题的本质是当储油罐发生变位后如何重新标定罐内油量与油位探针之间的对应关系,对于一个储油罐而言,变位前后的罐内储油量是不发生变化的,因此,解决问题的关键首先是如何计算储油罐在未发生变位情况下的罐内储油量与油位探针指示高度间的关系,然后根据储油罐出厂时预先标定的罐容表(即罐内油位高度与储油量的对应关系)对储油罐在未发生变位情况下,罐内储油量与油位探针指示高度间的关系进行调整,使其与真实值尽可能一致,最后根据变位前的油位探针指示高度与变位后的油位探针指示高度、纵向倾斜角和横向偏转角间的对应关系,对变位后的储油罐罐内油量与油位探针指示高度进行重新标定[2-3]。
3 模型建立
确定油罐无变位时油罐储油量与罐内油位高度之间的关系,当罐体无变位时,罐内储油量的体积形状是规则,如图2所示。
为了计算两端平头椭圆柱体储油罐罐内所储油量对应的体积V,建立如图3所示的坐标系。
根据积分的概念并结合图3,有体积元素:
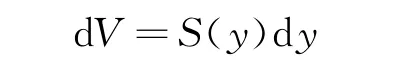
其中S(y)dy表示垂直于xoy平面的截面来切割两端平头椭圆柱体;S(y)=2xL


Fig.2 The diagram of elliptical cylinder no changed position图2 两端平头的椭圆柱体未变位示意图

Fig.3 The coordinate system of elliptical cylinder transverse section图3 椭圆柱体截面坐标示意图
于是就有两端平头椭圆柱体罐内油量V就等于在油罐长度L上给油的横截面积S积分,如下所示:
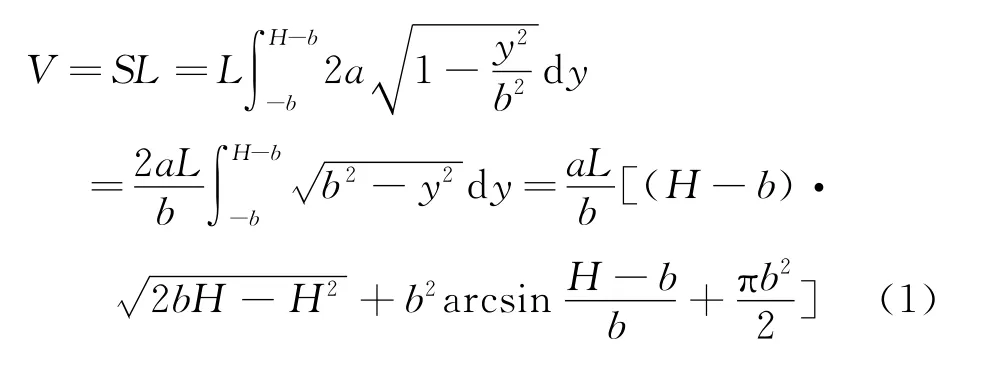
由于(1)式关于储油罐罐内油量的计算是严格按照规则几何图形进行的,而实际中储油罐不可能是完全标准的几何图形,因此需要对其进行必要修正,设储油罐出厂时在油位探针高度为H时的罐内油量标定为V′,则调整后的罐内油量计算公式为:

其中f(H)为罐内储油量的实际值与理论值之差,是关于油位探针指示读数的函数,在实际中,可以将H按照一定的变化高度(如0.1cm),通过计算V与V′的差值得到H与f(H)的调整表[4-5]。
两端平头椭圆柱体发生横向转动的可能性很小,因此对于两端平头椭圆柱体储油罐发生变位的情况主要考虑纵向移位的情况,如图4所示。

Fig.4 The longitudinal section of elliptical cylinder changed position图4 两端平头的椭圆柱体纵向变位截面图
容易得出H1与H的关系式为:H1-H=tanα(L/2-l)。整理得:

将(1),(3)式带入(2)式得到两端平头椭圆柱体变位后罐内油量与油位探针指示高度的标定模型,即:

对于(4)式的标定模型,其关键是如何确定纵向倾角α。
确定α的具体解决方法如下[6]:
1)获取每次实际进、出油量Vi和油位探针高度Hi,i=1,2,…,n;
2)计算得到实际储油量的改变量ΔVi=F(α,H1)-F(α,Hi+1);
对于上面给出的标定模型,只要能够确定出α,用(3)式和(2)式的关系,就能得出H1和V′的对应关系,即实现储油罐变位后的重新标定。但是(3)式的成立是有条件的,下面给出(3)式成立的范围,如图5所示[7]。
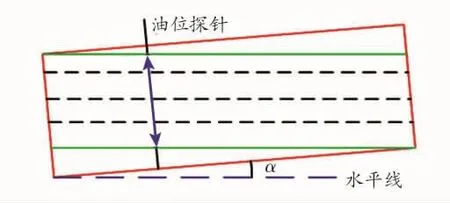
Fig.5 The longitudinal section of elliptical cylindertank changed position图5 两端平头的椭圆柱体储油罐纵向变位截面图
容易证明,(3)式成立的条件必须满足储油罐罐内储油量等于或高于下绿线指示高度且低于或等于上绿线指示高度,即:H1∈[(L-l)tanα,b-ltanα]。
4 实现步骤
对储油罐变位实现重新标定的具体步骤如下[8-9]:
1)根据油罐出厂时所标定的罐内油位高度与罐内储油量之间的对应关系,确定出储油罐的调整表,即f(H)与H的对应表;

3)依据前面所建立储油罐变位后罐内油量重新标定模型(已知纵向倾斜角α和横向偏转β、储油罐油位探针H1或H2,H与H1或H2的对应关系、第一步所得到的f(H)与H的对应关系)实现对变位油罐罐内油量的重新标定。
5 模型检验
根据某集输站储油罐变位前后罐容变化的实际测量数据得到如图6所示的h和ΔV(h)的拟合曲线,从图6中可以看出变位对罐容表的影响是比较大的。
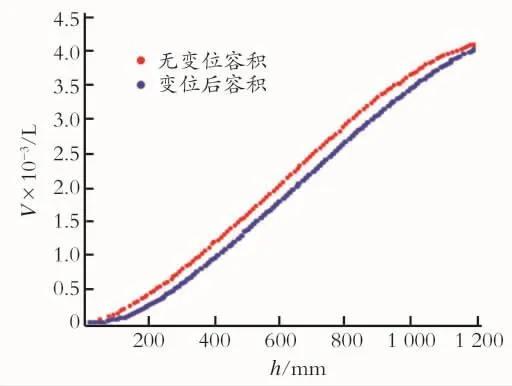
Fig.6 The fitting curves of handΔV(h)图6 h和ΔV(h)的拟合曲线
将200个储油罐实际测量数据与模型理论计算值在同一图中进行比较,结果如图7所示,吻合得非常好,说明了模型的可行性和正确性。
同时对重新标定前后的数据进行误差分析,结果表明:重新标定前,当h较小时误差较大,接近10%;当h较大时误差较小,误差范围在2.34%到4.65%;重新标定后,相对误差在0.22%到0.67%范围内,平均误差为0.445%。因此,本文的重新标定方法确实提高了储油罐变位后罐容表标定值的精度。
6 结束语
本文从实际应用入手,对卧式平头椭圆柱型储油罐变位后罐内油量进行重新标定,建立相应的标定模型,给出了储油罐在水平和倾斜放置时的罐容标定公式。结合实例通过实际数据对模型进行检验,检验结果验证了模型的正确性。值得注意的是,在使用储油罐变位后罐内油量重新标定模型时,对于H1或H2均有一定的范围,但是在实际问题中,由于α与β均比较小,且储油罐不会出现满罐和罐内无油的情况,因此上述模型具有较高的应用价值。但是,本模型所考虑的条件仍然是比较理想化的状态,事实上储油罐在地下形变的情况较为复杂,如何有效准确进行标定仍然值得我们进一步研究。

Fig.7 The comparison curves of actual measurement data and theoretical calculated value图7 变位后实际测量数据与模型理论计算值的比较
[1] 祝英杰.储油罐的变位识别与罐容表标定[J].长春大学学报,2011,21(2):55-58.
[2] 凌佳.定积分在储油罐的变位识别与罐容表标定中的应用[J].牡丹江大学学报,2011,20(4):119-121.
[3] 刘田.储油罐的变位识别与罐容表标定[J].四川兵工学报,2011,32(2):65-68.
[4] 侯超钧.倾斜带封头卧式储油罐的罐容标定[J].贵州师范大学学报,2011,29(2):94-98.
[5] 杨德志.储油罐的纵向变位识别与罐容表标定[J].赤峰学院学报,2011,27(2):19-22.
[6] 郜欣春.储油罐发生纵向倾斜时罐容表的重新标定[J].河南科学,2011,29(3):354-356.
[7] 徐德华.椭圆头立罐装量与液位的算法和模拟[J].实验科学与技术,2010,8(2):22-26.
[8] 伍人暾.关于储油罐内液体数量的技术分析[J].广州化工,2011,39(7):144-146.
[9] 王妍玲.椭圆形封头卧式贮罐液位与容积对应关系的建立[J].齐齐哈尔大学学报,2002,18(1):88-90.

