讨价还价下供应链批发价格契约参数分析及实验研究

林 强，赵光香，吴 飞

(天津大学管理与经济学部，天津300072)

供应链多是由利益相对独立的多个企业通过联盟或合作关系组成的分散式供应链，系统联合最优的决策对各个成员来说往往不是最优的，当供应链的各成员都试图最优化自己的利润，供应链整体的利润将不可避免的受到损害，出现所谓“双重边际效应”和“牛鞭效应”，如何使供应链上的企业风险共担、利益共享，提高供应链的核心竞争力是供应链研究的核心。近年来，研究通过供应链契约协调机制来约束和协调供应链上的各个个体，提高供应链系统的绩效，达到参与方共赢，已成为供应链管理的一个新的热点。

一、批发价格契约的研究现状

批发价格契约是指零售商根据市场需求和批发价格决定订购量，供应商根据零售商的订购量组织生产，零售商负责处理剩余产品，因此，该契约中供应商的利润是确定的，零售商完全承担市场风险［1］。

Lariviere和Poteus对批发价格契约进行了详细的研究，分析了报童模型情况下批发价格契约的供应链协调问题。他们研究发现在批发价格契约模式下，只有在供应商制订的批发价不高于其制造成本的前提下，供应链效率才能够达到最优。他们还发现制造商的利润和销售数量随需求的增长而相应增加，但是批发价格依赖需求的增长方式。文章还进一步研究了当零售商参与了市场预测或是拥有机会成本而地位强化时，生产商会降低批发价，从而提高系统总利润的情况［2］。Tilson等基于Lariviere等考察的报童模型，在供应商处于Stackelberg博弈中，领导者地位且供应商完全了解零售商的成本和收益函数的假设下，分析了批发价格契约的单调性问题，当供应商的生产成本提高时，均衡批发价格会略微提高，但是当零售商的成本提高时，均衡批发价格则有可能提高也有可能降低。随着供应商或零售商的成本提高，供应商的利润会略有下降［3］。叶飞等研究了一类由供应商与分销商组成的两级供应链在弹性需求下的协作机制设计问题，提出了一种基于不对称Nash协商模型的批发价格契约机制来协调合作双方的收益，并进行了数据模拟与综合分析［4］。刘海军等通过引入合作博弈条件下讨价还价问题的K-S解作为一个合理分配机制，对双方合作后获得的新增利润进行了分配，得到分配结果使得双方利润比不合作时均有所提高的结论［5］，该文的研究方法主要是通过构建相关模型展开分析，与本文的研究方法不同。另外，在所获得的结论上也有差异。慕永国等构建了批发价格契约和二次订购契约最优订购量的均值－CVaR模型。通过算例分析，在综合考虑供应链的收益及极端风险事件对收益的影响后，二次订购契约在获得更高收益的同时能够降低收益的风险［6］。

二、讨价还价基本模型分析

1.鲁宾斯坦轮流出价模型

两个参与人A和B，分割大小为π(其中π＞0)的蛋糕进行讨价还价，直到有一个参与人接受了一个出价为止。

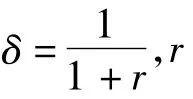
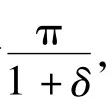
2.纳什讨价还价模型

(一)三回合的讨价还价博弈

三回合的讨价还价可以采用博弈树来表示(见图1)。

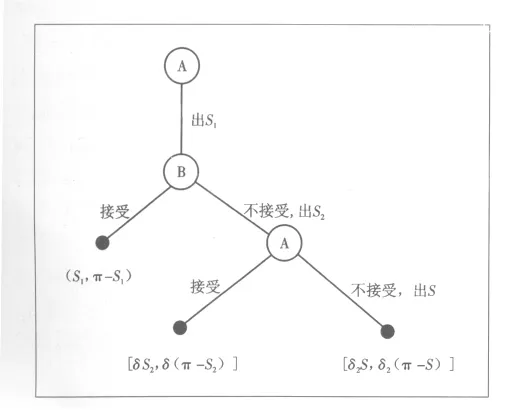
图1 三回合讨价还价博弈

采用逆推归纳法来分析该博弈，即在第三阶段，A出S，B必须接受，双方得益分别为δ2S和δ2(π－S);在第二阶段，B知道A在第三阶段必出价S，而且自己必须接受，而对方在第二阶段能够接受的S2必须满足δS2≥δ2S，即S2≥δS。因此，B会提出S2=δS，B所得为δ(π－S2)=δ(π－δS)，比第三阶段能得到δ2(π－S)的更多，这是第二阶段的最优方案。

同理，A在第一阶段出S1*=π－δ(π－δS)是最优的。

这样，这个三阶段讨价还价博奔的子博弈完美纳什均衡是A在第一阶段提出分配方案［π－δ(πδS)，δ(π－δS)］，B接受。

(二)无限回合讨价还价博弈

三、供应链批发价格契约及经济实验研究

1.批发价格契约模型及假设条件

(一)供应链模型分析及相关参数含义

本文考虑一个供应商和一个零售商组成的二级供应链，如图2所示。零售商面临一个随机的市场需求，且假设供应商是领导者，零售商是追随者，供应商给出自己的一系列契约参数后零售商据此选择最优订购量q。假设单位产品的生产成本为c，单位产品的零售价格为p，单位产品的批发价格为w，零售商的订购量为q，销售期末产品对零售商的剩余价值为0，供应商可以选择回购剩余产品。零售商面临不确定需求D，其概率分布函数及密度函数为F(x)和f(x)，且F(x)可微、单调递增，F(0)=0。假设需求D服从［0，1］的均匀分布。同时假设供应商的生产能力是无限的，且不考虑生产提前期。市场是完全开放的，即供应商和零售商互相了解对方的成本及价格信息。供应链成员都是风险中性和完全理性的，根据期望利润最大化进行决策。模型其他参数含义说明如下:πT为供应链的期望总利润;πR为零售商的期望利润;πS为供应商的期望利润;S(q)为零售商的期望销售量。

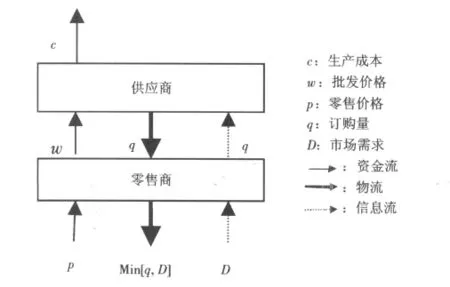
图2 供应商和零售商组成的二级供应链

假设在销售周期开始前，零售商可以得到关于零售价格的信息，这就可以通过对市场预测和前期销售数据得到。单位产品的生产成本是已知的，讨价还价时的贴现因子是已知的，而且以上信息对于供应商和零售商是相同的。如果需要讨价还价，则在销售周期开始前讨价还价。讨价还价结果分两种情况:一是讨价还价破裂，双方在销售周期内各自以自己的最大收益为目标，确定批发价格和订购量;二是讨价还价达成，双方按照讨价还价后的收益联立方程求出最优批发价格和最优订购量。

(二)批发价格契约不讨价还价理论模型

零售商利润πR=pS(q)－wq;供应商利润πS=(w－c)q;供应链总利润πT=πR+πS=pS(q)－cq。

对πT、πR求最大，得到

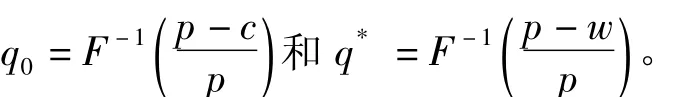
为了使供应链协调，有w=c，即供应商利润为0，有悖于常理，不进行讨价还价时无法实现供应链协调。

(三)批发价格契约进行讨价还价理论模型

在不确定需求实现之后，对批发价格讨价还价，利用Rubinstein的基本轮流出价模型，供应商先出价。

2.实验研究及其结论

在供应链管理实验方面，王冬良、郑平做了基于第三方物流业务模型的供应链管理实验设计，文章主要通过对第三方物流公司的考察，结合新技术的发展，对新形势下的供应链管理实验进行了探索和设计［8］。Elena Katok和Diana Yan Wu做过供应链协调契约的管理实验，文章主要对三种契约批发价格契约、回购契约、收益共享契约进行实验，并把实验结论和理论进行了比较［9］。

限于篇幅，本文仅对批发价格契约展开实验研究，假设如果讨价还价破裂，则参与者双方将得到不讨价还价时的收益。本文实验的目的是通过实验得到在批发价格契约下不讨价还价和讨价还价两种情况哪种给双方带来的收益更大，为以后供应商和零售商在签订契约决策时做参考。将讨价还价过程用QT程序设计语言实现［10］。

(一)实验过程

供应商第一回合先出价S1，满足a＜S1＜πT*，如果－S1≥b，讨价还价过程结束，从而得到πS=S1，πR=－S1;如果πT*－S1＜b，则进行第二回合。

零售商第二回合先出价S2，满足b＜πT*－S2＜，如果δ(πT*－S2)≤b，讨价还价的过程结束，得到πS=a，πR=b;如果δ(πT*－S2)＞b and δS2≥a，讨价还价过程结束，得到πS=δS2，πR=δ(πT*－S2);如果δ(πT*－S2)＞b and δS2＜a，则进行第三回合。

供应商第三回合先出价S3，满足a＜S3＜πT*，如果δ2S3≤a，讨价还价过程结束，得到πS=a，πR=b;如果δ2S3＞a and δ2(πT*－S3)≥b，讨价还价过程结束，得到πS=δ2S3，πR=δ2(πT*－S3);如果δ2S3＞a and δ2(－S3)＜b，则进行第四回合。

假设进行到第N回合:当N是偶数时，零售商先出价SN，满足b＜πT*－SN＜πT*，如果δN－1(πT*－ SN)≤b，讨价还价过程结束，得到πS=a，πR=b;如果δN－1(πT*－SN)＞b and δN－1SN≥a讨价还价过程结束，得到 πS=δN－1SN，πR=δN－1(πT*－SN);如果δN－1(πT*－SN)＞b and δN－1SN＜a则进行第N+1回合。当N是奇数时，供应商先出价SN，满足a＜SN＜，如果δN－1SN≤a，讨价还价过程结束，得到πS=a，πR=b;如果δN－1SN＞a and δN－1(πT*－SN)≥b，讨价还价过程结束，得到π=δN－1S，π=δN－1(π*SNRT－SN);如果δN－1SN＞a and δN－1(πT*－SN)＜b，则进行第N+1回合。

以此延续下去。将具体数值代入依据上述步骤编程后得到的谈判模拟器中，得到一次多轮讨价还价的实验结果，如图3所示。

图3 实验过程与结果

(二)实验结论

(1)在讨价还价情况下，供应链的总收益可以达到最优，供应商和零售商的收益也分别大于不讨价还价情况下的收益。通过建立供应商和零售商的收益函数模型，可以解出最优批发价格w*和最优订购量q*。

(2)讨价还价下的批发价格契约可以实现供应链协调，但这与供应商和零售商在讨价还价时的出价有关。在讨价还价情况下，根据供应商和零售商的出价，讨价还价达成，双方按照讨价还价后的收益联立方程求出最优批发价格和最优订购量，这时的批发价格契约可以任意分割供应链的总收益，且供应链的总收益达到最优，故讨价还价下的批发价格可以实现供应链协调。

(3)本文只进行了一次多轮讨价还价过程的实验研究，其研究结论仅局限于供应链中企业间只有一次交易的情况。在应用本文实验方法进行多次多轮博弈实验后，结论如何将在后续研究中作为重点内容给予阐述。

四、结 语

本文构建了由单一供应商与单一零售商组成的两级供应链，研究了在批发价格契约下，运用讨价还价理论解决参数设计问题，运用实验设计的方法对模型进行了检验。从研究结果来看，在多轮讨价还价方式下，供应链的总收益可以达到最优，供应商和零售商的收益也分别大于不讨价还价情况下的收益。讨价还价下的批发价格契约可以实现供应链协调，但与供应商和零售商在讨价还价时的出价有关。下一步研究的重点是通过大量的人-机博弈实验，采用统计分析法，获得供应商和零售商在讨价还价过程中的出价规律以及收益曲线，得出平均价格及与之相关的收益曲线，为实际应用建立基础。

［1］ 杨德礼，郭 琼，何 勇，等.供应链契约研究进展［J］.管理学报，2006，3(1):117-125.

［2］ Lariviere M A，Porteus E L.Selling to the newsvendor:An analysis of price-only contracts［J］.Manufacturing and Service Operations Management，2001(4):293-305.

［3］ Tilson V，Monotonicity.Properties of wholesale price contracts［J］.Mathematical Social Sciences，2008，56(1): 127-143.

［4］ 叶 飞，李怡娜，符少玲.弹性需求条件下供应链协作的批发价格机制研究［J］.工业工程，2006，9(5):18-22.

［5］ 刘海军，陈菊红，王能民.基于合作博弈K-S解的供应链批发价格协调机制的实现［J］.统计与决策，2009，20:51-53.

［6］ 慕永国，麦 强，冯英浚.供应链价格契约的均值－CVaR模型［J］.哈尔滨工业大学学报，2009，41(12):298-300.

［7］ 管毅平，郑丹秋.讨价还价理论及其应用［M］.上海:上海财经大学出版社，2005:31-37.

［8］ 王冬良，郑 平.基于第三方物流业务模型的供应链管理实验设计［J］.网络财富，2009(4):28-29.

［9］ Elena Katok，Diana Yan Wu.Contracting in supply chain: A laboratory investigation［J］.Management Science，2009: 10.

［10］ 吴 飞.讨价还价模型下洪应链相关契约分析与实验研究［D］.天津:天津大学管理学院，2010.