乘潮潮位的理论分布探讨*

董 胜,曹书军,周 冲,吴成利

(1.中国海洋大学工程学院,山东青岛266100;2.胜利油田森诺胜利工程有限公司,山东东营257000)

在港口工程中,当考虑乘潮作业时(如船舶乘高潮进出港口、乘低潮施工),需要统计确定乘潮潮位的累积频率,其步骤如下:

(1)当考虑船舶进出港口时,首先须确定乘潮所需持续时间t。

式中,Lk表示航道长度,v为航道内允许航速;k为时间富裕系数,可取1.1～1.3。

(2)在潮位过程线上,量取各次潮峰上的历时等于t的潮位值,统计其在不同潮位级的出现次数。

(3)一般采用10 cm为一级,对潮位分级。

(4)由高到低逐级进行累积出现次数的统计。

(5)计算各潮位级的累积频率p,公式如下:

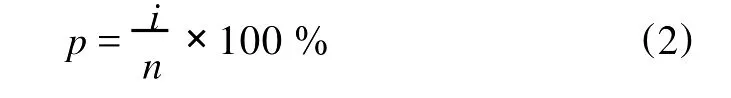
式中,i为各潮位级相应的累积出现次数;n为高潮位总次数。

(6)在方格纸上,以纵坐标表示潮位,以横坐标表示累积频率,把各累积频率值点于相应潮位级的下限处,连绘成高潮位累积频率曲线。

(7)读取累积频率为75%的潮位,即为所需的高潮乘潮潮位。

如系计算低潮乘潮历时t为2 h,累积频率为80%的低潮乘潮施工水位,则应将第2步改为“在潮位过程线上,量取各次潮谷上的历时2 h的潮谷值”,同时,在计算低潮乘潮作业水位时,系指低于该潮位所占的累积频率,其余统计步骤与高潮乘潮水位的相同。

上述传统的方法在绘制累积频率曲线时,缺乏理论分布模型,累积频率曲线是用手工的办法,根据观测潮位散点的趋势绘制完成的[1],所以,得到的乘潮潮位值因人而异,存在主观任意性。本文将探讨最大熵分布在乘潮潮位统计中的适用性,为乘潮潮位数据的自动化处理探索有益的途径。

1 最大熵分布

1975年U lrych等将最大熵原理应用在海浪的谱分析中[2];1996年,吴克俭等将该原理应用于海浪波高的统计分布,指出Rayleigh分布为理想状况下,波高达到最大混乱程度时必然遵循的1种分布,但若用于描述实际波浪则有偏差,更提出Weibull分布为某些约束条件下的最大熵分布的特殊形式[3];徐福敏于2000年推导出二阶矩意义下的最大熵概率密度分布表达式,并由最大熵法得到了深水充分发展波波高概率分布及风浪槽试验中不同水深时的波高概率分布[4];Xu Delun等于2004年推导出非线性海浪波高的最大熵分布,并将其应用于多年一遇海洋要素估计[5];随后,周良明等指出了波高熵与波浪的状态参量及平均波高的关系,将最大熵分布与广泛应用的瑞利分布作了比较并指出最大熵分布具有明显的优越性[6]。Zhang Lizhen等提出了1种描述非线性波高的新型最大熵分布[7]。董胜等提出了泊松最大熵分布,并将其用于计算台风海浪的重现值波高[8]。

在推导最大熵分布的过程中,Xu Delun等提出适用于海洋环境中的约束条件,并推导得到了适用于描述于描述海洋工程环境条件的最大熵分布密度函数为[5]。约束条件如下:

代入Euler方程,并令α′=-1-λ1,β=λ3,γ=-λ2,可得最大熵分布的概率密度函数为[11]:

为了拟合港口工程的乘高(低)潮潮位的实测资料,在此引入位置参数a0,由式(4)可得改进的最大熵分布

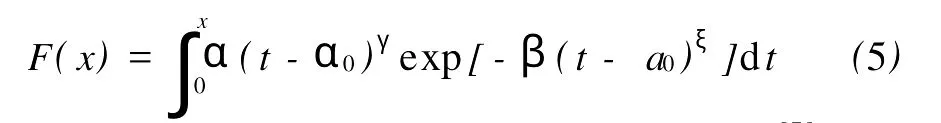
Zhang Lizhen等给出了求解式(5)的矩法[7]。参照工程水文中Pearson-Ⅲ型分布求解的经验适线法[9],本文采用此法来估计最大熵分布的未知参数。

经验适线法是水利与海洋工程中普遍采用的进行极值频率分析的方法之一。这种方法根据工作者的经验,不断调整参数,使目估认为拟合最佳为止。随着计算技术的发展,目估已由最佳适线准则与电算替代。

具体计算时,一般认为观测值序列的均值比较稳定,误差较小,可用矩法估计。离差系数Cv的初值也可用矩法初算,并设定若干个偏态系数Cs,进行试错适线,逐步调整Cv与Cs这2个参数,直至观测点均匀分布在理论分布曲线的两侧。

为了估计改进最大熵分布的参数,本文选取理论分布频率与经验频率的离差平方和最小为适线准则,来确定拟合观测值的最佳分布函数。

将式(4)代入式(3a),可得

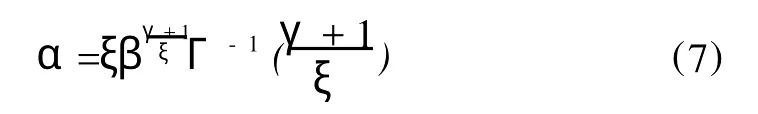
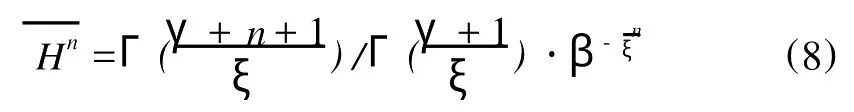
将式(8)代入式(6)可得

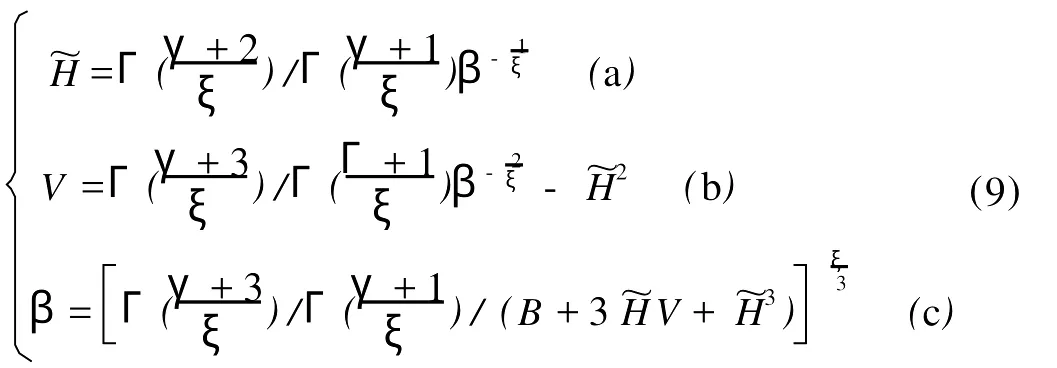
联立式(9a)与(9b)、式(9a)与(9c),消去β可得

对改进的最大熵分布进行拟合时,经验适线法的过程如下:

①首先由样本求出Cv值,选取不同的k得到Cs=k·Cv;

②改变k和a0,限定ξ在某范围内有意义,代入式(10),可以得出对应的γ值;

③进而由式(9)和(7)求出α和β,得到不同的参数组对应的改进最大熵分布密度函数;

④计算最大熵分布的概率值与经验概率值的平均离差平方和Q,以使离差平方和Q最小为标准所求得的参数即为所求的参数,相应的分布函数即为所求分布函数。

2 工程应用

按《海港水文规范》规定,确定乘潮高(低)潮位时,应有完整的1 a或多年的实测潮位资料,绘制累积频率曲线,在其上选取所需的累积频率潮位值。

2.1 威海湾乘潮潮位

选取威海湾1992年的验潮资料,进行了乘高、低潮2 h频率分析,手工绘制求得了乘2 h高潮位值计算结果见表1。

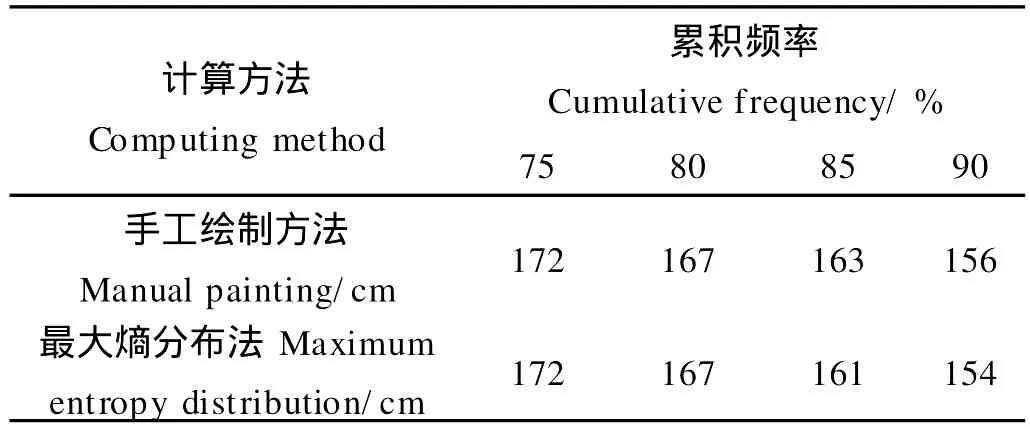
表1 威海湾2 h乘高潮潮位Table 1 Ridable high tidal level at Weihai Bay

采用最大熵分布,对乘高潮潮位的数据进行拟合,其统计直方图见图1,累积分布曲线如图2,计算得出乘高潮潮位值见表1。此结果与手绘累积率曲线得到的结果基本相等,最大相差2 cm。说明最大熵分布对威海湾乘高潮潮位的分布是适用的。

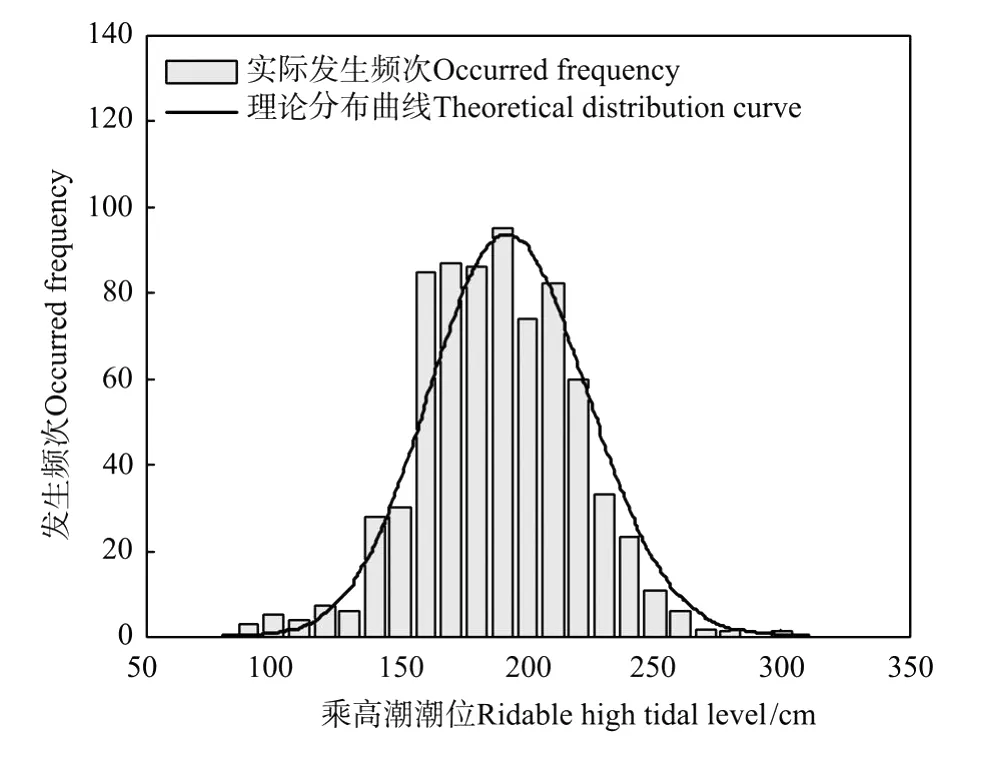
图1 威海湾乘高潮潮位统计直方图Fig.1 Histogram of ridable high tidal level at Weihai Bay

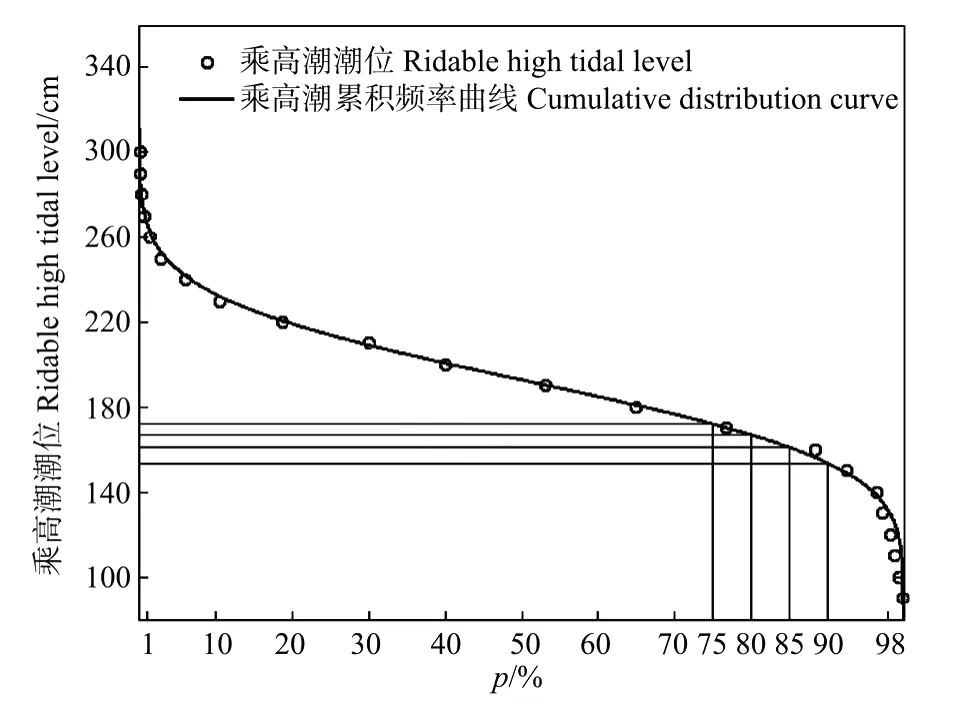
图2 威海湾乘高潮最大熵分布拟合Fig.2 Maximum entropy distribution fitting for ridable high tidal level at Weihai Bay

同样选取威海湾1992年的验潮资料,进行了乘低潮2 h频率分析,求得了乘2 h的低潮位值计算结果见表2。

采用最大熵分布,对乘低潮潮位的数据进行拟合,其直方图见图3,累积分布曲线如图4,计算得出乘低潮潮位值见表2。此结果与手绘累积率曲线得到的结果基本相等,最大相差1 cm。说明最大熵分布对威海湾乘低潮潮位的分布也是适用的。

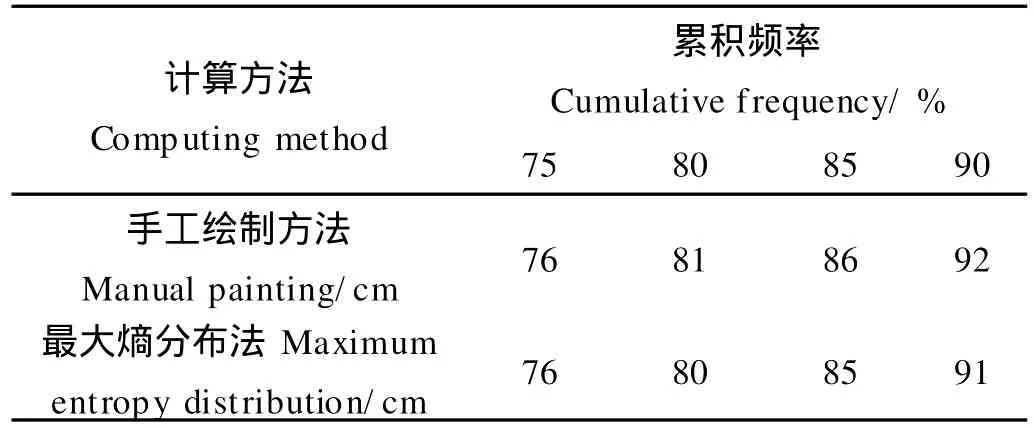
表2 威海湾2 h乘低潮潮位Table 2 Ridable low tidal level at Weihai Bay

图3 威海湾乘低潮潮位统计直方图Fig.3 Histogram of ridable low tide level in Weihai Bay

图4 威海湾乘低潮最大熵分布拟合Fig.4 Maximum entropy distribution fitting for ridable low tidal level at Weihai Bay

2.2 胶州湾乘潮潮位

再选取胶州湾1966年的验潮资料,进行了乘高、低潮2 h频率分析,手工绘制求得了乘2 h高潮位值计算结果见表3。

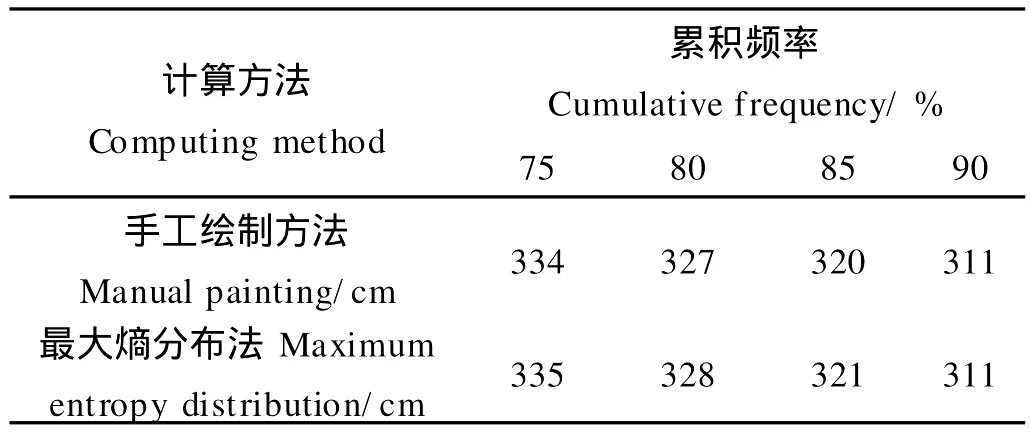
表3 胶州湾2 h乘高潮潮位Table 3 Ridable high tidal level at Jiaozhou Bay

采用最大熵分布,对乘高潮潮位的数据进行拟合,其统计直方图见图5,累积分布曲线如图6,计算得出乘高潮潮位值见表3。此结果与手绘累积率曲线得到的结果基本相等,最大相差1 cm。说明最大熵分布对胶州湾乘高潮潮位的分布是适用的。

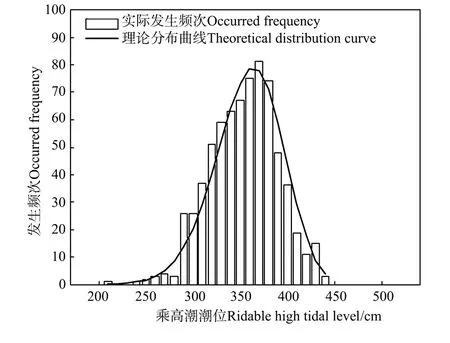
图5 胶州湾乘高潮潮位统计直方图Fig.5 Histogram of ridable high tidal level at Jiaozhou Bay

图6 胶州湾乘高潮最大熵分布拟合Fig.6 Maximum entropy distribution fitting for ridable high tidal level at Jiaozhou Bay

同样选取胶州湾1966年的验潮资料,进行了乘低潮2频率分析,求得了乘低2 h的潮位值计算结果见表4。

表4 胶州湾2 h乘低潮潮位Table 4 Ridable low tidal level at Weihai Bay

采用最大熵分布,对乘低潮潮位的数据进行拟合,其直方图见图7,累积分布曲线如图8,计算得出乘低潮潮位值见表4。此结果与手绘累积率曲线得到的结果基本相等,最大相差3 cm。说明最大熵分布对胶州湾乘低潮潮位的分布也是适用的。

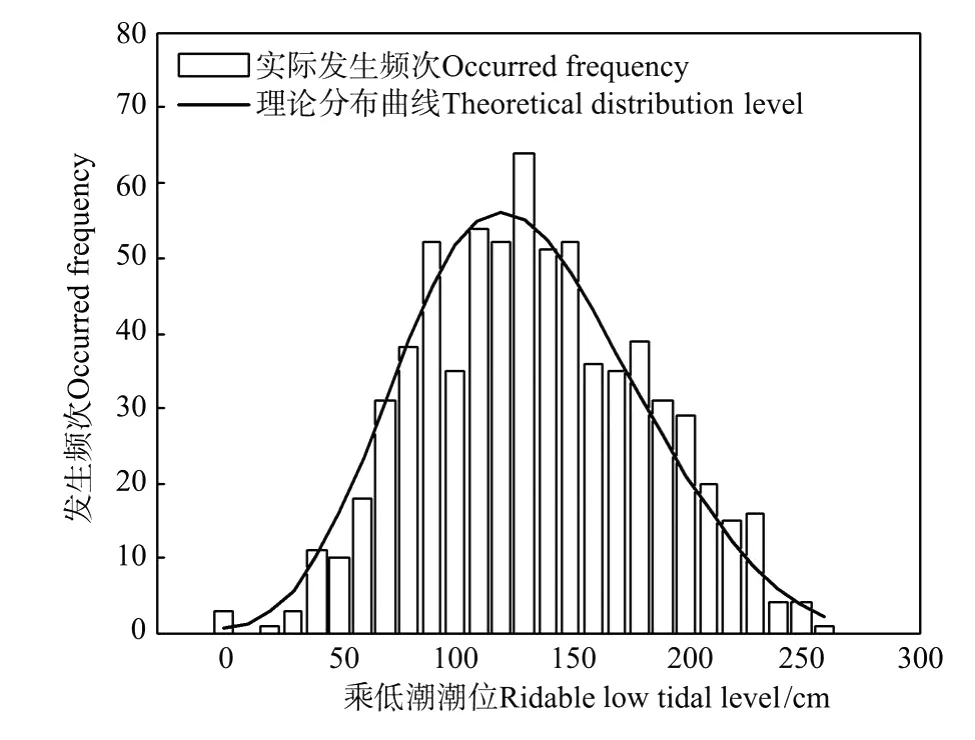
图7 胶州湾乘低潮潮位统计直方图Fig.7 Histogram of ridable low tidal level at Jiaozhou Bay

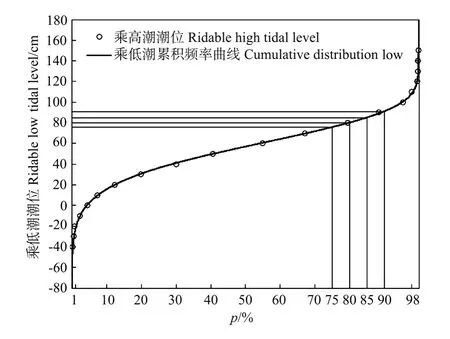
图8 胶州湾乘低潮最大熵分布拟合Fig.8 Maximum entropy distribution fitting for ridable low tidal level at Jiaozhou Bay

2.3 计算结果比较分析

由以上2个算例可以看出,最大熵分布曲线与实测数据吻合较好,计算得到的设计潮位精度高,说明最大熵分布是适用于工程设计潮位推算的理论曲线。

在确定乘低潮潮位时,目前有些文献存在对定义的误解,主要有以下2种:

①有文献在绘制乘低潮潮位累积频率曲线时,采用从大到小的对潮位进行分级排列,然后读取75%累积率的潮位值作为乘低潮潮位[10]*。这种方法确定的是高于某累积率的值,而非低于某累积率的值,显然是错误的。

②对于乘低潮潮位,仍然按照方法①进行潮位的分级排列,是否可以读取25%的潮位来表示乘潮低潮位值呢?答案也是否定的。以胶州湾乘低潮潮位的最大熵分布为例,其实测潮位序列的平均值为133 cm,而Cs值为0.0876,由图9可见,最大熵分布的概率密度曲线是左偏的,因此,低潮位从小到大的累积率75%对应的潮位值,与从大到小排列时的累积率25%对应的潮位值是不相等的,因此,将低潮序列由大到小排列,读取25%的潮位值作为乘低潮潮位也是不正确的。

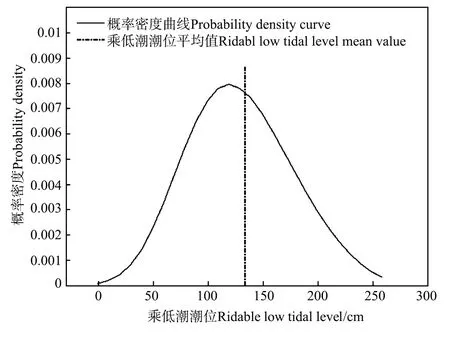
图9 胶州湾乘低潮概率密度线及其均值Fig.9 Probability density curve of ridable low tidal level and itsmean value at Jiaozhou Bay

3 结语

本文将改进最大熵分布应用于港口工程乘高(低)潮位的推算,理论曲线与实测潮位值拟合程度好,计算精度高,克服了传统手绘曲线方法读取设计潮位值的主观任意性。此外,由最大熵分布概率密度曲线,进一步阐明了乘低潮潮位的确定,应该将实测数据从小到大排列,从最大熵分布拟合曲线上,读取不同的累积率潮位作为工程设计值。

由于算例有限,最大熵分布对其他工程地点乘潮潮位的适用性有待进一步探讨。

[1] 中华人民共和国行业标准.海港水文规范(JTJ213-1998)[S].北京:人民交通出版社,1998.

[2] Ulrych T J,Thomas N B.Maximum entropy spectral analysis and autogressive decomposition[J].Rev of Geophys and Space Phys,1975,13(1):186-200.

[3] 吴克俭,孙孚.最大熵原理与海浪波高统计分析[J].海洋学报,1996,18(3):21-26.

[4] 徐福敏.最大信息熵原理在波高分布中的应用[J].河海大学学报,2000,128(1):67-71.

[5] Xu Delun,Zhang Jun,Zheng Guizhen.Maximum entropy estimation of n-year extreme wave heights[J].China Ocean Engineering,2004,18(2):307-314.

[6] 周良明,郭佩芳.最大熵原理应用于海浪波高分布的研究[J].海洋科学进展,2005,23(3):414-421.

[7] Zhang Lizhen,Xu Delun.Anew maximum entropy probability function fo r the surface elevation of nonlinear sea waves[J].China Ocean Engineering,2005,19(4):637-646.

[8] 董胜,刘伟,宁进进.台风波高重现值的泊松最大熵分布估计[J].中国造船,2009,50(4):13-21.

[9] 梁忠民,钟平安,华家鹏.水文水利计算[M].第2版.北京:中国水利水电出版社,2008,27-34.

[10] 国家海洋局第一海洋研究所港湾室《胶州湾自然环境》编写组.胶州湾自然环境[M].北京:海洋出版社,1984.