关于坐标的曲线、曲面积分向量教学方法

刘雄伟

（国防科技大学 理学院 数学与系统科学系，湖南 长沙 410073）

关于坐标的曲线、曲面积分向量教学方法

刘雄伟

（国防科技大学 理学院 数学与系统科学系，湖南 长沙 410073）

给出了积分的模型描述与计算描述形式，并给出了元素法的统一描述形式。借助于元素法给出了关于坐标的曲线、曲面积分的向量建模过程与积分模型的向量描述形式，并由向量形式给出了计算方法。

元素法；积分模型；曲线积分；曲面积分

1 积分的模型与计算描述

当一个与方向无关的待求量U是与某个范围上分布的函数f（X）相关的一个整体量，U对该范围具有可加性，即U＝ ∑ΔU，借助于“元素法”（或“微元法”），可以通过如下步骤建立积分的模型描述形式。

首先，建立适当的坐标系，在待求量U分布的范围内任取子范围，记作ΔA；然后在该范围内通过近似方法得到部分待求量ΔU，使之描述为ΔU≈f（X）ΔA，其和

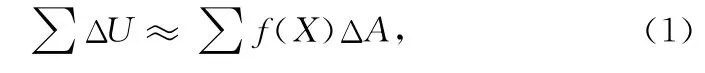
即为待求量U的整体近似值。并根据ΔA的分布范围为平行于坐标轴的线段、平面区域、立体区域、曲线或曲面，分别具有不同的积分的模型描述形式。其形式的获取通过和式（1）转换得到，如ΔA分布的范围为线（线段或曲线段，ΔA表示线长），则求和符号Σ为一个积分符号；如果为面（平面域或曲面域，ΔA表示面积）则求和符号Σ为两个积分符号；如果为体（ΔA为体积），则求和符号Σ为三个积分符号；然后将ΔA转换为dA得相应积分的模型描述形式：

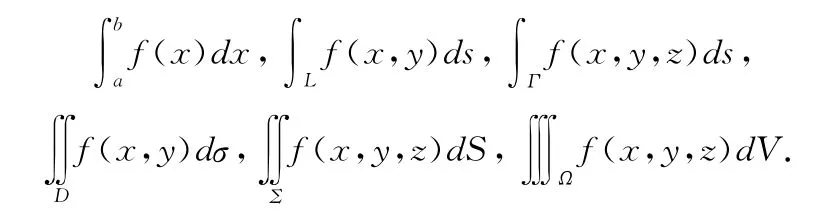
将子范围ΔA（或dA）描述成变量微元的描述形式，同时将被积函数也描述成对应变量的函数，则得到积分的计算描述形式，其中定积分的模型描述与计算描述是一致的。如设直角坐标系中的变量分别为x，y，z，则余下几种积分的直角坐标变量计算描述形式可以参见一般的高等数学教材，同样也有其他坐标系下的积分的计算描述形式或相关变量的计算描述形式，如关于弧长的平面上的曲线积分的计算描述形式可以为：

当L：y＝y（x），a≤x≤b时，有

有了积分的计算描述形式，问题就转换为获取积分变量范围得到定积分或累次积分的计算过程。以上描述形式与计算过程也适用于关于坐标的曲线积分与曲面积分。

2 关于坐标的曲线、曲面积分模型与计算

设某质点在力F＝（P（x，y），Q（x，y））的作用下，沿曲线r（t）＝（x（t），y（t）），α≤t≤β，从A（t＝α）移动到B（t＝β）。该运动过程中力所作功可通过如下过程建立其积分模型［1］。

在曲线上的任取位置P（x，y）（对应r（t）），沿着运动的方向到位置r（t＋Δt），则质点从r（t）运动到r（t＋Δt）所做的功可以近似为P位置的F＝（P（x，y），Q（x，y））沿着向量Δr＝r（t＋Δt）－r（t）所作的功，即ΔW＝F·Δr。由于Δr分布的范围为从A到B的曲线路径，所以其积分的模型描述形式为W＝∫LFdr。

由于F＝（P（x，y），Q（x，y））定义在曲线r（t）＝（x（t），y（t））上，所以力可以描述成t的表达式，即F＝（P（x（t），y（t）），Q（x（t），y（t）））；同样有

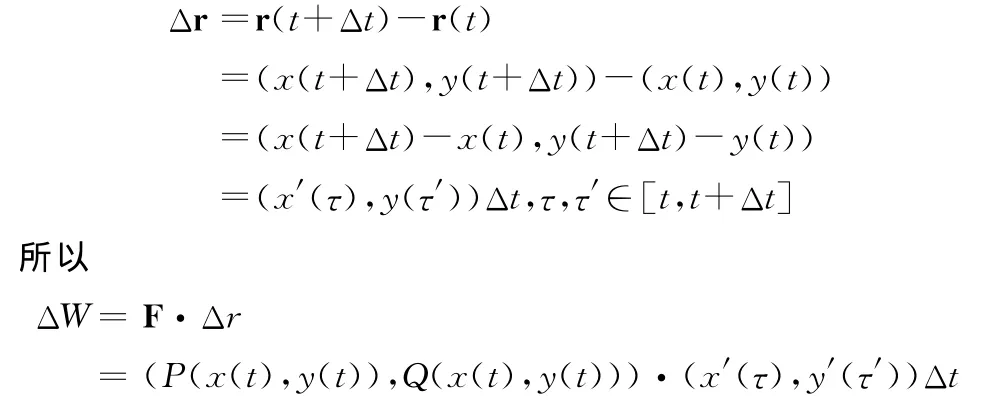
由此即可得该积分的计算描述。根据建模过程对向量的取法，可知Δt分布的范围变化是从起点t＝α变化到终点t＝β，所以

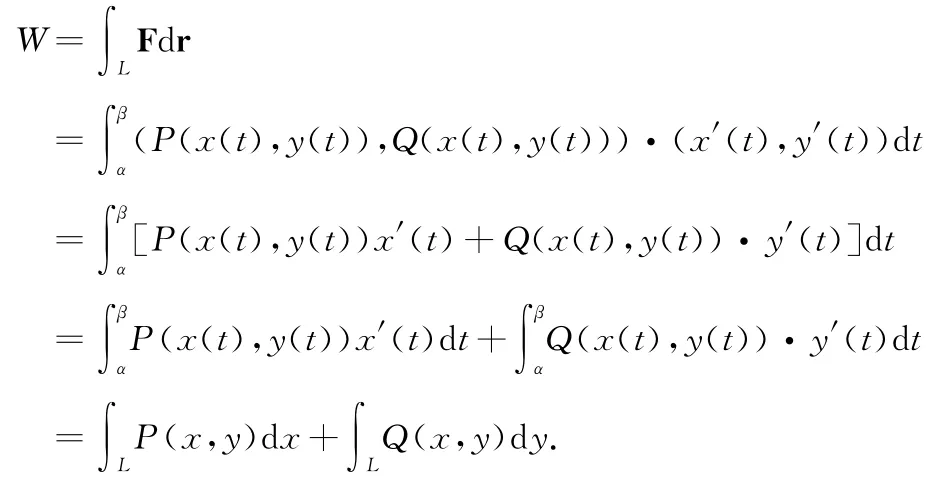
当力的坐标分量P或Q分别为零时，则得到关于y或x坐标分量的曲线积分。

同样过程也适用于流速场为v（x，y，z）＝（P（x，y，z），Q（x，y，z），R（x，y，z））穿过有向曲面Σ的流量的计算，即

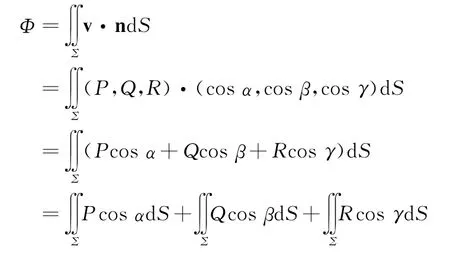
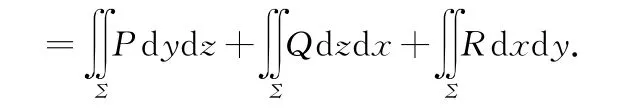
其中n为有向曲面Σ在（x，y，z）处的单位法向量。

根据曲面的方程描述形式，则可以将被积函数描述成对应坐标变量的函数描述形式而得到关于坐标的曲面积分的计算描述形式，即二重积分的计算形式。当然在转换的过程中要注意法向量的方向余弦的正负取值，决定在二重积分前面是否需要添加负号。

3 结 语

借助于元素法建模过程和积分的向量描述形式，相对于一般教材不断重复划分取近似，求和取极限的繁琐过程来说，接受更加轻松。不仅获得了关于坐标的曲线、曲面积分的模型描述形式，同时也得到了其计算方法。由于一般曲线都可以描述成不同形式的参数方程，因此参数方程的计算描述形式具有一定的通用性。而对于坐标的曲面积分对于不同的坐标变量的积分需要有对应的曲面类型，如简单的XY－型区域适合于计算关于x，y变量的曲面积分，简单的YZ－型区域适合于计算关于y，z变量的曲面积分，简单的ZX－型区域适合于计算关于z，x变量的曲面积分。在积分变量与类型不具有对应关系的时候，可以采取对曲面分片或者积分转换的方法得到合适的积分方法。

［1］朱健民，李建平.高等数学［M］，北京：高等教育出版社，2007.

Teaching Methods of Curvilinear Integral and Surface Integral for Coordinates Based on Vector

LIU Xiong－wei
（Department of Mathematics and System Science，College of Science，National University of Defense Technology，Changsha Hunan 410073，China）

This paper introduces model and calculation description form of integrals and the description of the unified form for method of element.By method of element，we give the vector modeling processes of curvilinear integral and surface integral for coordinates，also the vector description forms of these integral models.Finally we obtain the vector forms of computing methods for these integrals.

method of element；integral model；curvilinear integral；surface integral

O172.2

A

1673－0313（2011）06－0148－02

2011－09－22

刘雄伟（1974－），男，湖南安化人，讲师，主要从事高等数学教学与快速算法研究.