时滞不确定随机系统的鲁棒稳定性*

高存臣,崔红艳

(中国海洋大学数学科学学院,山东青岛266100)

时滞不确定随机系统的鲁棒稳定性*

高存臣,崔红艳

(中国海洋大学数学科学学院,山东青岛266100)

主要研究了带有时滞的不确定随机系统的均方鲁棒指数稳定性问题。根据有关线性矩阵不等式理论,结合李亚普诺夫函数法,充分利用系统的扩散项,建立了1个新的时滞相关稳定判据,使文中的时滞不确定随机系统是鲁棒均方指数稳定的。给出了具体的数值例子说明了研究结果的可行性和有效性。

随机系统;时滞;线性矩阵不等式;时滞相关指数稳定性

随着现代科学技术的发展,随机系统常带有不确定性和时间滞后。关于确定性系统的研究已经得到了全方面的关注,并得到了一些好的结果。近几年对于带有不确定项和时间滞后的系统也受到较大关注。

在过去几年里伴随着随机模型系统在科学和工程领域的重大作用,随机系统受到越来越多的关注[1-3]。特别是随机时滞系统,更加强调随机时滞系统模型的稳定性分析[4-6],这些研究又可根据时滞的类型分为2类——时滞独立系统[7-9]和时滞相关系统[4-5,10]。一般来说,对于带有较小时滞随机系统时滞独立的结果要比时滞相关保守一些。最近,对于随机时滞系统的时滞相关稳定性问题的研究得到越来越多的关注[4-5,10-12]。

本文主要探讨不确定随机时滞系统的时滞相关稳定性,通过线性矩阵不等式的方法得到了一个关于不确定随机时滞系统的时滞相关指数稳定性的判剧。这个判据不仅能够更好的构建系统的扩散项,而且具有较小的保守性。最后给出了具体的实例来说明结果的可行性和有效性。

1 预备知识

在介绍内容之前,首先做如下的说明:

(Ω,F,{Ft}t≥0,P)是1个带有自然滤子的完全概率空间;E[·]代表具有合适测度的期望算子;w(t)是定义在完全概率空间上的标准的布朗运动;如果A是一个向量或矩阵,那么AT表示它的转置;若果P是一个方阵,那么P>0(P<0)表示P是带有合适维数的对称正定(负定)矩阵;P>0(P<0)表示对称半正定(半负定)矩阵;I代表单位矩阵;用λM(·),λm(·)分别表示矩阵的最大特征值和最小特征值;|·|表示向量的欧式范数或矩阵的诱导范数;当h>0时,C([-h,0];Rn)表示定义在[-h,0]上的n维实函数φ的集合,其范数定义为0];Rn)表示F0可测且Rn)-值随机变量的集合。

考虑如下的系统

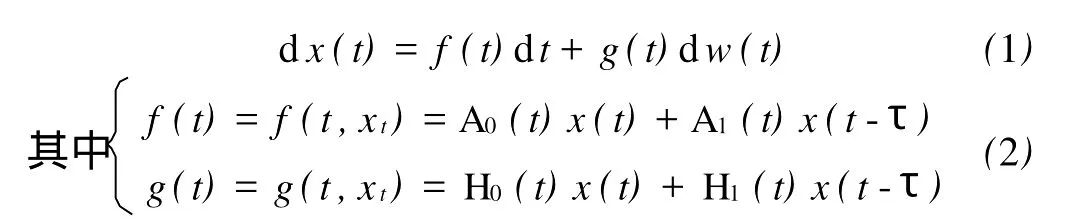
对任意的t≥0成立。

通过(2)式可以得到

其中LA,EAi,LH,EHi是勒贝格可测的未知常数矩阵且满足

如果满足(4),(5)那么存在参数不确定元素ΔAi(t),ΔHi(t),i=0,1。

定义1[8]不确定随机系统(1)是均方指数稳定的,如果存在常数λ,使得

对所有的不确定项(4)和(5)都成立。

引理1[9]令u∈Rq,v∈Rl,M∈Rq×l,对任意的常数矩阵X∈Rq×q,Y∈Rq×l,Z∈Rl×l,若成立,则下面不等式成立

引理2[10]存在任意对称正定矩阵G∈Rl×l和正数r,如果存在一个向量函数v∶[0 r]→Rl,使得积分都存在,那么下面的不等式成立

引理3[10]对任意的常数矩阵M∈Rq×l,不等式

对所有的对称正定矩阵G∈Rl×l和正数r成立。

引理4[4](Schur comp lement)对给定的常数矩阵Ω1,Ω2和Ω3满足和只要

则

2 时滞相关指数稳定性

定理1 若存在矩阵P11>0,R<0,S>0,Q≥0,W≥0,

则不确定随机系统(1)是鲁棒均方指数稳定的。这里

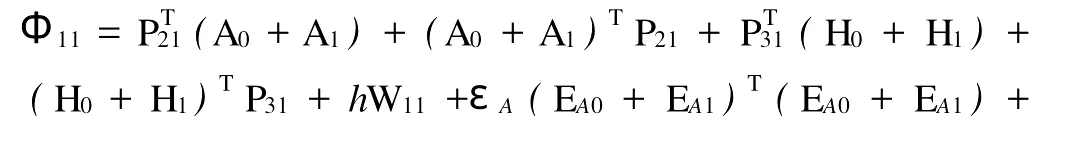
矩阵的对称部分。

证明 根据公式(1),可以得到

当t≥0时,对任意的t2≥t1≥0,有

通过(2)式和(9)式,对任意的t≥h可以得到

选择系统(9)的李亚普诺夫函数为

这里

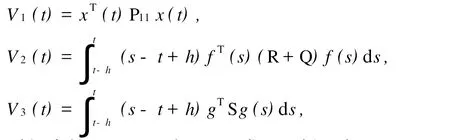
对任意的t≥h,通过It^o公式,可以得到

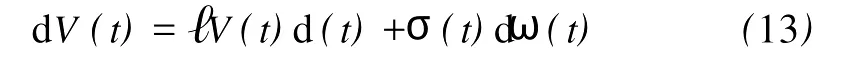
其中

令

通过等式(10)和(11),可以得到

由引理1和等式(9)～(11),有

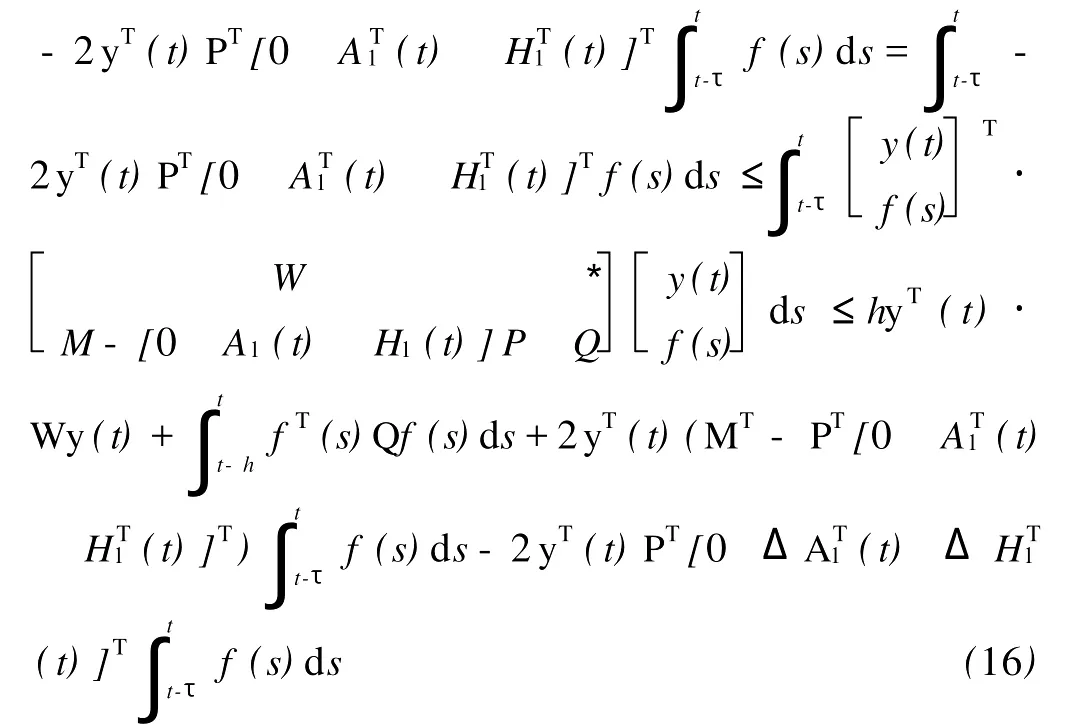
把(16)式代入(15)可以得到

这里

和

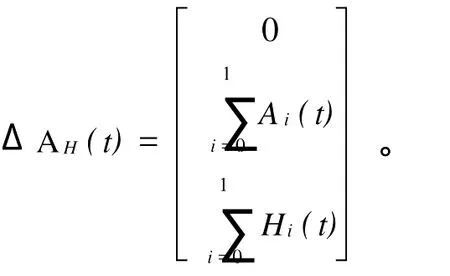
令

通过引理3,得

且

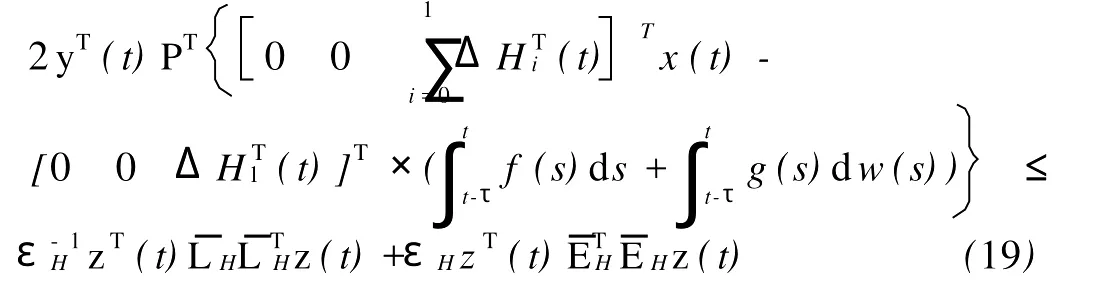
由(18)式和(19)式可得

结合不等式(15)～(20)可得

这里Γ为对称矩阵

其中

直接由引理2可得

其中

对所有的t≥h都成立。

把(21)～(23)式代入(14)式可得

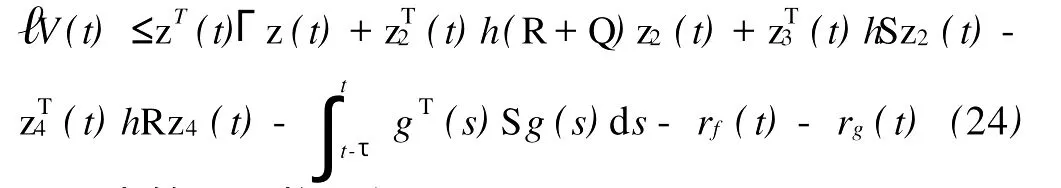
由等距同构可得

因此,在(24)式两边同时取期望可得

其中

由舒尔补引理,不等式(7)可得?Γ<0所以有

其中

由(12)式可得

令t0=h,对任意t≥t0再应用引理2,可得

通过线性增长条件(3),存在正常数C1和C2使得对所有的t≥t0下式成立

所以可得

于是系统(1)是均方指数稳定的。

3 数值例子

考虑下面的随机时滞系统

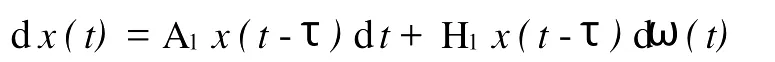
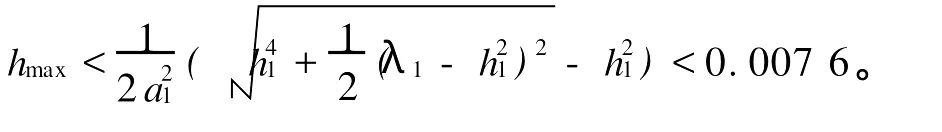
由定理1可得hmax=0.197 8,若又则λ1=1.261 5

4 小结

本文主要是通过线性矩阵不等式的方法讨论了不确定随机时滞系统指数稳定性的时滞相关判据。这里需要特别指出的是公式(10)和(11)以及4个引理对利用系统的扩散项和处理交叉项起了重要的作用,这样得到的结果保守性要小。在李亚普诺夫稳定性理论和线性矩阵不等式的基础上得到了一个新的指数相关稳定性判据。

[1] Feng Z,Liu Y.Stability analysis and stabilization synthesis of stochastic large scale systems[M].Beijing:Science Press,1995.

[2] Kolmanovskii V B,Myshkis A.Introduction to the theory and applications of functional differential equations[M].Dordrecht:Kluwer Academic Publishers,1999.

[3] Park P G.A delay-dependent stability criterion for systems with uncertain time-invariant delays[J].IEEE Transactions on Automatic Control,1999,44:876-877.

[4] Chen W H,Guan Z H,Lu X.Delay-dependent exponential stability of uncertain stochastic systems with multiple delays:An LM I app roach[J].Systems&Control Letters,2005,54:547-555.

[5] Huang L,Deng F.Robust exponential stabilization of stochastic large scale delay systems[C].[s.l.]:Proceedings of 2007 IEEE International Conference on Control and Automation,2007:107-112.

[6] Shen Y,Luo Q,Mao X.The imp roved LaSalle-type theorems for stochastic functional differential equations[J].Journal of Mathematical Analysis and Applications,2006,318:134-154.

[7] Liao X X,Mao X.Exponential stability of stochastic delay interval systems[J].Systems&Control Letters,2000,40:171-181.

[8] Mao X.Stochastic differential equations and applications[M].(2nd ed.).Chichester:Horwood Publishing,2007.

[9] Xu S,Shi P,Chu Y,et al.Robust stochastic stabilization andH1 control of uncertain neutral stochastic time-delay systems[J].Journal of Mathematical Analysis and Applications,2006,314:1-16.

[10] KGu.An integral inequality in the stability p roblem of time-delay systems[C].Sydney:Proceedings of 39th IEEE Conference on Decision and Control,2000:2805-2810.

[11] Yue D,Han Q L.Delay-dependent exponential stability of stochastic systems with time-varying delay nonlinearity,and Markovian switching[J].IEEE Transactions on Automatic Control,2005,50:217-222.

[12] Li H,Chen B,Zhou Q,et al.Delay-dependent robust stability for stochastic time-delay systems with polytopic uncertainties[J].International Journal of Robust and Nonlinear Control,2008,18:1482-1492.

Robust Stability of Uncertain Stochastic System s with Time-Delays

GAO Cun-Chen,CUIHong-Yan
(School of Mathematical Science,Ocean University of China,Qingdao 266100,China)

This paper studiesmean square robust exponentially stability of uncertain stochastic system s.With the help of linearmatrix inequality theory and Lyapunov function,and taking full advantage of diffusion in the system s,an algebraic criterion of delay-dependent stability is established for uncertain stochastic time system s.Themain results are illustrated by a numerical example.

stochastic system s;time delays;linear matrix inequality;delay-dependent exponentially stable

O231.3

A

1672-5174(2011)7/8-202-05

国家自然科学基金项目(60974025);山东省自然科学重点基金项目(Z2006G11)资助

2010-07-13;

2011-05-11

高存臣(1956-),男,教授,博导。E-mail:ccgao@ouc.edu.cn

AMS Subject Classification:93E15

责任编辑 朱宝象