数值模拟在稠油热采过程中的应用

王国库，黄志元

(1.东北石油大学;2.兰州蓝亚石油化工装备工程有限公司)

数值模拟在稠油热采过程中的应用

王国库1，黄志元2

(1.东北石油大学;2.兰州蓝亚石油化工装备工程有限公司)

对于稠油油藏来讲，其特点是粘度高、密度大、流动性差，这类油藏一般均采用热力采油方式，所以重点对稠油热采数值模拟及其计算方法进行了研究，给出稠油热采数值模拟的实现方法.

最终采收率;数值模拟;稠油热采

0 引言

近年来，随着计算机、应用数学和油藏工程学科的不断发展，油藏数值模拟方法得到不断的改进和广泛应用.通过数值模拟可以搞清油藏中流体的流动规律、驱油机理及剩余油的空间分布;研究合理的开发方案，选择最佳的开采参数，以最少的投资，最科学的开采方式而获得最高采收率及最大经济效益.经过几十年的发展 ，该技术不断成熟和完善并呈现出一些新的特点.通过数值模拟方法对油藏问题进行研究，必须建立和编制具有处理某一类特定油藏工程问题所需要的比较完善的计算机程序，其基本过程包括［1－3］:(1)建立数学模型;(2)数学模型离散化;(3)建立线性方程组;(4)线性方程组求解.

1 稠油热采数值模拟

在油藏应用中，通常只知道一些离散点的函数值.通常将有限差分网格迭加在被模拟的稠油油藏上，然后选定网格系统，用来近似连续方程中的空间导数.这样，通过离散化就把连续性方程转化为有限差分方程，使在网格点处的解可以近似的看成是此类问题的真实解［4－5］.图1是油藏模拟器开发过程中的离散化步骤的示意图.

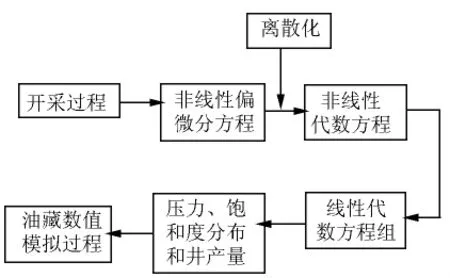
图1 油藏模拟器开发过程中离散化步骤示意图

1.1 有限差分网格的建立

对计算区域划分为均匀网格，在油藏数值模拟中，会涉及到两种类型的有限差分网格，即块中心网格和点中心网格［4］.建立网格系统的目的是把油藏分为一系列网格块，并且能把代表性的岩石性质赋给网格块.

1.2 时间差分

在油藏模拟中，问题的求解是从初始条件开始到将来时间逐渐推进模拟的过程，这里通过离散的时间步长来实现.对于时间差分，分为显式(如图2所示)和隐示差分方法(如图 3所示)［5］.而稠油热力采油方程所描述的是不稳定的渗流过程，所以方程中的各个变量都是随时间而变的.对这样的方程求解时，不能像显示格式那样逐节点依次求解，而需要联立求解，这种求解方式称为隐式格式.由于采用隐式格式时，每个时间步都要用联立方程组求解，所以与显示格式相比，它的计算量要明显增加，但是由于解的稳定性，具有显示格式所不可比拟的优势，稠油热力采油问题只能用全隐式解法.

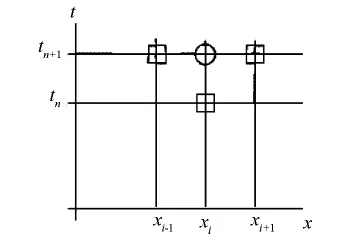
图2 显式差分方法示意图

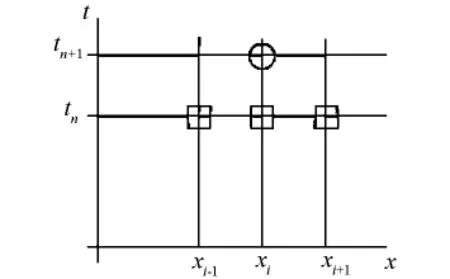
图3 隐式差分方法示意图

1.3 定解条件的假定

要得到问题所需求的工程解，微分方程必须符合初始条件和边界条件，为了得到稠油油藏模拟问题的唯一解，必须用有限差分法对初始条件和边界条件进行近似处理，并且把它们结合到油藏模拟模型中去.

1.4 线性化方法

采用 Newton－Raphson方法进行迭代求解［6］，每个内迭代步，要更新非线性方程组的系数矩阵，直到两次牛顿迭代的求解结果相差不大，则作为下一个时间步的初始值.

1.5 网格排序与求解方法

线性方程组的求解法是稠油油藏模拟中最核心的步骤之一，方程组的线性和非线性特征是由问题本身的性质以及有限差分近似的性质来决定的，即使有限差分近似法得到的是一个非线性的方程组，也可以通过线性化方法来转化成为线性形式.下面以两种常用的排序方式为例介绍排序方式引起的系数矩阵结构变化对运算时间和模拟占用的内存空间的影响.

1.5.1 自然排序

考虑一个四(ny)行六(nx)列的二维网格，如果对网格按行进行排序，使用五点差分，得到的系数矩阵为5对角结构，在产生的矩阵中，所有的非零元素都位于最上部及最下部的对角线之间，如果将带宽定义为矩阵任意行中最大元素的个数，那么，按行进行的自然排序所得到的带宽为13，这是因为按行进行的自然排序，二维问题的带宽总是等于2nx+1，如图4所示，其中nx表示任意行中网格的最大数目.

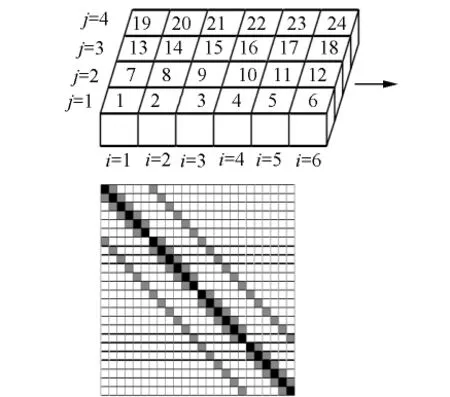
图4 按行进行的自然排列以及相应的系数矩阵

如果考虑到任意列中出现的最大网格数目总是少于出现在任意行中的最大网格数，从而按列进行网格块排序的话，得到的系数矩阵的带宽为9，即为2ny+1，如图5所示.

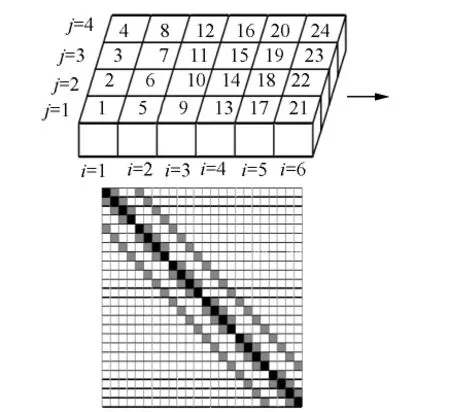
图5 按列进行的自然排列以及相应的系数矩阵

图4所需要的计算量要比图5所需要的计算量要小，因为所有的计算工作量是按照矩阵中的带宽内的元素来进行的，所以求解带宽较窄的问题比带宽较宽的问题效率高，也就是说，带宽越小，计算量越小.系数矩阵的带宽根据自然排序的方向不同是可变的，总的来说，自然排序通常都能得到带状矩阵.

1.5.2 D －4 排列

在D－4排序法中，网格块按对角线的形式进行排序，如图6所示.在该图中，阴影网格表示首先置入系数矩阵的点，空白网格则表示在此后置入的点，这种排序方法不允许相邻的两个网格块被连续地置入系数矩阵中，图6中列出了由D－4排列法产生的系数矩阵.

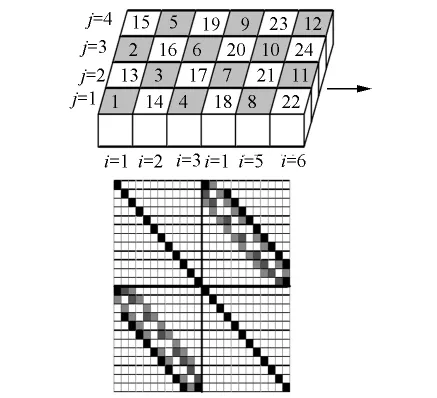
图6 D－4排列法以及相应的系数矩阵

D－4排列法产生的系数矩阵结构可以分为四个子矩阵，其中包括两个只有主对角线的子矩阵以及两个稀疏结构的子矩阵，这种D－4排列法的优点在于位于左下部子矩阵对角线上的各元素可以在消去过程的第n/2步中用来消去位于左下角的子矩阵中的元素.

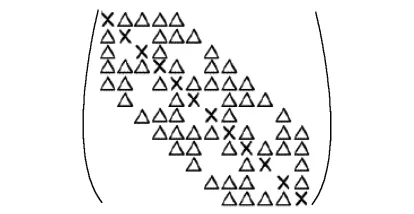
图7 由D－4排列法产生的右下侧子矩阵结构

图7表示的是经过n/2步消去之后得到的系数矩阵的结构，经过消去后的右下侧矩阵定义的方程系统通常称为简化方程组，这时，可利用直接法或者迭代法求解这个简化的方程组，完成以上两步后，可以得到一个易于回代求解的完全的三角形矩阵.

从减少计算工作量和节约存储的角度来看，D－4方法是直接法中最为优越的一种方法，当nx、ny均较大，且 ny＜nx，其预计的工作量为:W=，相应的存储量为

因此这种方法所节约的计算工作量和存储量比较显著.进而使稠油热采快速数值模拟得以实现.

2 结论

油藏数值模拟具有良好的应用前景，特别是对于稠油油藏来讲基本上都采用热力采油方式，从而在很大程度上推动了稠油热采数值模拟技术的进一步完善和发展.通过本课题的研究不仅使我们对稠油热采数值模拟的过程和计算方法有了清楚的认识，更重要的是它可以用来指导生产.

［1］布尔热，等著，杨承志，等译.热采法提高原油采收率.北京:石油工业出版社，1991.

［2］韩大匡，陈钦雷，闰存章.油藏数值模拟基础.北京:石油工业出版社，1993.

［3］Briens F L ，Wu C H，Gazdag J，et al.Compositional Reservoir Simulation in Parallel Supercomputing Environment［R］.SPE Paper 21214，1997.

［4］朱维耀，鞠岩.强化采油油藏数值模拟基本方法.北京:石油工业出版社，2002.

［5］Wette D H，Yukler M A.Petroleum origin and accumulation in basin evolution － A quantitative model［J］.AAPG Bull，1981，65(8):1387 －1396.

［6］杨耀忠，舒继武，郑纬民.基于Cluster的大型油藏数值模拟的并行计算.清华大学学报，2003，43(9):1284－1287.

Application of Numerical Simulation in Heavy Reservoir Thermal Recovery Process

Wang Guoku1，Huang Zhiyuan2
(1.Northeast Petroleum University;2.Lanzhou Lanpec Technologies Limited Compony)

The characteristics heavy reservoirs is high viscosity，density，poor liquidity and this kind of reservoir is normally made by using thermal flooding.So the targeted research of numerical simulation and calculating method of heavy reservoir thermal recovery are researched in this paper.The implementation method of numerical simulation of heavy reservoir thermal recovery is given.

Ultimate recovery rate;Numerical simulation;Heavy reservoir thermal recovery

2010－11－03

(责任编辑:黄永辉)