利用EXCEL构建大学教育基金存钱计划模型

宋 琛

（无锡广播电视大学基础部，江苏无锡 214021）

利用EXCEL构建大学教育基金存钱计划模型

宋 琛

（无锡广播电视大学基础部，江苏无锡 214021）

文中利用Excel中几个常见的内置函数，构建及验证了大学教育基金年存款计划模型，并在该模型的基础上，构建了月存月取的大学教育基金存款计划模型。另外，文中还利用EXCEL的规划求解功能，运用该模型，进行了提前存钱年限的计算及在存钱计划确定的前提下大学教育基金可供支取的学费及生活费金额的计算。

Excel财务建模；大学教育基金；规划求解

MicrosoftExcel作为企业普遍应用的办公自动化软件，具有极强的灵活性以及丰富的内置函数和各种实用工具，不仅可用于日常普通表格的制作和简单的数理统计，财务人员还能够使用它很容易地构建出复杂的财务模型。文中即利用Excel中几个常见的内置函数，构建及验证了大学教育基金存钱计划模型，并利用该模型进行了其它相关问题的求解。

一、问题的提出

有这样一个问题：在你的孩子刚刚出生的时候，你开始为她的大学教育基金存钱了。如果她将会正好在她18岁生日那天开始她的大学生活，并且在她大学生活开始的前三年，你可以继续向她的大学教育基金中存入金额，直至她大学最后一年开始，那时，最后一笔学费要付出了。预期她大学四年的大学学费将达到每年15000元，且教育基金能获得每年5%的利息。那么，你每年至少要存入多少钱？

为了回答这个问题，我们利用Excel构建了如表1所示的模型。

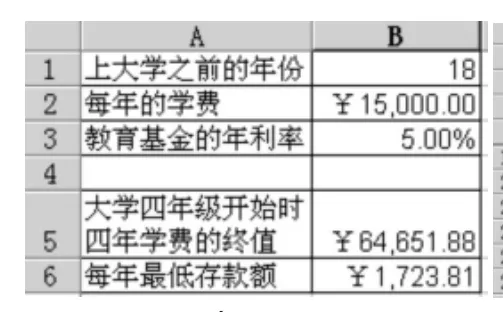
表1

表2

二、几点说明

关于该模型，有以下几点说明：

1、表1中大学四年级开始时四年学费的终值，即B5单元格的计算公式为：B5＝FV（B3,4,-B2），其中FV（）函数的功能和语法结构如下：

·FV（）函数

语法：FV（rate，nper，pmt，pv，type）其中 rate为各期利率，nper为总投资期，pmt是各期所获得的金额，在整个投资期内不变，pv是从该项投资开始计算时已经入账的款项或一系列为了付款当前值的累积和。如果忽略则pv＝0，type是逻辑值0或者1，用以指定付款时间在期初还是期末，如果为1，付款在期初，如果为0或忽略，付款在期末。

通过本单元格的计算，我们得知了一共要向大学教育基金存入的四年大学学费的总金额在大学四年级开始时的终值为64651.88元。

2、表1中每年最低存款额，即单元格B6的计算公式为：B6＝-PMT（B3,B1+3,,B5,1），其中PMT（）函数的功能和语法结构如下：

·PMT（）函数

功能：返回在固定利率下，投资或贷款的等额分期偿还额。

语法：PMT（rate，nper，pv，fv，type）其中 rate、nper、pv、type等各项参数同FV（）函数，而参数fv是未来值，或在最后一次付款后可以获得的现金余额。

此单元格即计算出了在5%的存款利率条件下，在长达21年的时间内，要获得64651.88元的最终存款总额，则必须每年至少存入教育基金账户的金额为1723.81元。

3、关于此表结果正确性的检验，我们只需构建一张教育基金收支一览表即可。如表2所示。

4、如果年存款计划改为月存款，则只需修改一下该模型，即可获得想要的结果。

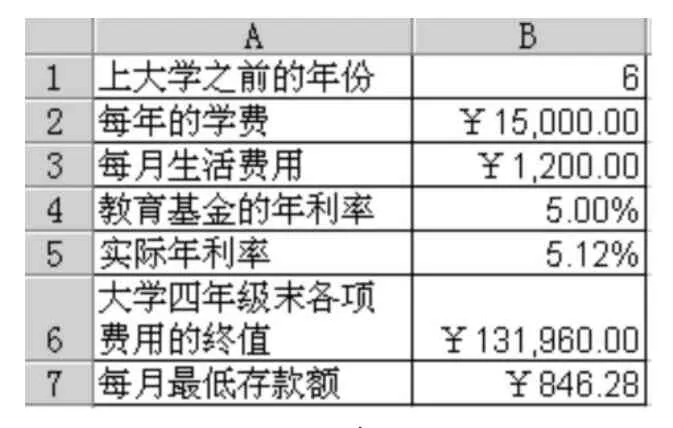
表3

比如有这样一个问题：你的小孩刚升入中学，预计还有6年的时间，将开始她的大学生活。预计她大学4年每年学费为15000元（按年支付），而生活费为每月1200元（按月支取），因此，你现在开始为她的大学费用存钱了。假设你可以持续向她的大学教育基金中存入金额，直至她大学最后一月。那么，在5%的利率条件下，你每月向基金账户存入的金额至少应为多少？

解答该问题的模型如表3所示，其中单元格B5的计算公式为：B5＝（1+B4/12）^12-1，因为已知的是基于期间为月的名义年利率，故B5单元格计算了实际年利率为5.12%。B6＝FV（B5,4,-B2,,1）+FV（B4/12,4*12,-B3,,1），计算了大学4年的学费及各月生活费，到小孩大学毕业前最后一个月初去提取生活费时的总费用的终值为131960.00元。B7＝-PMT（B4/12,（B1+4）*12,,B6,1），从而计算出每月应存入的金额为846.28元。证明从略。

三、模型的其他应用

运用以上讨论的大学教育基金存钱计划模型，我们除了可以用来进行每年或每月存钱金额多少的计算以外，还可以利用EXCEL强大的计算功能，进行其他我们感兴趣的问题的求解。

（1）计划存钱年限的计算

同上例，预计小孩大学4年每年学费为16000元（按年支付），而生活费为每月1000元（按月支取），而你计划每月存款为1000元，那么在5%的利率条件下，你必须提前多久开始你的教育基金存钱计划？

为了解决这个问题，我们利用上述讨论的教育基金存钱计划模型，利用EXCEL的规划求解功能，来完成相应计算。如图1所示，将B7单元格设为目标单元格，并且设定目标单元格的值为1000元，将B1单元格，也就是上大学之前的年份作为可变单元格，点击求解按钮，EXCEL就会进行迭代计算，从而给出相应的计算结果为4.4207年，如表4所示。

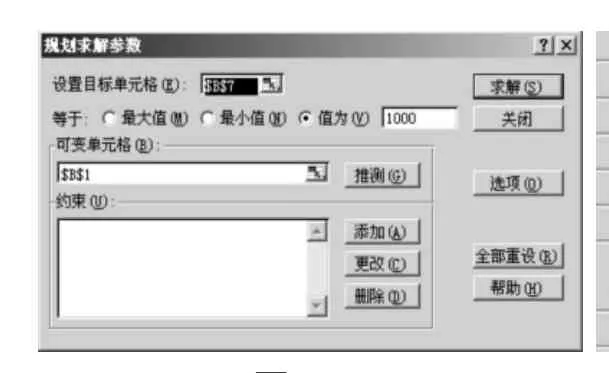
图1

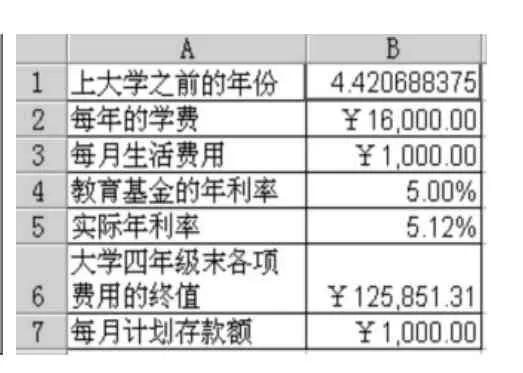
表4

（2）限额支取费用的计算

我们同样可以利用EXCEL的规划求解功能，利用该模型，在有了存款计划后，即在提前开始存钱的年限及每月存钱金额已确定的情况下，来预测可供小孩今后选择学费在什么范围内的学校，或者预测在学费固定的情况下，每个月供小孩花费的生活费为多少。具体数据如表5、表6所示。

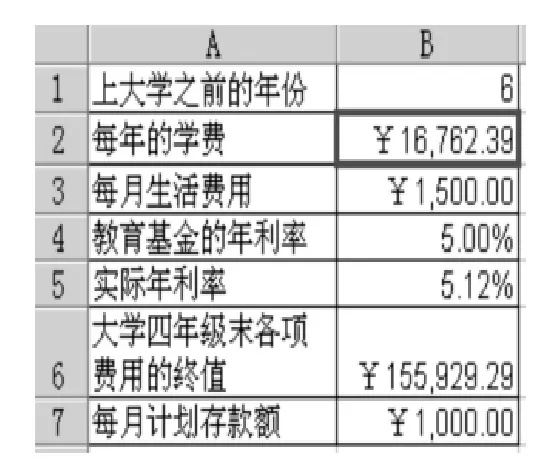
表5

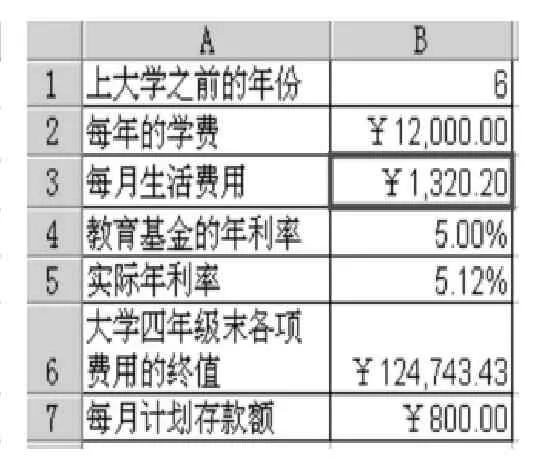
表6

四、结语

由上述讨论可以看出，我们可以利用EXCEL强大的计算功能和丰富的内置函数，构建一大学教育基金存钱计划模型。利用该模型，我们可以计算出各种条件下每年或每月应向教育基金存入的金额的多少。还可以利用EXCEL的规划求解功能，运用该模型，进行提前存钱年限的计算及在存钱计划确定的前提下大学教育基金可供支取的学费及生活费金额的计算。这在大家都十分注重教育投资的今天是具有一定的现实意义的。

［1］小特洛伊.A.阿代尔.EXCEL在财务管理中的应用［M］.中国人民大学出版社,75-82.

［2］国际财务管理师资格考试中国指导教材编写组.财务管理［M］中国财政经济出版社,2005.

F830.48 < class="emphasis_bold">［文章标识码］ A

A

1671-5136（2011） 03-0077-02

2011-09-07

宋琛（1972—），女，江苏无锡人，无锡广播电视大学基础部讲师、硕士。研究方向：EXCEL在财务管理中的应用、物流管理等。功能：基于固定利率及等额分期付款方式，返回某项投资的未来值。