一类永磁同步电动机的TSM控制器设计

马新，平静水

（淮南师范学院 数学与计算科学系，安徽 淮南 232038）

一类永磁同步电动机的TSM控制器设计

马新，平静水

（淮南师范学院 数学与计算科学系，安徽 淮南 232038）

基于永磁同步电动机精确的数学模型，针对永磁同步电动机绕组相电流和转速强耦合特性,依据中继切换控制机制和有限时间收敛的终端滑动模态控制机制，考虑了永磁同步电动机的有限时间跟踪问题。给出了其终端滑模控制器的设计方案。在所设计的控制作用下，闭环系统将在有限时间内达到平衡状态。并且保证了闭环系统所有信号的有界性和平衡点的全局稳定性，以及系统在有限时间内精确地跟踪给定的参考信号。最后对一具体的永磁同步电动机模型进行了数值仿真，仿真结果表明在所设计的终端滑模控制器作用下，系统的跟踪误差在有限时间内达到零，验证了所提算法的正确有效性。

终端滑动模态；永磁同步电动机；中继切换控制

1 引言

永磁同步电动机(PMSM)是工厂自动化，生产自动化不可缺少的基本技术装备。不论在有功消耗，还是无功耗损方面都优于大量使用的交流电动机，可以说现代永磁同步电动机是一种节能降耗的机械产品。因此，永磁同步电动机系统的快速性、稳定性和鲁棒性的好坏成为决定电动机性能优劣的重要指标。

永磁同步电动机系统是一个非线性多变量耦合系统，这样传统的线性控制方案已经不能满足人们对控制精确度的要求。随着现代控制理论的发展，永磁同步电动机的控制技术也在不断地更新，人们开始使用非线性控制系统的方法来设计新的控制方案，这方面的研究成果很多，如非线性解耦控制[1]、人工神经网络控制、模糊控制[2-6]、变结构控制[7]等新的控制策略。文献[6]在滑模控制策略中引入模糊控制算法，很好地解决了抖振问题，对参数变化和负载扰动具有很好的鲁棒性。

尽管永磁同步电动机系统的稳定性问题已经有很多研究，但跟踪控制问题却很少有人研究，文献[8]中采用了Backstepping方法对永磁同步电动机的数学模型进行线性化处理，设计电机全状态反馈控制器，实现永磁同步电动机的线性动态解耦控制，其滤波跟踪误差迅速以指数特性收敛到零，达到较好的位置伺服控制特性。有限时间收敛控制器是一种快速控制机制[9-11]，当系统状态在有限时间内收敛时，它的性能达到理想点。对于强耦合高阶系统，当某些状态在有限时间内达到零时，将对其它状态不再有影响。文献[12]中将该方法应用于机器人模型，取得了很好的控制效果。目前，将有限时间收敛控制方法应用于永磁同步电动机控制系统的研究结果并不多见。本文通过引入TSM有限时间收敛控制机制，对永磁同步电动机设计了一个分段全局跟踪控制器。该控制器保证了永磁同步电动机控制系统的跟踪误差以及控制信号在有限时间内收敛到零，并且永远保持为零。仿真结果说明该控制策略的有效性。

2 系统描述

为了研究方便，做如下假设：①磁路不饱和，磁滞及涡流的影响忽略不计；②空间磁势及磁通呈正弦分布；③永磁同步电动机的交、直轴电感相等。在同步旋转坐标 下，永磁同步电动机的数学模型可以描述为：

其中φ和ω分别表示电动机的机械角度和角速度，（iq，id）和（uq，ud）为固定的定子框架上分别表示定子的电流和电压，该电动机的参数是定子电阻R和交、直轴等效电感L，转子的转动惯量J，粘滞摩擦系数B和电动机极对数P，永磁磁通ψ，负载转距TL，除TL外所有参数均为正数，假设φr和ω*分别表示理想的电动机的机械角度和角速度。

控制任务是：通过调节定子的电压，使得电动机的机械角度φ和角速度ω分别在有限时间内达到理想的机械角度φr和角速度ω*。

为方便计，定义跟踪误差：

这里v1，v2是一种广义的电压输入信号，对于系统（4），原控制任务演化为设计控制信号v1，v2，使得跟踪误差x1e，x2e在有限时间内达到零，实现完全跟踪。

3 控制器设计

首先考虑系统（4）的最后一个方程，并取广义电压输入信号v2为

则x4e到达零的时间T0为

由此验证了x4e在某一有限时间T0内收敛到零，

于是，当 t＞T0时，由（4）可得

下面引入一个坐标变换使得系统（9）化为可控标准形，使之在新坐标系下更便于设计TSM控制器，定义非奇异的坐标变换

其中 y1，y2，y3相应于广义跟踪误差， 于是系统（9）可化为

下面设计 v1，使得 yi（i=1，2，3）在有限时间内收敛到零，取TSM流行[10]为：

其中 β1，β2为正常数，pi＞qi（i=1，2）均为正奇数。

取

其中 K＞0，由文献[10]可知，存在有限时间 T（T＞T0），当 t＞T 时，y1，y2，y3及 v1都收敛到零， 并且永远保持为零，由文献[9]，当参数 pi＞qi（i=1，2）满足条件（k=0，1，n=3）时，在 y1，y2，y3及 v1趋向于零的过程中，控制量v1是有界的。

当 y1，y2，y3收敛到零时，由可逆变换（10）可知,x1e，x2e，x3e在有限时间 T 之后变为零,于是由（5）式得到v2也在有限时间内到达零。由x1e，x2e的定义可知 φ（t），ω（t）在有限时间内分别完全跟踪理想状态 φr（t），ω*（t）。

由（5）式可求得定子的电压为：

当t＞T时，由上述分析易知电压uq，ud为有界的信号。

定理：对于给定的永磁同步电动机系统（1），设φr和ω*分别为理想的机械角度和角速度，广义电压输入信号 v1，v2分别由（13）和（6）给出，TSM 切换面由（12）式给出，则在某一有限时间T之后，电动机的机械角度φ和角速度ω将精确地跟踪到理想的机械角度φr和角速度ω*，跟踪误差达到零并且永远保持为零，且在整个跟踪过程中，系统的所有信号是有界的。

永磁同步电动机系统（1）的TSM控制器的设计步骤如下：

1.取控制律 v1=0，v2如（6）式所示，则 x4e在有限时间T0内收敛到零.

2.在 T0时间之后，取 v1如（13）所示，则 y1，y2，y3在有限时间T内收敛到零， 即x1e，x2e，x3e在有限时间T内收敛到零。且控制量v1，v2在有限时间内收敛到零并在整个收敛过程中是有界的。

4 仿真研究

对于给定的永磁同步电动机系统（1），设其参数设置如下：

定子的电阻R=0.18Ω，等效电感L=0.0699H，永磁磁通 ψ=0.175Wb，转动惯量 J=0.006kg·m2，粘滞摩擦系数B=0.01kg/s，电动机极对数P=4，负载转距 TL=2sint（N·m）。TSM 参数取为：q=q1=q2=3，p=p1=p2=5，β=β1=β2=5，k=5，初始值为：x1e（0）=2，x2e（0）=1，x3e（0）=1，x4e（0）=1。

理想的机械角度 φr和角速度 ω*为：φr=sint（rad），ω*=cost（rad/s）。

图1（a）—（d）为跟踪误差和控制律随时间的变化曲线。图2（a）—（d）为定子电压以及实际机械角度和角速度跟踪理想的机械角度和角速度随时间的变化曲线。

图1 跟踪误差和控制律随时间的变化曲线

由图1（a）可知跟踪误差x4e在大约0.5秒的时间收敛到零；图 1（b）和（c）表明跟踪误差x1e，x2e，x3e及控制律 在大约6.5秒的时间收敛到零；图1（d）表明控制律v1在6.5秒以后达到零并永远保持为零。

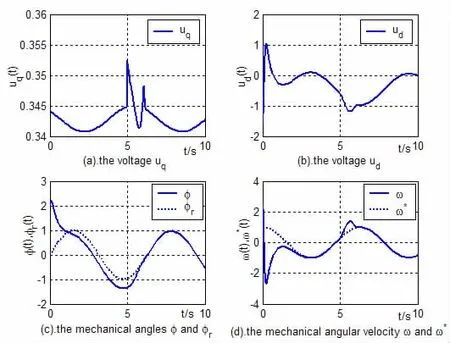
图2 电压及机械的角度和角速度随时间的变化曲线

由图2（a）-（b）可以看出电压在整个控制过程中始终是有界的.由图 2（c）-（d）可以看出实际机械的角度φ和角速度ω在有限时间（6.5秒）以后可以实现对理想的机械角度φr和角速度ω*的完全跟踪。

5 结论

本文将递推TSM有限时间收敛的控制方法应用于永磁同步电动机系统，充分利用了有限时间跟踪控制方法的分析简单，动态响应快，应用广泛等优势，保证了系统状态在有限时间内达到完全跟踪的目的，仿真结果充分显示了该控制策略的有效性。

[1]孙晓东等.一种永磁同步电机解耦控制的新方法[J].微电机，2010，43（1）：61-65

[2]SINGH B，REDDY A H N，MURTHY S S.Hybrid fuzzy logic proportional plus conventional integral-derivative controller for permanent magnet brushless D C motor[C].In：Proceedings on Industrial Technology，2000：185-191

[3]GHANDAKLY A A OWED M R.Design of an adaptive speed controller for D C brushless motors[C].In：Proceedings on Industry Applications Conference，1995： 1626-1663

[4]PRTER A.Artificial-intelligence-based electrical machines and drives application of fuzzy，neural，fuzzy -neural，and genetic -algorithm -based techniques [M]. Oxford New York：Oxford University Press，1999

[5]JOHANSON J P.RAHMAN K M，EHSANI M.Application of a clustering adaptive fuzzy logic controllerin a brushless D C drive[C].In：Proceedings on Industrial Electronics，Control and Instrumentation，1997：1001-1005

[6]黄石维，周国荣.永磁同步电机的模糊滑模控制[J].机械工程与自动化，2010，（1）：150-154

[7]王家军，许镇琳，王豪，孟明.基于逆变死区特性的永磁同步电动机系统的修整变结构控制[J].中国电机工程学报，2003，（4）：148-152

[8]李三东，沈艳霞，纪志成.永磁同步电机位置伺服控制器及其Beckstepping设计[J].电机与控制学报，2004，8（4）：353-356

[9]YU X Y，Man Z H，Model reference adaptive control systems with terminal sliding modes[J].InternationalJournalofControl，1996，64 （6）：1165-1176

[10]WU Y Q，YU X Y，Man Z H.Terminal sliding mode control design for uncertain dynamic systems[J].Systems&Control Letters，1998，34（5）：281-287

[11]郑雪梅，冯勇，鲍晟.非匹配不确定系统的终端滑模分解控制[J].控制理论与应用，2004，21（4）：617-622

[12]WU Y Q，ZONG G D.Relay switching controller with finite time tracking for rigid robotic manipulators[J].Acta Automatic Sinica.2005，31（3）：412-418

Terminal sliding mode controller design for a class of permanent-magnet synchronous motor

MA Xin，PING Jing-shui

The precise position control of a permanent magnet synchronous motor is a more complicated problem due to the multi-input multi-output nature of the motor and the significant nonlinear coupling among its phase winding currents and the rotor velocity.Based on the exact model of the PMSM，finite time tracking controller design is considered using the relay switching control mechanism and the terminal sliding mode control scheme.Under the designed controller，the system state of the closed-loop system will reach the equilibrium in a finite time.Moreover，the boundedness of all the signals of the closed-loop system and the global stability of equilibrium point are guaranteed and the system states accurately track the states of the reference signal in a finite time.Finally，a numerical simulation was given for a concrete PMSM model.The simulation results show that the system tracking error can become zero in a finite time under the designed terminal sliding mode controller，and numerical simulations validate the efficiency of the control scheme.

terminal sliding mode；permanent-magnet synchronous motor；relay switching control

O231

A

1009-9530（2011）04-0076-04

2011-04-22

安徽省高等学校省级自然科学研究项目（KJ2011Z344）；淮南师范学院青年科研项目（2010QNL02）

马新（1980-），女，山东高密人，淮南师范学院数学与计算科学系助教，硕士研究生，研究方向：非线性控制与变结构控制。平静水(1964-)，男，安徽凤台人，淮南师范学院数学与计算科学系副教授，主要研究模糊数学的应用。