一类积分微分方程周期解的稳定性

崔冬玲

（淮南师范学院 数学与计算科学系，安徽 淮南 232001）

一类积分微分方程周期解的稳定性

崔冬玲

（淮南师范学院 数学与计算科学系，安徽 淮南 232001）

利用泛函分析的技巧讨论了一类对具有连续时滞非线性积分微分方程周期解的稳定性。

非线性积分微分方程；周期解；稳定性

1 引理及假设

考虑如下微分方程

引理 设 X（t）是（1）的基本解方阵，则有

解的右上导数，可得

两边同时取从s到t的积分有

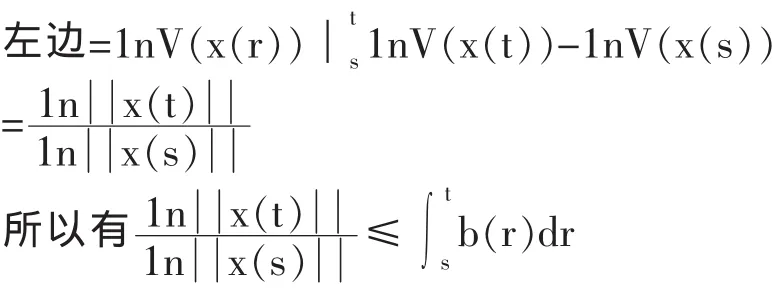
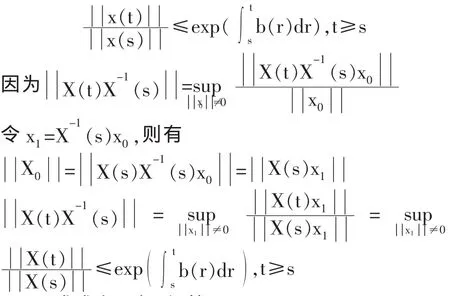
即（2）式成立，引理证毕。

定义：方程（3）的零解是一致稳定的，如果对于每一个 ε＞0和任何的 t0≥0，存在着正数 δ=δ（ε（与 t0无关）使得当时，就有成立。

考虑如下的积分微分方程）

（A5）存在着常数 K＞1 使得当 t∈R 时有

其中 b（t），b1（t），b0（t）分别由（A1），（A3），（A4）中给定。

2 主要结果及其证明

所以

设 B（t）是 b（t）的一个原函数，则有

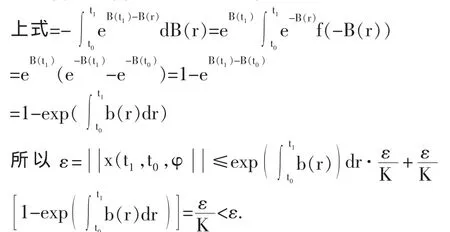
这就发生了矛盾，这个矛盾说明 x（t，t0，φ ＜ε（当 t＞t0时）。 因为 δ 与 t0无关，故（3）的零解是一致稳定的。

[1]黄启昌.具无限时滞的泛函微分方程的周期解的存在性[J].中国科学，1984，（10）：882-889

[2]王全义.微分积分方程的周期解的存在唯一性[J].华侨大学学报，2001，22（1）：1-5

[3]Zhou Z.F.，Periodic Solution for a class of higher dimensional retarded functional differential equations[J]．Journal of Math.（PRC），2002，22（4）：423-430（in china）

[4]郑祖庥.滞量与周期解的存在性[J].安徽大学学报，1981，5（2）：22-28

[5]李森林，温立志.泛函微分方程[M].长沙：湖南科学技术出版社，1987

The stability of periodic solutions of a kind of integral differential equation

The stability of periodic solutions of a kind of nonlinear integral-differential equations with continuous delay is discussed in this paper mainly by the method of functional analysis.

nonlinear integral-differential equation；periodic solution；stability

CUI Dong-ling

O175.6

A

1009-9530（2011）04-0063-02

2011-03-04

安徽省高校省级自然科学研究项目（KJ2010B445）

崔冬玲（1979-），女，黑龙江宝清人，淮南师范学院数学与计算科学系讲师，研究方向：泛函微分方程。