遗传投影寻踪插值模型在纸浆质量评价中的应用
熊智新 胡慕伊 陈朝霞 胡 明
(南京林业大学江苏省制浆造纸科学与技术重点实验室,江苏南京,210037)
纸浆质量综合评价就是根据造纸工业产品标准等级评价指标,对从不同侧面获得的纸浆性能数据进行总的评价,从而全面地分析被评对象的质量状况,为开发利用新的纸浆纤维原料,改进制浆工艺,或是定向培育纸浆材林提供科学的决策依据。但是目前国内外尚无统一的纸浆质量评价模型。不同工艺条件下得到的纸浆指标值不同,而且分级范围比较广,纸浆分级界限具有一定模糊性,因此文献[1-2]提出了评估纸浆质量的模糊数学模型,实现了纸浆质量的综合评估。但是用模糊数学进行综合评价,需要根据评价等级标准设计若干个隶属函数,而这种设计还没有系统的方法,其结果的可靠性和准确性依赖于合理选取指标、指标的权重分配和综合评价的合成算子等。因此,总的来讲,模糊综合评判是一种基于主观信息的综合评价方法[3]。
纸浆质量评价实际是一个多属性决策问题,这些属性之间存在着复杂的关系,在统计学中称之为高维问题,从而增加了评价的难度。投影寻踪(Projection Pursuit,简称PP)是由美国科学家Kruskal提出的一种用以分析和处理高维观测数据,尤其是非线性、非正态高维数据的新兴统计方法,是统计学、应用数学和计算机技术的交叉学科,已被用于洪水灾情、环境质量、农业资源等领域进行分级综合评价[4-6]。本研究将利用基于遗传算法[7](Genetic Algorithm,简称GA)寻优的投影寻踪方法,把纸浆质量多指标评价问题转化为单一的投影指标问题,根据最佳投影值与其对应等级之间所呈现的关系建立数学模型——遗传投影寻踪插值模型(Genetic Projection Pursuit Interpolation Model,简称GPPIM),并对不同树种在相同工艺条件下的高得率浆的质量进行综合评价。
1 建立纸浆质量综合评价等级标准
影响纸浆质量的因素有很多,人工评价制浆性能和纸浆质量涉及的考核指标通常有纸浆得率、电耗、打浆度、松厚度、平滑度、粗糙度、抗张指数、撕裂指数、耐折度、白度和不透明度等。为了使综合评价体系具有针对性和实用性,一般应该按浆种生产的目标纸产品来确定各项评价指标。本研究以薄页文化用纸类对浆的质量要求为例讨论,相应的主要质量指标有:松厚度、抗张指数、撕裂指数、耐破指数及白度。由于不同制浆工艺条件所得纸浆性能不同,因此往往考虑在相同工艺条件下进行纸浆指标等级标准划分。本研究确定的纸浆性能评价分级标准采用文献[2]的结果,具体数据见表1。
2 GPPIM的计算原理与步骤
投影寻踪是一种直接由样本数据驱动的探索性数据分析方法,其建模基本思想是采用投影指标函数(目标函数)来衡量投影暴露某种结构特征可能性的大小,寻找出使投影指标函数达到最优(即最能反映高维数据结构或特征)的投影方向,把高维数据投影到低维子空间,然后根据样本数据在该方向投影值对样本集进行相应的分析[8],达到研究分析高维数据的目的。其中,投影指标函数的构造及其优化问题是应用投影寻踪解决实际问题的关键。本研究采用现代优化算法中广泛使用的具有全局寻优和并行计算能力的遗传算法处理该问题,建立纸浆质量的综合评价插值型投影寻踪模型GPPIM,其主要计算包括:
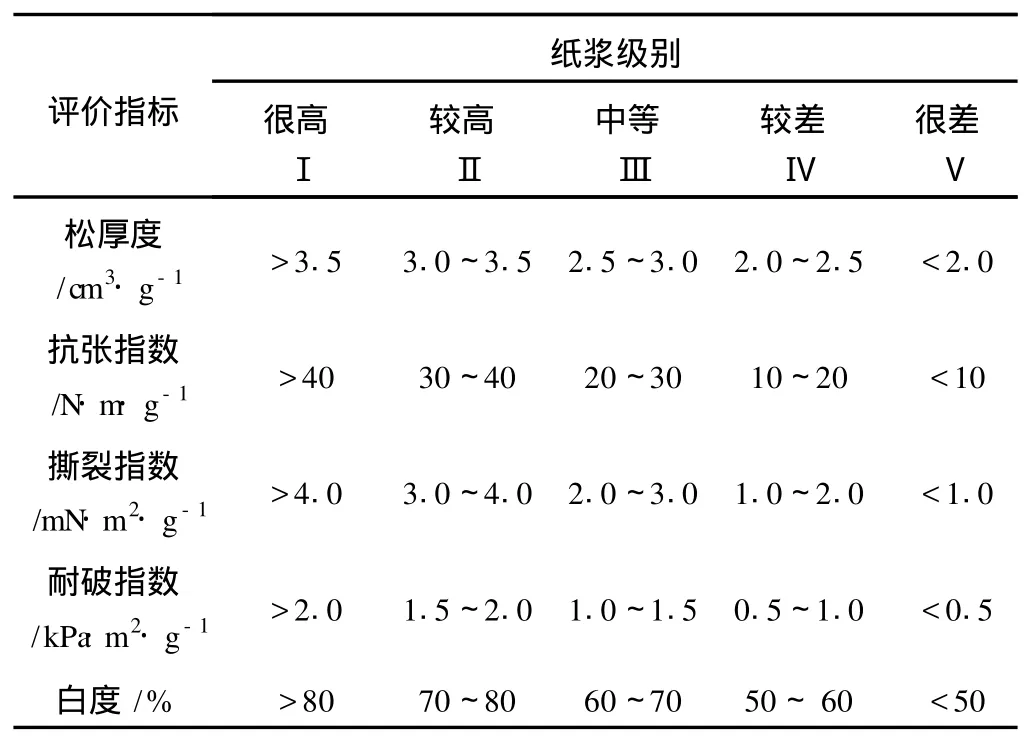
表1 纸浆质量单指标等级划分表
(1)建立投影数据 根据纸浆质量等级评价标准产生用于纸浆质量等级评价的原始数据,它包括纸浆指标及对应质量等级y(i),其中,i=1,2…,n;j=i=1,2…,p;n,p分别为样本的个数和纸浆质量评价指标数,则为第i个纸浆样本的第j个指标值。纸浆质量越好,对应等级就越高,设纸浆质量最高评价等级为1级(很高),最低评价等级为N级(很差),则y(i)∈[1,N]。为消除各评价指标的量纲效应,使模型具有一般性,对进行归一化处理为:
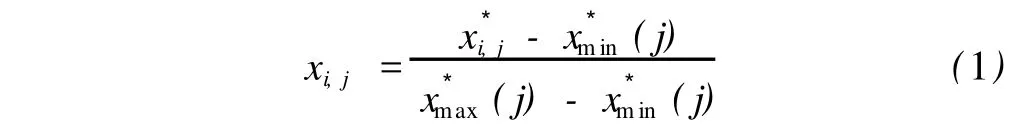
(2)计算投影值 设投影方向为a=(a1,a2,…,ap),PP方法就是把p维数据{xi,j|j=1,2,…,p}综合成以a为投影方向的一维投影值z(i):

(3)构造投影指标函数在综合投影值时,要求投影值z(i)应尽可能大地提取xi,j中的变异信息,并且能保证投影值对评价对象具有很好的解释性。即z(i)的标准差Sz尽可能大,同时要求z(i)与y(i)的相关系数Rzy的绝对值|Rzy|也尽可能大[6]。因此,投影指标函数Q(a)可构造为:
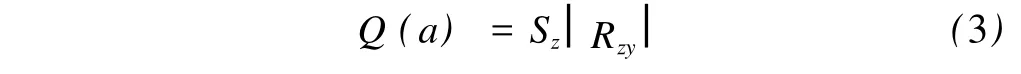
其中:
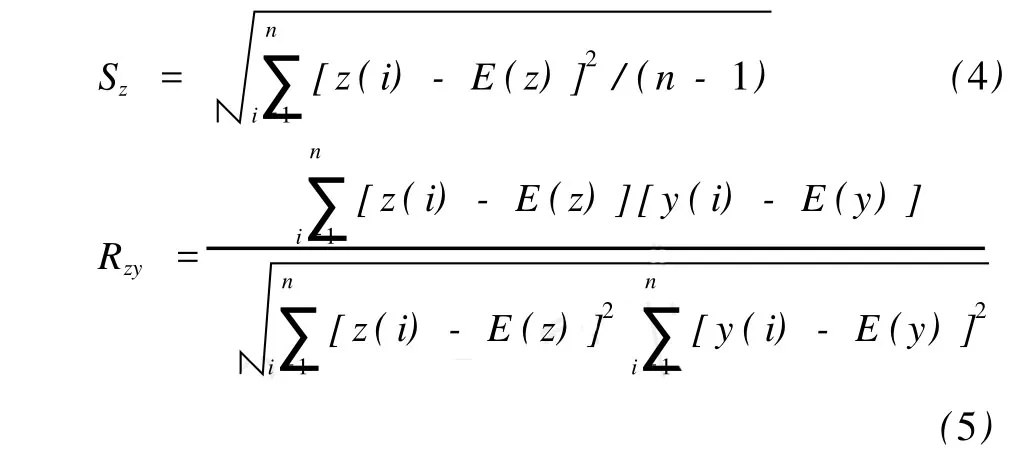
式中:E(z)和E(y)分别为序列{z(i)|i=1,2,…,n}和{y(i)|i=1,2…,n}的平均值。
(4)用遗传算法优化投影方向 当设定经验等级及其评价指标的样本数据后,投影指标函数Q(a)只与投影方向a有关,不同的投影方向反映不同的数据结构特征。可通过求解投影指标函数最大值问题来估计最佳投影方向,即:

这是一个以a=(a1,a2,…ap)为优化变量的非线性优化问题,采用传统投影寻踪技术计算复杂、编程实现困难,在一定程度上限制了其应用[6]。模拟生物优胜劣汰规则与群体内部染色体信息交换机制的遗传算法是一种通用的全局优化方法,用它来求解上述问题则较为简便。遗传算法的具体算法可参见文献[6-7]。
(5)建立纸浆质量评价的数学模型 把由步骤(4)求得的最佳投影方向a*代入式(2),可求得各样本点的最佳投影值z*(i),反映各样本的综合质量特征。根据z*(i)与y(i)的散点图即可建立纸浆质量评价的投影寻踪插值模型。
3 实例计算
为了说明GPPIM用于纸浆质量综合评价的可行性,本研究直接采用文献[2]的制浆实验数据,其中5个树种纸浆均在相同工艺条件下采用P-RC APMP方法制得,其性能指标见表2。在表1所示的纸浆质量5个评价等级取值范围内分别均匀随机产生共5×100个指标样本,与对应的5个等级y(i)一起组成样本数据,并对按式(1)进行归一化处理为:
xi,j(i=1,2,…,500;j=1,2,…,5),
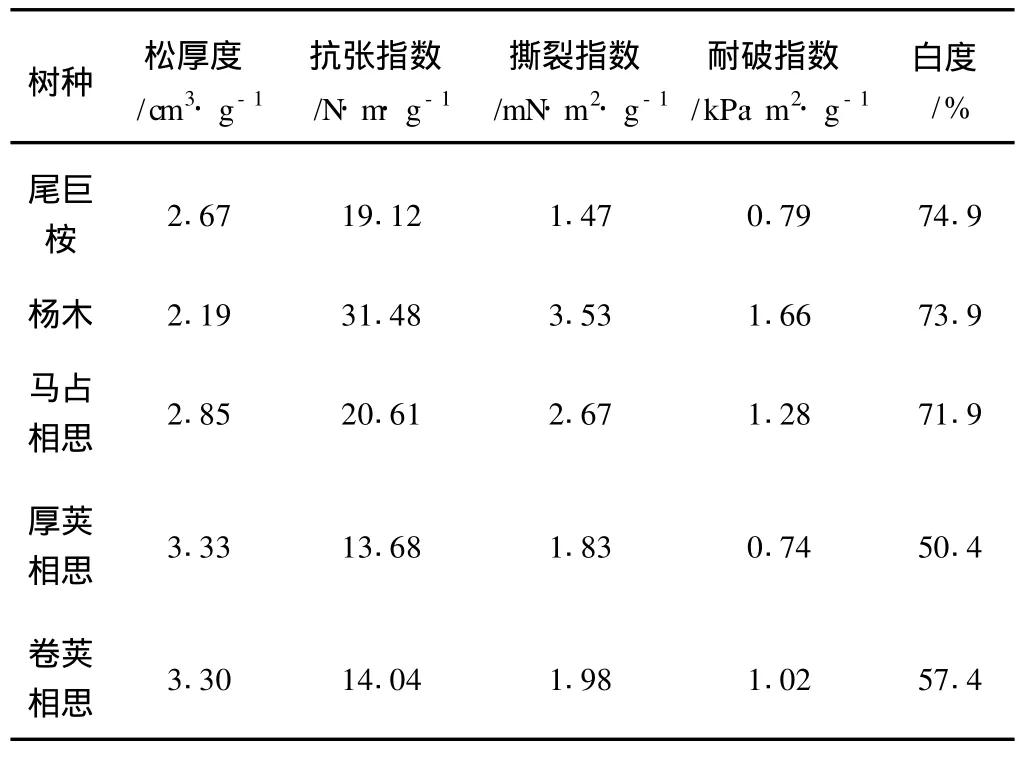
表2 5种原料P-RC APMP性能
用GPPIM算法中的步骤(1)~(4)计算,其中GA算法采用格雷码编码[6],选定父代初始种群规模为n=100,最大进化代数eranum=300,交叉概率pc=0.80,变异概率pm=0.50,求得最佳投影方向a*(0.3630,0.4878,0.4835,0.4278,0.4621)最大投影目标函数值Q(a*)=0.6184。根据得到的a*,按式(2)计算各样本最佳投影值与对应等级的散点图见图1。从图1可以看出,z*(i)与y(i)的图形为阶梯形下降曲线,即投影值越大,级别值越小,质量越好。各阶梯左右两端点A~J的坐标分别为(0.0368,5),(0.2764,5),(0.4503,4),(0.6875,4),(0.8642,3),(1.1184,3),(1.2760,2),(1.5248,2),(1.7398,1),(2.1203,1)。现用这10个点进行分段线性插值,可作为纸浆质量综合评价的数学模型。为描述方便,现把A~J这10个点构成的5条线段AB,CD,EF,GH,IJ按如下集合表示:
{c1(k),c2(k),d(k)},k=1,2…,N
其中,c1(k)、c2(k)分别对应图1中各线段左、右端点横坐标值,d(k)为各线段对应评价等级值(纵坐标),本例中,d(k)=N-k+1,N=5,则GPPIM的纸浆质量评价模型为图1中折线所对应的函数,可用式(8)表示。
表2各待评价样品数据按式(1)进行归一化处理后,再和a*一起代入式(2),计算各样品最佳投影值,最后用式(8)就可求出各树种纸浆质量的等级值,结果见表3。为便于对比,表3列出了文献[2]中模糊评价结果,其中模糊评价计算等级和排序根据各样本综合评价结果向量平方和加权平均[9]求得。
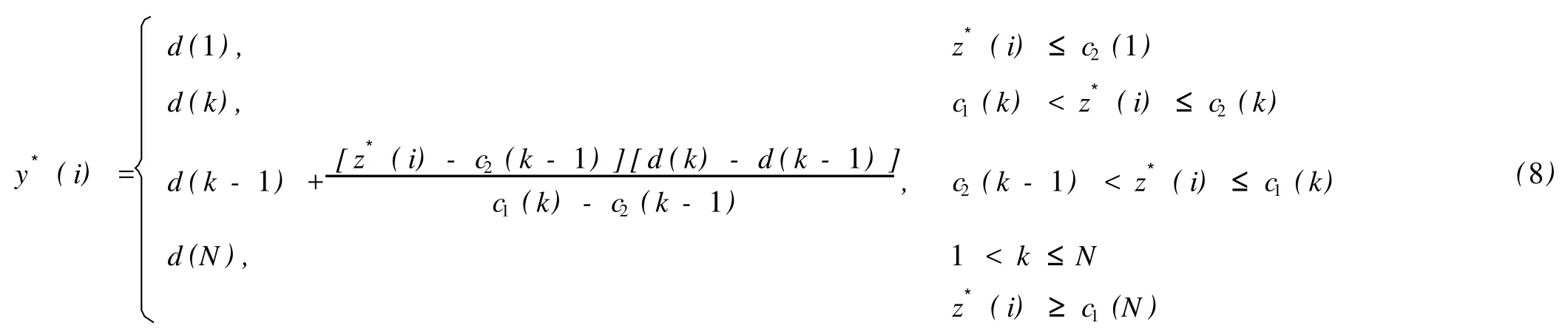
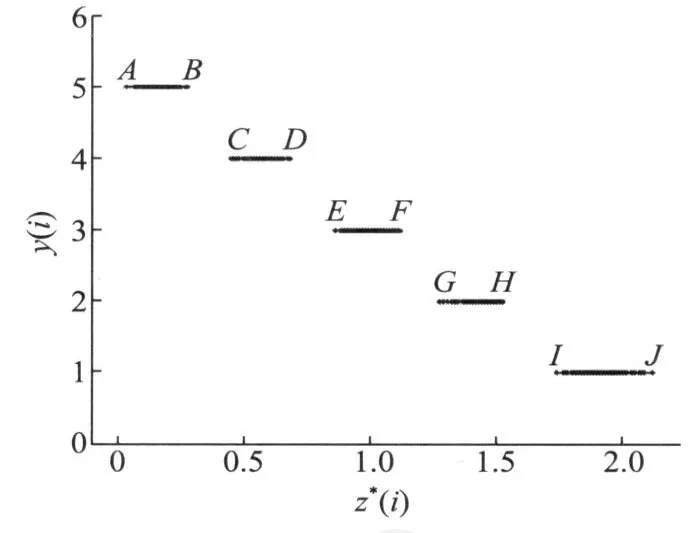
图1 最佳投影值z*(i)与经验等级y(i)的散点图
从表3的GPPIM等级计算值可以得出结论:杨木浆质量较高(Ⅱ级),马占相思木浆质量中等(Ⅲ级),厚荚相思木浆质量较差(Ⅳ级),尾巨桉和卷荚相思木浆在中等(Ⅲ级)和较差(Ⅳ级)之间,其中尾巨桉木浆偏向中等(Ⅳ级),卷荚相思木浆偏向较差(Ⅳ级)。由于最佳投影值与等级值的图形为阶梯形下降曲线,可以得出最佳投影值越大的树种生产的纸浆质量越好的结论,所以从表3各树种的最佳投影值可以看出,5个树种生产的纸浆质量从好到坏的顺序为:杨木>马占相思>尾巨桉>卷荚相思>厚荚相思。GPPIM评价结果与模糊综合评价方法基本一致,仅在尾巨桉和卷荚相思排序上有差异,由于两者处于中等(Ⅲ级)和较差((Ⅳ级)之间的模糊地带,存在这种差异也是可以理解的。本例中由于尾巨桉木浆白度是5个样本中最高的,且比卷荚相思木浆白度高17.5个百分点,而其他指标和卷荚相思木浆比虽各有高低,但相差不大,因此GPPIM方法判断尾巨桉浆比卷荚相思木浆综合质量稍好应更为合理。此外,最佳投影方向各分量绝对值的大小实质上反映了各指标各树种纸浆质量评价的影响程度,各分量绝对值越大,则对质量评价影响就越大,据此可以进一步检验分级标准的合理性。
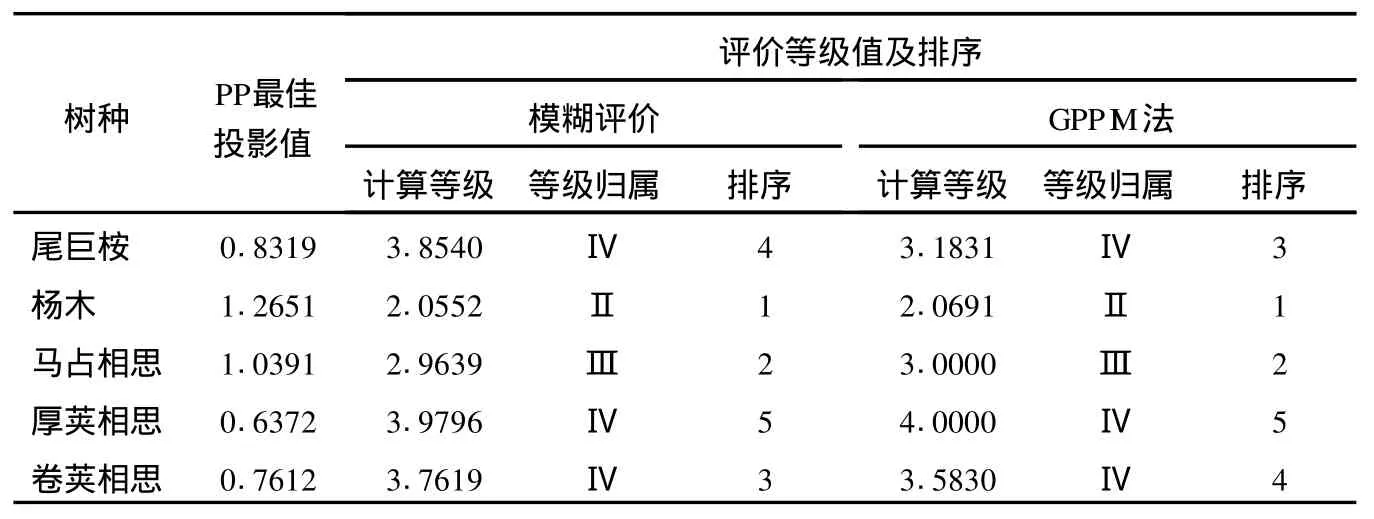
表3 5种原料P-RC APMP质量评价结果
4 结论
4.1 采用遗传投影寻踪插值模型(GPPIM)方法直接从纸浆质量评价等级标准出发,由样本数据驱动,把纸浆质量多维评价指标综合成一维投影指标,建立纸浆质量评价的数学模型,较好地实现了对速生材制高得率浆的综合评价。方法不需要设计隶属函数,简便直观,并可适用于其他类似纸浆的评价。模型建立和评价中无需人为干扰,结果具有较好的客观性。
4.2 由于最佳投影值与等级值的图形为阶梯形下降曲线,可以得出最佳投影值越大的纸浆,其对应质量越好的结论。对于多个纸浆样本混合评价问题,GPPIM方法既可以利用等级值从整体上来判别纸浆所属等级,又可以利用最佳投影值对处于同一等级或模糊区域的样品进行细致评价,兼具较强的分类功能和较好的排序功能,提高了纸浆质量评价问题各层次的分辩力。
4.3 采用的纸浆等级评价标准是在相同工艺条件下划分的,相对来讲并非是最佳选择。因为不同原料最佳制浆工艺不相同,即使是相同原料,不同的产地也可能会导致制浆工艺的不同。因此,在今后的进一步研究中,将考虑建立不同原料最佳制浆条件下的纸浆性能分级标准,由此建立的GPPIM模型得到的评价结果应更具有实际意义。
[1]唐孝华,房桂干.速生树种制浆造纸适应性能评估模型的研究[J].林产化学与工业,1996,9(16):60.
[2]璩爱玉,房桂干.模糊数学方法在高得率浆评价中的应用[J].中国造纸学报,2008,23(2):105.
[3]杜 栋,庞庆华.现代综合评价方法与案例精选[M].2版.北京:清华大学出版社,2008.
[4]金菊良,张欣莉,丁 晶.评估洪水灾情等级的投影寻踪模型[J].系统工程理论与实践,2002,22(2):140.
[5]王顺久,李跃清.投影寻踪模型在区域生态环境质量评价中的应用[J].生态学杂志,2006,25(7):869.
[6]杨晓华,沈珍瑶.智能算法及其在资源环境系统建模中的应用[M].北京:北京师范大学出版社,2005.
[7]雷英杰,张善文,李续武,等.Matlab遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[8]项静恬,史久恩.非线性系统中数据处理的统计方法[M].北京:科学出版社,2000.
[9]胡永宏,贺思辉.综合评价方法[M].北京:科学出版社,2000.

