木片浸渍程度数学建模
吕卫军 曹春昱 薛崇昀 刘锡炳 黎的非 张 勇
(1.中国制浆造纸研究院,北京,100020;2.赤天化纸业股份有限公司,贵州赤水,564700)
对于化学浆和化学机械浆,化学药品在木片中的渗透和扩散起着至关重要的作用。浸渍影响化学药品在木片中分散的均匀性,最终影响制浆时间、能耗和成浆质量[1-2]。化学药品在木片中的传递主要通过两个机理完成:①压力梯度作用下的渗透机理,指液体进入木片孔隙的过程;②浓度梯度作用下的扩散机理,指离子或可溶性物质以水为介质向木片内部扩散的过程[3-5]。
在早期的研究中,研究者采用定性和定量的研究方法和技术,从实验条件、木材结构和浸渍液体的性质等方面对影响木片浸渍过程的因素进行了大量的探讨[4,6-8]。随后几十年,虽然研究者对制浆及后续过程进行了重点开发研究,但木片浸渍过程的研究及相关技术的应用并没有实质性改变。近年来,随着人们对蒸煮前和机械处理前预浸渍重要性认识的提高,一些研究者试图对木片浸渍建立数学模型,以期进行深入研究[9-11]。但大部分数学模型是建立在单独采用Poiseuille或Darcy法则和一些假设的基础上,计算过程复杂且测定结果与实际情况有所偏差。因此,在对木片浸渍过程进行数学建模时,需要综合考虑液体的渗透和扩散过程。从这个观点来看,建立一个综合的木片浸渍程度数学模型对于木片浸渍工艺的优化是非常必要的。
1 木片浸渍程度数学模型的建立
1.1 木片成分的划分
木片是一种多孔介质。在自然状态下,木片由可溶性物质(下标“s”)、不溶性物质(下标“ns”)、孔隙中的气体(下标“g”)和孔隙中的液体(下标“l”)4部分组成,其关系如图1所示。其中,木片质量(m)、体积(V)和密度(ρ)的下标“c”、“dc”、“v及“w”分别表示自然状态、绝干状态、孔隙及固态物质。
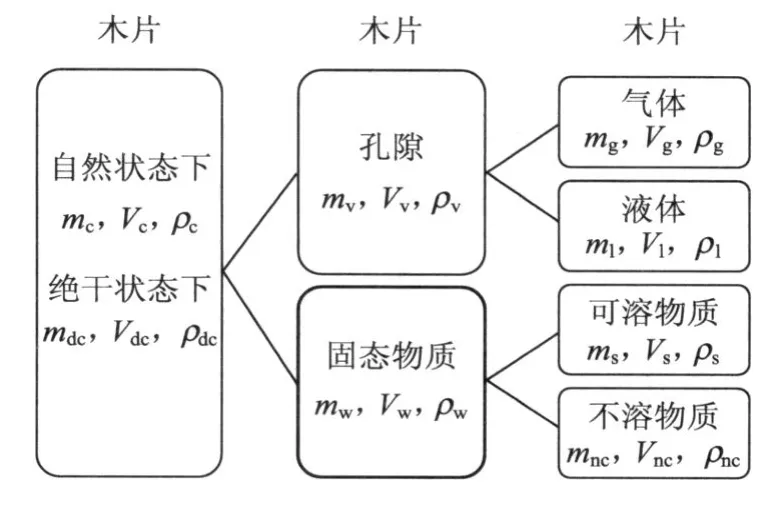
图1 木片组成关系
1.2 相关问题的假设
对木片浸渍过程进行数学建模是一项非常困难的工作。首先,木材是非均一三相体系的物质,液体从不同方向向各向异性的木片内部浸渍需要依靠不同的机理来完成[12-13];其次,浸渍过程可能伴随众多复杂的现象,如非线性流体流动、毛细管蒸汽冷凝、气液界面张力、气体溶解与扩散、结合水迁移、木材润胀和木材与液体的其他化学作用等[14-16]。合理地假设可以简化数学建模过程。因此,在先前理论及实验基础上,作如下假设:
(1)低温时,木片浸渍前后体积和木片所包含物质不发生变化。
高温能加速木片在浸渍液中的润胀,木片中包含的部分物质也会在浸渍液中发生水解。然而,在低温(低于100℃)和短时间处理条件下,木片体积的变化和木片所包含物质的损失不大,实验时可以忽略[11,17]。
(2)木材的骨架密度(ρw=mw/Vw)对于不同材种恒为相应的常数。
木材的基本密度(木材在含水量饱和状态下的密度)随原料和产地不同变化较大[18]。有资料显示,木材的骨架密度随原料和产地的不同,在1.46~1.53g/cm3的范围内变动,但接近于一个常数[19-20]。木材的骨架密度由组成木材的纤维素、半纤维素、木素和其他低分子质量物质在木材中的比例决定。为特定的目的,可假设木材的骨架密度为常数。
(3)整个浸渍过程为等温过程。
假设整个浸渍过程为等温过程,木片浸渍过程中截留在孔隙中的气体就遵守相应温度下的理想气体状态方程。
(4)液体向木片内部浸渍过程中,压缩气体体积被等体积的液体所取代,即Vv=Vl+Vg=常数。
木片中的毛细管系统具有一定几何形状和体积,在液体与木片接触的初期,截留气体有可能在浸渍液的推动下逃逸出木片孔隙。在浸渍液向木片浸渍过程中,绝大部分截留气体最有可能通过溶解和扩散的方式逃逸出木片孔隙,且这个过程相对来说要慢许多。因此,本研究假设截留气体在受到外界压力作用下体积发生变化时,变化部分的体积会被等体积浸渍液代替。
(5)木片的结合水和自由水密度相同,如浸渍液为非纯水溶液,在整个浸渍过程中,其密度不发生变化。
水在木片中以3种状态存在,即存在于毛细管中的自由水、存在于无定形区的结合水和水蒸气[3,21]。资料表明,结合水的密度为1.01g/cm3,仅比自由水的高1.0%~2.0%[19],因此,结合水和自由水的物理性质差别在本研究中可以忽略。Zanuttini等的研究结果表明,用10g/mL的NaOH处理木片40min,由木片内外浓度差引起的浸渍液密度变化在1.5%~2.0%之间[1],这种变化在本研究中也予以忽略。
1.3 常压木片浸渍程度数学模型
木片与浸渍液接触后,其孔隙会部分或全部被浸渍液占据。木片浸渍程度(Ⅰ)定义为木片中的孔隙被浸渍液取代的比率,即:

根据木片浸渍程度的定义,0<I<1。由图1中的体积关系可知:

由假设可知Vc=Vdc,根据密度定义ρ=m/V,等式(2)可以写为:

在绝干状态下,由于存在于木材孔隙中的气体质量mg≪mw,所以mdc≈mw,等式(3)可以写为:

将等式(4)代入等式(1)中,则:

因为Vl=ml/ρl,等式(5)可表达为:

等式(6)即为常压下木片浸渍程度的数学模型,其中:
ρl为浸渍液的密度,g/cm3,如果浸渍液是水,其密度约为1g/cm3。
ρdc为木材的绝干密度,g/cm3,不同材种绝干密度不同。
ρw为木材的骨架密度,g/cm3,文献[19-20]中给定值为1.50g/cm3,也可以采用孔隙率测定仪实际测值。
ml/mdc为木片中水分与木片绝干质量的比值。
1.4 压力木片浸渍程度数学模型
木片中的气体在浸渍开始时会被封堵在木片中,在有压力的情况下,被封堵在木片中的气体体积Vpg会发生变化,从而影响木片浸渍程度。下面将对压力存在下的木片浸渍程度进行推导。
由理想气体状态方程可知:

其中,P0为初始压力,P为浸渍压力。因为Vv=Vl+Vg=常数,所以:
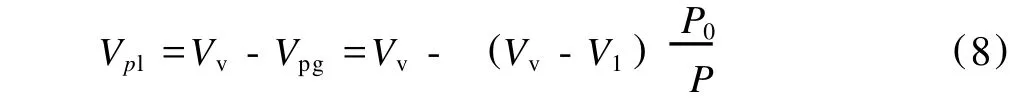
其中,Vpl为有压力存在时,孔隙中液体的体积。根据木片浸渍程度的定义可知:
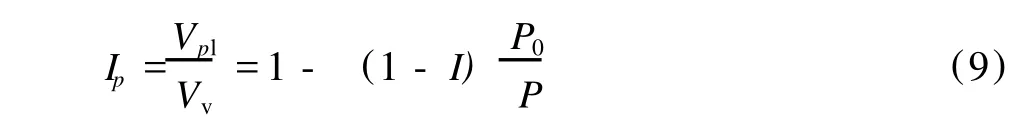
其中,Ip为压力状态下的浸渍程度。将等式(6)代入等式(9),结果为:
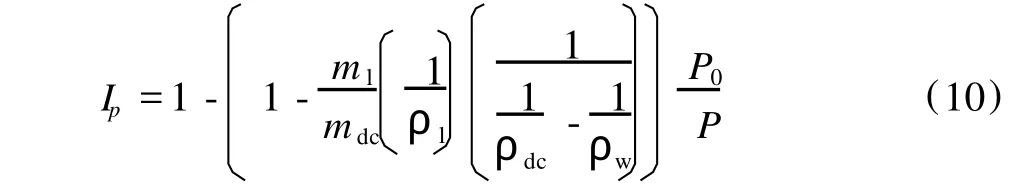
等式(10)即为压力状态下木片浸渍程度的数学模型。
2 实验
2.1 原料与仪器
原料:红松、杨树、桉树、相思树、竹,自然干燥。
仪器:游标卡尺(0.02mm),空隙率测定仪(AutoPoreⅣ 9500),秒表,天平(0.0001g),水浴锅。
2.2 实验方法
2.2.1 木片骨架密度、孔隙率及绝干密度测定
将原料样品切成8mm×8mm×8mm的小方块,每块样品约0.2g,取样过程中要尽量避免材料受压,样品须在105℃烘干至恒重,然后采用AutoPoreⅣ9500孔隙率测定仪测定原料的骨架密度和孔隙率。其中,最高进汞压力为206.8MPa。
木片的绝干密度按照GB/T1933—1991进行测定。
2.2.2 木片实际浸渍程度的测定
取红松片60mm×60mm×3mm若干,红松片需六面刨光,将其放入无干燥剂的干燥器中平衡水分备用。将平衡水分后的红松取出,迅速用游标卡尺测定其体积,随后将红松片完全浸入温度25℃、NaOH浓度0.5mol/L(密度1.02g/cm3)的浸渍液中,在规定的时间内取出(木片取出时间为2.5、5.0、10.0、15.0、25.0、30.0、45.0、60.0、120.0、180.0min),在表面无液滴滴落时称取红松片质量,最后在105℃烘至恒重,测定绝干质量。
80℃时的测定方法与25℃时的相同。
木片实际浸渍程度的计算方法为:

其中,孔隙率为63.3%(AutoPoreⅣ9500测定值)。
2.2.3 数学模型推导木片浸渍程度的计算
计算公式采用等式(6),其中ρw=1.35g/cm3(AutoPoreⅣ 9500测定值),ρdc=0.47g/cm3。
2.2.4 数据处理
采用Origin7.5对所得数据进行处理。
3 结果与讨论
3.1 木材骨架密度
本实验对不同材种的骨架密度进行了测定,结果见表1。
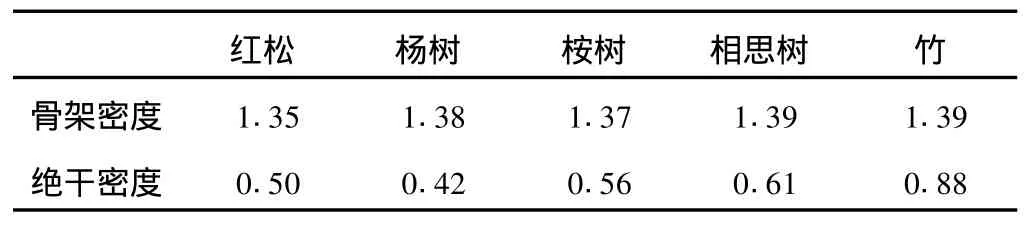
表1 不同材种的骨架密度和绝干密度 g/cm3
本实验也对毛白杨不同部位的骨架密度进行了测定,取样部位如图2所示,测定结果见表2,其中“sap”代表边材,“heart”代表心材。
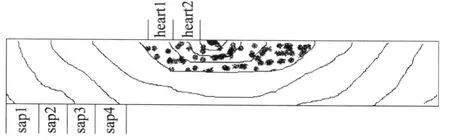
图2 毛白杨不同部位取样示意

表2 毛白杨不同部位的骨架密度 g/cm3
压汞法对于评价多孔介质来说不是一项新技术,汞入侵实验为三维多孔介质提供了一种测量孔隙体积和计算纤维表面积的方法[22]。而用压汞法来计算多孔介质(如木材)的骨架密度是压汞法的另外一个用途,但相应的研究和报道却并不多见。
由表1可以看出,5种不同材种的绝干密度变化较大,绝干密度最大的竹与绝干密度最小的杨木之间相差110%。而骨架密度在1.35~1.39g/cm3之间变动。骨架密度最大的竹和相思树与骨架密度最小的红松之间相差仅3.0%。由表2可知,毛白杨不同部位的骨架密度在1.35~1.40g/cm3之间,最大值与最小值之间相差3.7%。本实验结果与文献中的给定结果并不完全吻合,可能原因是进汞压力不同引起的(AutoPoreⅣ9500实验最高进汞压力为206.8MPa),但对于不同材种和同一材种不同部位的骨架密度而言,变化并不明显。
3.2 木片浸渍程度数学模型评价
对木片浸渍程度数学模型进行评价是数学建模过程的重要步骤,评估可用以说明数学模型的可行性和适用范围。图3和图4为实际测定值和用木片浸渍程度数学模型计算的木片浸渍程度在不同温度下的结果。
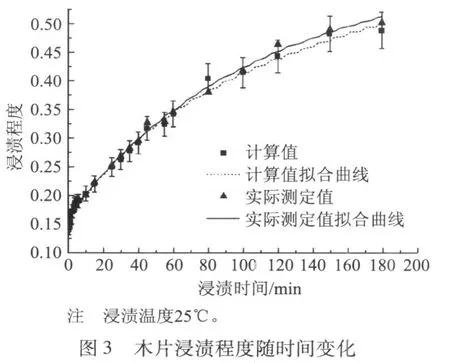
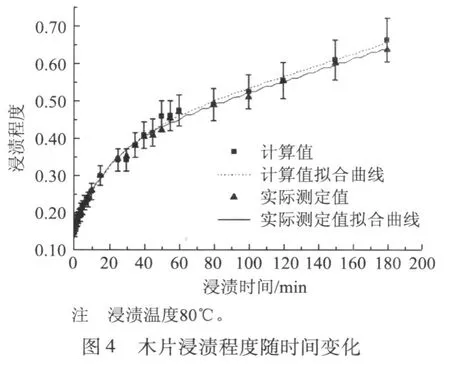

表3 非线性拟合曲线的相关参数
对图3和图4所得数据采用Origin7.5进行处理,得到不同温度下的实际测定值和用木片浸渍程度数学模型计算浸渍程度的拟合方程为:
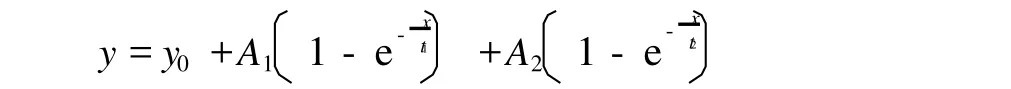
该方程所对应参数值如表3所示。其中,25℃时计算值与实际测定值之间的最大误差为6.4%,80℃时计算值与实际测定值之间的最大误差为8.7%。由图3和图4可知,木片浸渍程度数学模型的计算结果较为客观地反映了木片在实际情况下的浸渍程度。
4 结论
4.1 在对木片成分进行划分和合理假设的基础上建立了计算木片浸渍程度的数学模型。木片浸渍程度数学模型不必考虑渗透和扩散这一复杂动态过程,只对浸渍结果进行计算。通过对这个数学模型所测定结果的计算机处理,得到了不同处理条件下的非线性拟合方程。木片浸渍程度数学模型可以用于准确地表征木片在浸渍液中的浸渍程度,从而简化和方便木片浸渍工艺的优化。而且,木片浸渍程度数学模型表达方程中无体积项,从而可以用来计算不规则形状木片的浸渍程度。
4.2 可以单独使用木片浸渍数学模型对木片某一点的浸渍程度进行计算,也可以对多个点进行数学模型计算后采用非线性方程进行拟合,然后从坐标轴上直接读取木片某一点的浸渍程度。因为非线性模拟可以在一定程度上抵消由实验带来的误差,所以更为科学和准确。
4.3 由于第一个假设在高温和高碱浓条件下与实际情况相差甚远,因为存在于浸渍液和木材中的化学物质会发生反应,从而会导致计算结果与实际测定结果误差增大。基于以上原因,建议在高温和高碱浓条件下使用木片浸渍程度数学模型时需谨慎。
[1]ZanuttiniM,CitroniM,MarzocchiV.Pattern of alkali impregnation of poplar wood at moderate conditions[J].Holzforschung,2000,54(6):631.
[2]Johansson L,Pengi F F,Simonson R,et al.The effects of chip pretreatment on CT MP pulp properties[J].Paperi.Ja.Puu.,1999,81(8):559.
[3]Stamm A J.Diffusion and penetration mechanis m of liquids into wood[J].Pulp and Paper Magazine of Canada,1953,54(2):54.
[4]Stone J E,FörderreutherC.Study of penetration and diffusion into wood[J].Tappi Journal,1956,39(10):679.
[5]Stone J E,Green H V.Penetration and diffusion into hardwood[J].Tappi Journal,1959,42(8):700.
[6]Stone J E.The effective capillary cross-sectional area of wood as a function of pH[J].Tappi Journal,1957,40(7):539.
[7]Mckibbins SW.Application of diffusion theory to thewashing of kraft cooked wood chips[J].Tappi Journal,1960,43(10):801.
[8]Malkov S,Tikka P,Gullichsen J.Towards complete impregnation of wood chipswith aqueous solutions,part1:a retrospective and critical evaluation of the penetration process[J].Paperi.Ja.Puu.,2003,85(8):460.
[9]Robertsen L,LönnbergB.Diffusion in wood,Part1:theory and apparatus[J].Paperi.Ja.Puu.,1991,73(6):532.
[10]Costanza V,Miyara A J.Dynamics of hardwood impregnation[J].Holzforschung,2000,54(2):183.
[11]Mantanis G I,Young R A,Rowell R M.Swelling ofwood,part 1:s welling in water[J].Wood Science and Technology,1994,28(2):119.
[12]ParanyiN I,RabinovitchW.Determination of penetration rate of liquid media intowood using a quartz spiral balance,partⅠ:water and an air-dry spruce[J].Pulp and PaperMagazine of Canada,1956,56(3):164.
[13]Rudman P.Study in wood preservation,partⅠ:penetration of liquids into Eucalypt sapwoods[J].Holzforschung,1965,19(1):5.
[14]Lu J X,Avramidis S.Non-darcian air flow in wood,partⅡ:nonlinear flow[J].Holzforschung,1999,53(1):77.
[15]Wardrop A B,Davies G W.Morphological factors relating to the penetration of liquids into wood[J].Holzforschung,1961,15(5):129.
[16]MaassO.The problem of penetration[J].Pulp and Paper Magazine of Canada,1953,54(8):98.
[17]Mantanis G I,Young R A,RowellR M.Swelling of wood,part Ⅲ:effect of temperature and extractives on rate and maximum swelling[J].Holzforschung,1995,49(3):239.
[18]Feamside PM.Wood density for estimating forest biomass in Brazilian Amazonia[J].Forest Ecology and Management,1997,90(1):59.
[19]Malkov S Y,Kuzmin V A,Baltakhinov V P,et al.Modeling the process of water penetration into softwood Chips[J].Journal of Pulp and Paper Science,2003,29(4):137.
[20]Malkov S,Tikka P,Gullichsen J.Towards complete impregnation of wood chips with aqueous solutions,part2:studies on water penetration into softwood chips[J].Paperi.Ja.Puu.,2001,83(6):468.
[21]Almeida G,GagnéS,Roger E,et al.A NMR study ofwater distribution in hardwoods at several equilibrium moisture contents[J].Wood Science and Technology,2007,41(4):293.
[22]Rucinski K,Caronia A,Mcneil R.Filtermedia characterization by mercury intrusion[J].Tappi Journal,1986,23(11):121.

