用函数拟合方法实现热偶规的非线性标定

李 杨,乔 双

(东北师范大学物理学院,吉林长春 130024)

用函数拟合方法实现热偶规的非线性标定

李 杨,乔 双

(东北师范大学物理学院,吉林长春 130024)

利用高次函数拟合处理热偶规传感器的非线性特性.所得函数直接写入热偶真空计单片机,用其处理热偶规采样数据.实验结果表明,其方法稳定性、精确性、速度均达到良好效果.

真空测量;传感器;非线性特征;函数拟合

真空技术是现代科学技术的一个重要组成部分,它推动并促进了科技研究和生产技术的发展,而真空测量是真空技术的一个重要环节.作为真空度测量设备的真空计类型很多,其灵敏度、量程和用途各不相同[1].

热偶真空计是在低真空测量中广泛应用的一种测量仪器.热偶真空计以热偶规管作为传感器,将被测环境的压强信号转换为微弱的电信号,经过信号放大和A/D转换,送入单片机数据处理、显示.热偶真空计以其性能稳定、价格适中等优点被广泛应用于低真空测量领域,但由于热偶规这种传感器存在着较强的非线性,致使在数据处理上存在一系列的问题.为了提高测量精度,必须对其非线性进行处理.用传统数值计算方法处理,计算量繁重、过程冗杂[2-4].

M athematica软件比传统数值计算方法具有很多优点.Mathematica软件是美国Wolfram公司开发的一个高度集成化的计算机软件系统.它的主要功能包括数值计算、符号运算、数据处理和图形绘制.由于该软件功能强大、界面友好和使用简单,与Matlab和M ap le一起被称为当今世界上最优秀的三大科学计算软件.M athematica软件从1987年问世至今,已经发展到5.2版本,它可以在各种操作系统、工作站和网络上使用[5].M athematica不仅能完成高级语言所具有的数值计算,还能完成复杂的数学公式推导和理论分析,能完成图形可视化等高级功能.M athematica软件中的高次函数拟合主要利用最小二乘分析,将数值与要拟合的函数做分析运算,以求出最接近或最能表示数据趋势的函数[6].

本文采用Mathematica数学软件中高次函数拟合功能,来拟合热偶规传感器的非线性特性.

1 热偶规真空测量基本原理

图1 热偶规结构示意图

热偶规是利用气体的热传导现象来测量气体真空度的(见图1).工作时给热偶规加热丝通入一恒定电流,由热电偶来测量加热丝温度.真空度低时压强高,气体分子多,导热性能好,加热丝散失的热量多,所以加热丝温度低;真空度高时压强低,气体分子少,导热性能下降,加热丝温度高.将热电偶输出的热电势转换为压强值就实现了真空度的测量.

测量过程中压强值是热电偶输出热电势的函数,其公式为

其中:v是热电偶输出值;p是压强值.热电偶输出值v与压强值p之间存在着一定程度的非线性.想利用热偶规作为传感器精确测量压强,就必须对其非线性进行处理.

2 Mathematica数学软件函数拟合

热偶规有效工作范围大都分布在10-1～102Pa,我们针对所使用的规管在其量程内,用高精度真空计选取充分多的测量点进行测量,记录下每个测量点的气压值和传感器对应的电压值.将测量点数据按照传感器输出电压增序填入坐标列表,如表1所示.

表1 热偶规测量数据

将n组坐标输入到M athematica软件,利用命令对其处理,详细方法可查询M athematica数学软件工具书.

下面是利用Mathematica软件分析、处理16组数据并拟合出优质函数的例子:

图2 Mathematica软件数据处理函数图

我们通过以上函数图像可以看出随着拟合次数的增加(见图2),函数更加优化,抽样点数据与拟合函数十分吻合.我们可根据实际精度需要和硬件情况选择最适合的拟合次数,最后将拟合的最优函数写入真空计单片机系统,完成真空计的标定.

3 实验效果分析

为验证该方法的可行性,我们以ZJ-51型热偶规为研究对象,做了一系列数据采集、对比、分析实验.

实验由热偶规、信号放大电路、A/D转换电路、LED显示电路、MCS-51单片机系统组成自制真空计,以高精度真空计为校正标准.实验基本步骤是以真空泵抽取真空测量环境,采用热偶规为传感器,将被测环境的压强信号转换为电信号,经信号放大电路放大为A/D转换电路所需标准信号直流电压0～10 V,12位A/D与0～10 V的对应输出数据d为0～4 096,其测量压强范围为10-1～65 Pa[7].我们在其量程范围内测定并记录20组数据见表2,其中d为LED显示的A/D值,pA为高精度真空计测得真空环境压强值,pB为软件拟合函数计算压强值.

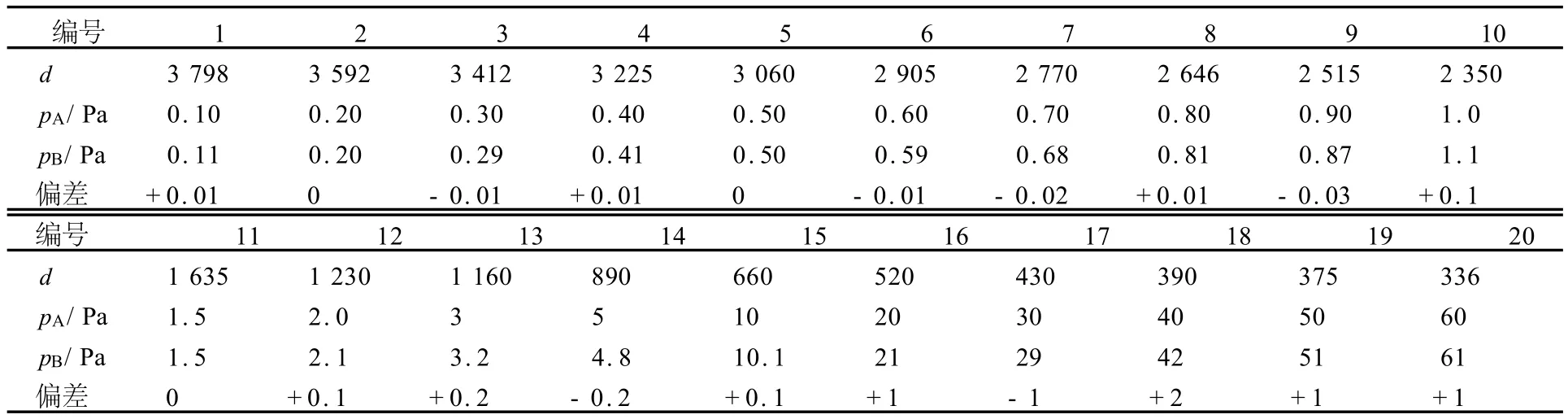
表2 热偶规测量与拟合数据

在整个实验过程中,自制热偶真空计系统稳定性、运算速度均达到要求,通过与标准真空计数据对照十分吻合.实验表明,采用M athematica数学软件进行高次函数拟合真空测量中热偶规传感器的非线性的方法是切实可行的,测量精度能够满足实际需要.

4 结束语

经过大量实验和实际应用验证,利用M athematica数学软件进行高次函数拟合真空测量中热偶规传感器的非线性的方法十分有效,且简单、可靠.此方法与现行的复杂算法相比,去繁就简,可以在保证测量精度的同时节省科研人员大量精力.另外,此方法不局限于处理真空测量中热偶规传感器的非线性拟合问题,也可应用于其他工程、科研领域中非线性问题.

综上所述,Mathematica数学软件进行高次函数拟合真空测量中热偶规传感器的非线性的方法,切实可行并具有较好的应用前景.

[1] 王逊.常用真空计的测量范围及其性能[J].真空,2004,41(4):47-48.

[2] 李有法,李晓勤.数值计算方法.第2版.[M].北京:高等教育出版社,2005:70-101.

[3] 常晶,刘冬.非线性常微分方程的多项式逼近[J].吉林大学学报:理学版,2010,48(3):367-370.

[4] 邓义华.非线性中立型延迟积分微分方程单支方法的数值稳定性[J].东北师大学报:自然科学版,2009,41(2):53-57. [5] 张隽,沈守枫,潘祖梁.数学物理方程与Mathematica软件应用[M].北京:机械工业出版社,2008:188-195.

[6] 洪维恩,魏宝琛.数学运算大师Mathematica 4[M].北京:人民邮电出版社,2002:154-182.

[7] 李华.MCS-51系列单片机实用接口技术[M].北京:北京航空航天大学出版社,1993:262-416.

Using function fitting method to achieve non-linear calibration of thermocouple gauge

L I Yang,Q IAO Shuang

(School of Physics,Northeast No rmal University,Changchun 130024,China)

This paper introduces a method of using high-o rder function fitting directly to deal w ith the thermocoup le gauge senso r nonlinear.The go tten function is directly w ritten into thermocoup le vacuum gauge SCM,w hich is used to deal w ith samp le data of thermocoup le gauge.Experimental results show that the stability,accuracy and speed of thismethod are good,and the method is feasible.

vacuum measurement;sensors;non-linear characteristics;function fitting

TP391

510·10

A

1000-1832(2010)04-0062-04

2010-08-25

国家科技支撑计划项目(2008BAA 15B03).

李杨(1984—),男,硕士研究生;通讯作者:乔双(1963—),男,博士,教授,主要从事核电子学、嵌入式应用、图像处理与模式识别研究.

(责任编辑:石绍庆)