基于折叠结构的半带滤波器的设计*

叶巧文，林 伟

(1.福建省微电子与集成电路重点实验室， 福州350002；2.福建省微电子与集成电路重点实验室，福州 350002)

作为软件无线电的核心技术[1]——上下变频技术[2]可以通过专用芯片来实现。目前市场上的DDC、DUC品种很多，尽管这些专业芯片的功能强大但其价格昂贵，工作参数配置非常的复杂，且由于当前的通信制式多种多样，专用芯片无法完全满足软件无线电系统的性能指标。而FPGA，即现场可编程门阵列，拥有丰富的逻辑资源，可编程性强，可以用于复杂的数字信号处理[3-6]比如卷积、相关和滤波等等，为此采用FPGA[7-8]来实现数字上下变频是目前软件无线电通信系统的主要实现方案。

数字上下变频由各种多采样率数字滤波器组成，常见的滤波器有CIC滤波器、半带滤波器、FIR整形滤波器等。半带滤波器(Half-Band)是一种特殊的FIR滤波器，由于其系数的对称性以及将近一半系数为零值，这使得其滤波运算过程中乘法次数减少近3/4，加法次数减少近一半，同时用于存储系数的存储器也减少了一半，因此半带滤波器是个高效的数字滤波器，特别适合实现2的幂次方倍的抽取或者内插，有计算效率高，实时性强等特点。流行的半带滤波器系统级设计方法主要是在MATLAB环境下根据设计要求搭建系统，用system generator系统设计工具，将模型直接转化成代码，然后进行调用，此方法实现起来比较简单，一般能够满足要求但其存在着功耗高、面积大、资源耗费代价高等不足之处。为了弥补上述不足，本设计首先根据设计要求用MATLAB产生相应的滤波器系数，然后采用折叠结构，通过代码[9-10]编写来实现。

1 半带滤波器的设计原理

半带滤波器(HB)是一种特殊的FIR滤波器，其频率响应满足公式1的FIR滤波器。

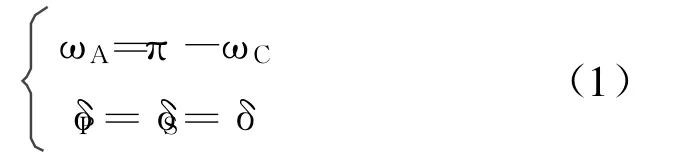
FIR滤波器可以表示为：

根据公式2，通常半带滤波器 可以采用直接型或者转置型结构来实现。由于h(k)=h(N-1-k)，采用转置型结构可以减少乘法器以及加法器的使用，其结构图如图1所示。

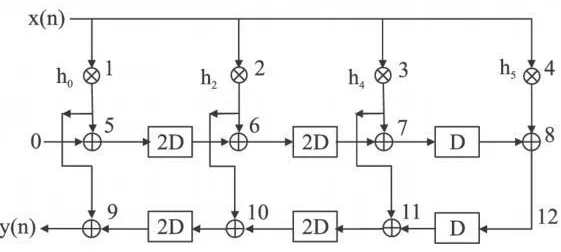
图1 转置型FIR滤波器的结构图

2 基于折叠结构的半带滤波器的设计

2.1 折叠技术的原理

半带滤波器用作抽取器使用时，其输出速率为输入速率的一半，即输出速率与系统时钟频率是1∶2的关系，因此可以把转置型的半带滤波器进行折叠，折叠因子为2。为了使得折叠后时序不会出错，我们首先得算出折叠后各结点之间的延迟值，延迟可按照公式3进行计算。

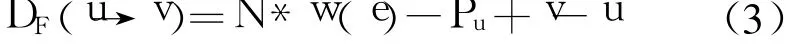
其中DF(u→v)指折叠后功能单元u的输出到功能单元v的输入所经过的延时数， N为折叠因子即折叠后功能单元迭代的次数， w(e)是折叠前功能单元u和功能单元v之间的延时数， Pu是功能单元u的流水级数， v和u分别是功能单元v和u的编号。计算出各个结点延迟值后我们就可以得到相应的结构图，然后根据结构图编写代码。在下采样当中采用折叠技术，可以大大减少乘法器的使用，减少大量的乘法运算，减少了面积和功耗。

2.2 基于折叠结构的半带滤波器的设计

下面以一个基于折叠结构的11阶半带滤波器的设计为例来说明设计的可行性及优越性。

2.2.1 设计指标

设计指标：系统时钟为61.44 MHz，半带滤波器的阶数11 阶，系数为定点18位，滤波器通带要求1.23 M，阻带位置要求为30.72-1.75=28.97 M。

2.2.2 下采样数据率变换

半带滤波器作为抽取器[12]使用时，其抽取因子为2，即输出速率为输入速率的一半，也就是说输出速率与系统时钟频率是1：2的关系。为了采用折叠技术，同时也方便整个滤波过程的时序控制，首先我们利用系统时钟产生一个同步控制信号contr_rw。同步控制信号contr_rw的初始值为1，在每个系统时钟上升沿到来时，其值在0与1之间进行跳变，其它时候数值保持不变，也就是说在第一个系统时钟上升沿到来时， contr_rw的值由1跳变为0，此值一直保持着，直到第二个系统时钟上升沿到来时， contr_rw的值才由0跳变为1，同样此值也一直保持到第三个系统时钟上升沿到来时才发生跳变。由此可见contr_rw的值只有在系统时钟上升沿到来时才发生跳变，为此我们可以用此同步控制信号作为分路器(DEMUX)的选通开关把输入数据分成奇、偶2个通道，以此达到下采样数据率变换。当系统时钟上升沿到来时，如果同步控制信号contr_rw的值为0，则把输入数据送入奇通道，此时偶通道送入的是0值；如果contr_rw的值为1，则把输入数据送入偶通道，此时奇通道送入的是0值；紧接着在经过两级的数据率稳定之后，奇、偶2个通道的数据率均为系统时钟频率的一半，也就是说此时奇、偶通道均为每两个时钟变化一次数据。根据公式2，我们知道此11阶半带滤波器的输出为：

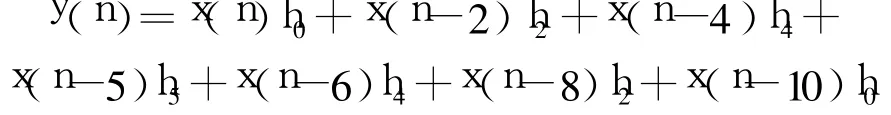
由此表达式我们知道x(n)h0、x(n-2)h2、x(n-4)h4、x(n-6)h4、x(n-8)h2、x(n-10)h0是根据奇通道数据产生的， x(n-5)h5是根据偶通道数据产生的。为了节约资源同时也为后续的折叠技术的应用，系数h2、h4采用分时复用技术，当同步控制信号contr_rw的值为0时产生系数h4、contr_rw的值为1时产生系数h2。

2.2.3 各结点延时单元计算

首先我们把设计当中用到的每个乘法器和加法器都当成一个结点，在应用折叠技术之前我们必须先知道各结点之间的延时值。如图1所示我们标注好每个结点的编号，为了让其结构具有对称性，我们把图1当中的结点12当成是一个加法器，此加法器的输入分别为：0值和结点8的输出值。由于时钟频率是输出速率的2倍，因此折叠因子N=2，此时所有编号为奇数的结点其u或者v值均为0，所有编号为偶数的结点其u或者v值均为1，根据公式3我们可以算出各个关键结点之间的延迟值为：DF(5→6)=5、DF(6→7)=3、DF(7→8)=3、DF(8→12)=0、DF(12→11)=1、DF(11→10)=5、DF(10→9)=3。根据这些延迟值，我们知道完成一次的滤波工作需要22个系统时钟和20个D触发器。为了能够以最快的速度完成滤波功能，这时可以引入重定时技术对D触发器进行分配，在满足时序的情况下减少D触发器的使用，从而减少延迟。重定时后各结点的延迟值为：DF(5→6)=3、DF(6→7)=1、DF(7→8)=1、DF(8→12)=0、DF(12→11)=1、DF(11→10)=3、DF(10→9)=1，也就是说采用重定时以后完成一次的滤波工作只需11个系统时钟和10个D触发器。于是根据这些延迟值我们便得到了折叠结构的结构图，如图2所示。

图2 基于折叠结构的半带滤波器的结构图

2.2.4 时序分析

图2当中的0表示同步控制信号contr_rw的值为0， 1表示同步控制信号contr_rw的值为1，为了方便分析，我们把图2当中的加法器按照从左到右，从上到下的顺序依次编号为加法器1、加法器2、加法器3、加法器4，用fm0mul_w表示通道送给加法器1的输入， 用 fm0add_r表示加法 器 1 的输出；用fm1mul_w表示通道送给加法器2的输入，用fm1add_r表示加法器2的输出，其它类推。接下来简要的分析下该设计是如何工作的。

第一个时钟Clock1：同步控制信号contr_rw的值为0，通道送入加法器1的数据为x(0)h0，加法器1的另一个输入值为0，此时加法器1 的输出值为x(0)h0；通道送入加法器2的数据为x(0)h4；通道送入加法器3的数据为x(0)h0；通道送入加法器4的数据为x(0)h4。

第二个时钟Clock2：同步控制信号contr_rw的值为1，通道送入加法器1的数据为x(0)h2；通道送入加法器2的数据为x(1)h5；通道送入加法器3的数据为x(0)h2；送入加法器4的数据为0。

第三个时钟Clock3、第四个时钟Clock4、第五个时钟Clock5、第六个时钟Clock6可按照此方法依此类推，具体时序参见表1。

第七个时钟Clock7：同步控制信号contr_rw的值为0，通道送入加法器1的数据为x(6)h0，加法器1的另一个输入值为0，此时加法器1 的输出值为x(6)h0；通道送入加法器2 的数据为x(6)h4，在Clock6产生的fm0add_r经过1个时钟延时成为此时刻加法器2的另外一个输入值，于是此时加法器2的输出值为x(2)h0+x(4)h2+x(6)h4；通道送入加法器3的数据为x(6)h0；通道送入加法器4的数据为x(6)h4，在Clock6产生的fm3add_r经过1个时钟延时成为此时刻加法器4的另外一个输入值，于是此时加法器4的输出值为x(0)h0+x(2)h2+x(4)h4+x(5)h5+x(6)h4。

第八个时钟Clock8、第九个时钟Clock9、第十个时钟Clock10 可以按此方法类推， 具体时序参见表1。

第十一个时钟Clock11：同步控制信号contr_rw的值为0，通道送入加法器1 的数据为x(10)h0，加法器1 的另一个输入值为0， 此时加法器1的输出值为x(10)h0；通道送入加法器2的数据为x(10)h4，在Clock10 产生的fm0add_r经过1个时钟延时成为此时刻加法器2 的另外一个输入值，于是此时加法器2的输出值为x(6)h0+x(8)h2+x(10)h4；通道送入加法器4的数据为x(10)h4，在Clock10产生的fm3add_r经过1个时钟延时成为此时刻加法器4的另外一个输入值，于是此时加法器4的输出值为x(4)h0+x(6)h2+x(8)h4+x(9)h5+x(10)h4。通道送入加法器3的数据为x(10)h0，在Clock10产生的fm2add_r经过1个时钟延时成为此时刻加法器3的另外一个输入值，于是此时加法器3的输出值为x(0)h0+x(2)h2+x(4)h4+x(5)h5+x(6)h4+x(8)h2+x(10)h0。

以上是基于折叠结构的11阶半带滤波器一个完整的滤波过程。具体的各个结点的时序如表1所示。

表1 时序表

3 仿真与实现

本设计采用Verilog语言编写，所采用的芯片是Xilinx公司的xc4vsx35-10ff668，用ISE10.1 和Modelsim进行仿真验证。仿真结果、综合报告图如图3、图4所示。从图3我们可以看出采用折叠技术的半带滤波器，其系数的产生以及最终滤波器的输出完全正确，完全满足我们的设计要求。传统的直接型半带滤波器的设计单单滤波过程，不包括系数的产生和抽取过程，需要10个D触发器、7个乘法器、6个加法器，而转置型半带滤波器则需要10个D触发器、4个乘法器、7 个加法器。然而从图4我们可以看到整个半带滤波器耗费的资源相当的少，总共用了13 个加法器， 16个寄存器。而由此可见采用折叠结构实现半带滤波器的设计能够大大减少资源的耗费， 而且整个过程没有用到乘法器只是用到少量的加法器和寄存器，减少了大量的乘法带来的额外的面积和功耗。同时本设计还经过硬件电路的验证，工作正常稳定，符合设计要求。

图3 基于折叠结构的11阶半带滤波器仿真图

图4 基于折叠结构的11阶半带滤波器综合报告图

4 结论

本文以11阶半带滤波器的设计为例，介绍了折叠技术在半带滤波器上的应用。与传统的设计相比其有很大的优越性和突破，单一时钟控制，并且设计过程当中没用到乘法器，大大减少了硬件资源，同时也使设计面积和功耗大为减少， 稳定性高！

[ 1] 成建晖.未来移动通信的软件无线电实现的研究[ D] .杭州：浙江大学， 2002.

[ 2] 赵国栋，郭德淳.基于FPGA的数宇中频接收系统[ M] .北京：北京理工大学出版社， 2006.

[ 3] 胡广书.数字信号处理理论、算法与实现[ M] .北京：清华大学出版社， 1997：281-296.

[ 4] 万国龙.数字信号处理[ M] .北京：清华人学出版社， 2007.

[ 5] 程佩清.数字信号处理教程[ M] .2版.北京：清华大学出版社， 2006.

[ 6] UweMeyer-Baese.数字信号处理的FPGA实现[ M] .刘凌，译.北京：清华大学出版社， 2006.

[ 7] 陈勇.基于FPGA实现高速专用数字下变频[ D].成都：电子科技大学硕士论文， 2005.

[ 8] 刘海兵，刘雄飞，张德恒.基于FPGA的数字滤波器的设计与实现[J].现代电子技术， 2006， 29(15)：70-70.

[ 9] 王金明.数字系统设计与Verilog HDL[ M] .2版.北京：电子工业出版社， 2005.

[ 10] Michael D.Ciletti.Verilog HDL高级数字设计[ M] .张雅绮，李锵，译.北京：电子下业出版社， 2005.

[ 11] 郭晓宇.基于FPGA实现FIR数字滤波器的研究[D] .武汉：武汉大学， 2004.

[ 12] 玛立，姚远程，张胡平.软件无线电接收机的多速率处理技术研究[J] .微计算机信息， 2008， (8)：283-284.