吡啶盐衍生物分子非线性光学性质的理论研究*

施 菊，朱 利，崔一平

(东南大学电子科学与工程学院先进光子学中心， 南京210096)

有机非线性光学(NLO)材料因其结构易裁剪性、电子响应快、光损伤阈值高、介电常数低和非线性极化率较大等优点，在全光器件、光存储和光信息处理等领域起着越来越重要的作用[1-2]。研究表明，有机分子的离域π电子以及分子内电子给体(D)和电子受体(A)间的电荷转移(CT)对非线性极化率起决定作用[3]，从分子角度设计和合成具有大的一阶超极化率β 的分子成为当前研究的热点。吡啶阳离子是最强的吸电子基团之一，在电子给体和共轭结构类似的情况下，吡啶盐衍生物的β 一般要比非离子型的中性分子高出几倍[4]，因此引起了实验和理论工作者的极大兴趣。

一般，实验研究NLO性质主要是通过电场诱导二次谐波(EFISHG)、超瑞利散射(HRS)等方法。但是，由实验得到的超极化率都是动态超极化率，需要通过相应的模型(如二能级模型)转换才能近似求得静态超极化率[5]；另一方面，实验中往往要利用共振增强效应，共振增强虽然使得超极化率大大增加，但是共振作用往往使参与作用的光场强度严重减弱以及光学材料的损耗增大[6]。研究证明，量子化学从头算方法对有机分子NLO系数计算能够取得很好的结果[7]。

理论上用量子化学研究非线性光学性质主要是态求和(SOS)方法，有限场(FF)方法和耦合微扰Hartree-Fock(CPHF)方法[8]。本文利用Gaussian03软件[9]的耦合微扰Hartree-Fock(CPHF)方法计算了体系的静态超极化率，另外利用CIS方法计算了体系的激发态，得到体系的优化构型、电荷分布、偶极距、前线分子轨道和吸收光谱等，从而深层次研究结构和非线性光学性质之间的关系。

1 理论方法

当分子受到激光照射时，分子在外场作用下强极化、产生诱导偶极子。在静态外场作用下，分子偶极矩μ可以唯象的展开成外电场E的泰勒级数[10]：

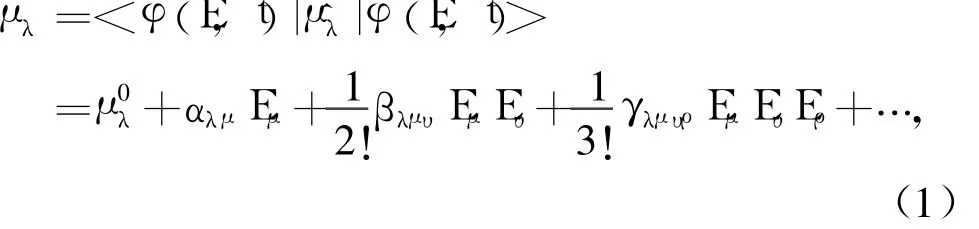
其中， λ， μ， ν和ρ表示直角坐标分量，例如x， y，z；μ， α， β和γ分别为无外场作用时的偶极矩、线性极化率、一阶超极化率和二阶超极化率。

在静态外场作用下，一阶超极化率β是分子偶极矩μ对于外电场E的二阶导数；又因为分子偶极矩μ是能量ε对于外电场E的一阶导数，所以一阶超极化率β是能量ε对于外电场E的导数，

因此，一阶超极化率β 的各个张量元可以表示为：

为了能跟实验值比较，可用式(3)和式(4)将β的各个张量元转化β的分量和标量值[11]：

2 结果与讨论

2.1 优化构型

本文在6-31G(d)基组水平上采用HF方法在气态条件下全优化吡啶盐衍生物分子阳离子，分别为4-(4-二甲基氨基-苯乙烯基)-N-甲基吡啶(R1)、2-(5-久洛尼啶)-亚乙烯基-N-甲基吡啶(R2)和4-[4-(N， N-二苯基)-苯乙烯基]-N-甲基吡啶(R3)，如图1所示。这三个分子具有相同的共轭桥π(乙烯基)和受体A(吡啶环)，唯一不同的只是给体D分别由三苯胺、久洛尼啶环、二甲基苯胺组成，属于典型的D-π-A型结构分子。频率计算后，发现没有虚频，说明得到的是基态稳定构型。计算结果显示， R1中氨基N原子上的两个甲基与分子骨架不在一个平面；R2通过两个六元环将给电子基团固定到苯环上，有效地提高了分子的平面性；R3中氨基N原子上两个苯环由于空间位阻作用而完全偏离分子平面，整个分子的平面性最差。但这些分子整体骨架结构呈良好的平面性，因此有利于分子内电荷的传递。

图1 吡啶衍生物分子结构

2.2 电荷分布与偶极矩

根据Mulliken电荷分布计算了体系的基态电荷分布qg、偶极矩μg和第一激发态电荷分布qe、偶极矩μe，表1列举的是各不同给体的电荷分布与偶极矩。由表1可以看出，与中性分子不同，这类离子性分子在基态具有更大的极性，表现在与激发态相比，基态具有更大的偶极矩，因此基态和激发态之间的偶极矩差为负值，预示了若在溶液中将随着溶剂极性的增强而逐渐使其吸收光谱蓝移。观察各给体基态电荷到激发态电荷改变Δqeg=qe-qg的大小，得到各给体的给电子能力大小次序为：三苯胺＞久洛尼啶环＞二甲基苯胺，这与各分子Δμeg=μe-μg的顺序一致，所以给体的给电子能力的强弱是决定Δμeg大小的主要因素。

表1 给体基态和激发态电荷分布(1.6022×10-19C)及偶极矩(Debye)

2.3 分子前线轨道

图2 给出了体系前线分子轨道分布情况，由图2可见，三个分子具有相似的HOMO和LUMO轨道电子云分布，分子的最高占据轨道(HOMO)电子云主要分布在三苯胺、久洛尼啶环、二甲基苯胺基团以及和其邻近的苯环上，最低空轨道(LUMO)的电子云主要分布在吡啶环以及和其邻近的苯环上，其他原子相对较少。电荷转移主要从电子给体(三苯胺、久洛尼啶环和二甲基苯胺和与其邻近的苯环)到电子受体(吡啶环和其邻近的苯环)。比较它们的前线分子轨道发现：随着给体的给电子能力的增强，电荷转移的能力也随之增强。

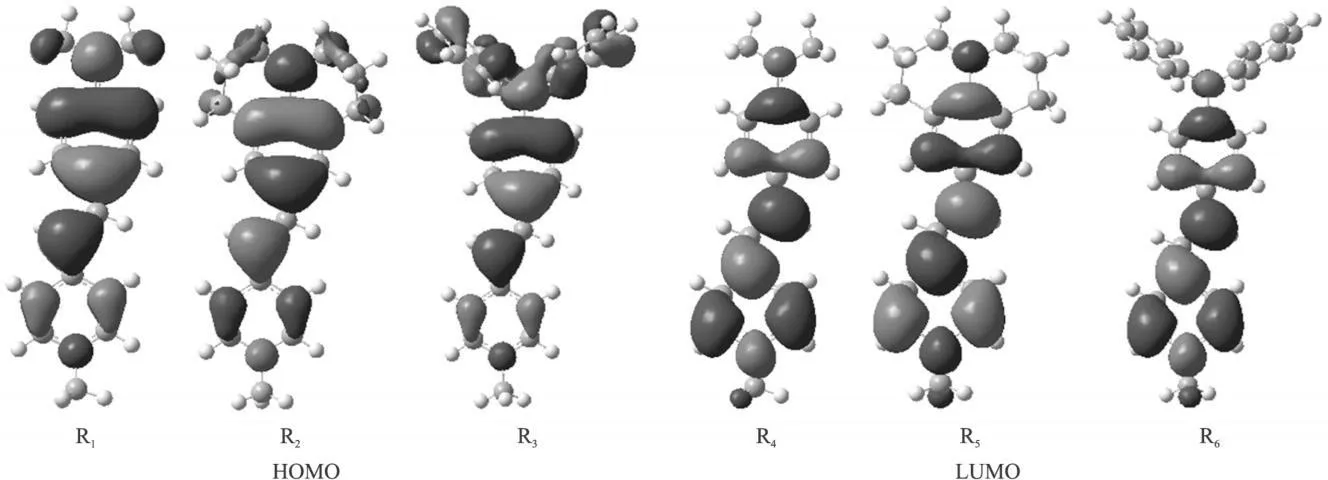
图2 分子前线轨道电子分布

表2列出了各个分子的前线分子轨道的能级分布情况，发现最高占据轨道(HOMO)和最低空轨道(LUMO)之间的能隙基本上是随给体的给电子能力的增强而减小。尽管三苯胺的给电子能力强于久洛定环，但是因为三苯胺上两个苯环偏离分子平面，阻碍了电荷从 HOMO到 LUMO的跃迁， 从而 R3的HOMO与LUMO之间的能隙相对R2增大。

表2 分子前线轨道的能级分布(eV)

2.4 光谱分析

在优化构型的基础上采用CIS方法计算分子的激发态，得到基态到各个激发态(选取第一激发态为例)的激发能、跃迁偶极距、最大吸收波长、振子强度和轨道成分，见表3。计算结果表明，所有分子的激发主要源于HOMO到LUMO轨道的跃迁，这个跃迁对最大吸收波长贡献最大，占80 %左右，第一激发态对分子体系非线性光学性质起决定作用，因此可借助二能级模型近似计算分子的一阶超极化率β。从分子R1到R3，第一激发态的振子强度和跃迁偶极矩逐渐增大，这是由给体的给电子能力的强弱决定的。另外，对于最大吸收波长，理论值和实验值相差很多，这主要是由CIS方法自身的限制导致，因为它未能考虑电子相关能，过高估计了分子的激发能，从而使吸收波长比实验值偏小，但是两者变化的趋势一致，因此在只需定性比较分子的某些性质时，可以认为这样的结果是可信的。

比较HOMO和LUMO之间的能隙与激发能发现：HOMO和LUMO之间的能隙越小， 则其激发能也越小。尽管三苯胺给电子能力强于久洛尼啶环，但是因R3中氨基N原子上的两个苯环发生空间位阻作用破坏了整个分子平面性，阻碍了电子从基态到激发态的跃迁，导致激发能比R2大，最大吸收波长较R2蓝移。因此，给体的给电子能力的强弱和分子平面性共同决定激发能大小。

表3 从基态到第一激发态的激发能ΔE(eV)、跃迁偶极矩μeg(Debye)、最大吸收波长λ(nm)、振子强度f及轨道成分

2.5 一阶超极化率

本文通过耦合微扰(CPHF)方法以及二能级模型(TEM)计算得到静态一阶超极化率β0和βTEM=，其中Δμeg为基态和激发态之间的偶极矩差， μeg为跃迁偶极矩， ΔE为从基态到激发态的激发能。表4给出了理论计算值，同时列出了在乙腈溶液中分别在1 300 nm和800 nm激发光源下用HRS方法测得的实验结果[13]。由于采用的从头计算方法未能充分考虑电子相关效应、基组效应、阴离子效应和溶剂效应等诸多因素的影响，所以计算值与实验值相差比较大，但两者表现的趋势一致，因此在结构类似体系的比较研究中，这些计算值是有效的[3]。

表4 静态一阶超极化率(10-30 esu)和βT0E M(10-30 esu)

表4 静态一阶超极化率(10-30 esu)和βT0E M(10-30 esu)

Δq βCPHF 0 βTEM 0 βExp.0(1300) βExp.0(800)R1 0.211978 159 -87.70 110±7 25±4 R2 0.220272 192 -102.63 220±17 76±5 R3 0.232390 219 -121.72

表4表明了这些静态一阶超极化率与给体的给电子能力之间的关系，虽然βCPHF0与βTEM0值(这里的负值由负的Δμeg引起)相差较大，但是它们都与给体的给电子能力成正比关系如图3(a)， 3(b)所示。这是因为给体的给电子能力与Δμeg(取绝对值)和μeg成正比关系如图3(c)， 3(d)所示，从而根据二能级模型可以推得给体的给电子能力与静态一阶超极化率成正比关系。

图3 给体的给电子能力Δq与βCPHF 0 、βTEM 0 、Δμeg、以及μeg的关系

3 结论

在HF/6-31G(d)水平上研究了吡啶盐衍生物分子的电子光谱和非线性光学性质。这类D-π-A型衍生物分子具有良好的分子平面骨架，有利于电荷在内传输。其中，三苯胺给电子能力最强，久洛尼啶环次之，二甲基苯胺最弱。这些给体的给电子能力与分子内电荷转移成正比关系。另外，给体的给电子能力还与跃迁偶极矩以及基态和激发态之间的偶极矩差成正比关系，从而使得给体的给电子能力与静态一阶超极化率成正比关系，对于此类分子二能级模型公式适用。尽管三苯胺给电子能力强于久洛定环，但是R3中氨基N原子上两个苯环由于空间位阻作用而偏离了分子平面，使得电荷转移能力减弱，因此激发能比R2大，最大吸收波长较R2蓝移。同样， R2的久洛尼啶环通过两个六元环将给电子基团固定到苯环上，有效地提高了整个分子的平面性，与R1比较，给电子能力大大增强，非线性活性显著增大。因此，通过对给电子基团空间结构的修饰，可以利用来优化分子的非线性效率。这些简单关系有助于我们深层次研究结构类似分子的结构与非线性光学性质之间的关系，从而为非线性材料的设计及合成提供理论帮助。

[ 1] Polymeric Materials and their Orientation Techniques for Second-Order Nonlinear Optics[ J] .Advances in Polymer Science，Vol.161.

[ 2] Recent Progress in Second-Order Nonlinear Optical Polymers and Dendrimers[ J] .Progress in Polymer Science， 2008， 33：1013-1058.

[ 3] 逯振平，韩奎，李海鹏， 张文涛， 黄志敏， 沈晓鹏.4-N-甲基苯乙烯砒啶盐衍生物非线性光学性质的理论研究[ J].原子与分子物理学报.2006， 23(5)：905-910.

[ 4] 吡啶盐二维电荷转移分子的设计-合成和超极化率的测定[J].化学学报， 2000， 58(4)：384-389.

[ 5] 李海鹏，韩奎，沈晓鹏，黄志敏， 王群.半花菁衍生物分子第一超极化率频率色散效应的理论研究[ J] .光学学报， 2005， 25(5)：655-660.

[ 6] 刘颂豪，赫光生.强光光学及其应用[ M] .第一版.广东：广东科技出版社， 1995.14-14.

[ 7] Talgat M.Inerbaev， Shigeki Saito， Rodion V.Belosludov.etc.Excited State Properties and Quadratic Optical Nonlinearities in Charged Organic Chromophores：Theoretical Analysis[ J] .The Journal of Chem ical Physics， 2006， 125：234702.

[ 8] 李海鹏，韩奎，逯振平，沈晓鹏，黄志敏， 张文涛，白磊.有机分子第一超极化率色散效应和双光子共振增强理论研究[ J] .物理学报， 2006， 55(4)：1827-1831.

[ 9] Frisch M J， et al.， Gaussian 03， Revision D.01[ sw] .Gaussian，Inc.， Wallingford CT， 2004.

[ 10] Julia E.Rice， Roger D.Amos， Susan M.Colwell， Nicholas C.Handy， Javier Sanz.Frequency-Dependent Hyperpolarizabilities with Application to Formaldehyde and Methyl Fluoride[ J].J.Chem.Phys， December 1990， 93(12)：8828-8839.

[ 11] 叶成， (法)习斯(Zyss， J).分子非线性光学的理论与实践[ M] .第一版.北京：化学工业出版社， 1996.94-101.

[ 12] 刘畅，黄维，吕昌贵， 崔一平.吡啶盐JVPI的合成及双光子吸收特性[C] //2008年东南大学校庆学术报告会.

[ 13] Benjamin J.Coe a， Simon P.Foxon a， Elizabeth C.etc.The Syntheses， Structures and Nonlinear Optical and Related Properties of Saltswith Julolidinyl Electron Donor Groups[ J].Dyesand Pigments 82(2009)171-186.