薄膜干涉光程差公式推导过程中的近似问题

王家慧 祁 铮 金钟辉

(中国农业大学应用物理系,北京 100083)

薄膜干涉光程差公式推导过程中的近似问题

王家慧 祁 铮 金钟辉

(中国农业大学应用物理系,北京 100083)

给出等倾干涉的光程差公式可推广至等厚干涉的证明.

等倾干涉;等厚干涉;光程差

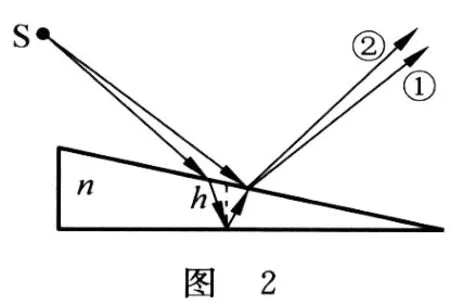
薄膜等倾干涉(图1)和等厚干涉(图2)中,经薄膜两个界面反射后的①、②两束光线之间的光程差(不计及半波损失)均为

但在许多教材[1～4]里仅对图1的薄膜等倾干涉的光程差公式作了详细的推导,得出式(1).然后只作粗略的说明,就将上述结论推广至图2所示的劈形膜的等厚干涉中,未作详细的推导.以下我们将作详细的推导.

先讨论一个平行薄膜,在图3所示情况下,计算两反射光线①、②之间的光程差(不计及半波损失).由于薄膜很薄以及通常观察条件下,可以认为图3中的 SD≈SA.即 SD-SA≪λ,其中λ为可见光波长.现在来估算,看看 SD-SA≪λ是否成立!

图3

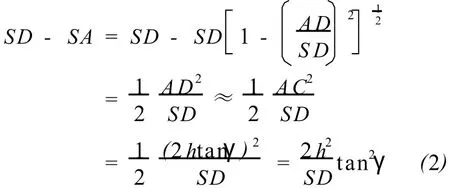
若 h=1.0μm,γ=5°,SD=0.4m,则

若 h=10μm,γ=45°,SD=0.4m,则

在SA≈SD情况下,我们采用许多教材中的方法,得出图3中的两反射光线的光程差为ΔL=2nhcosγ.

图4

再来讨论劈形薄膜的情况,如图4所示.图中CE平行于劈形膜的底面M N.在以上讨论中,我们已证明图4中的 SA≈SD,现在来证明图4中的 A E≪λ!

若α=1°,γ=5°,h=1μm,则

于是在 SA≈SD(即 SA-SD≪λ)和忽略 A E(即A E≪λ)的情况下,采用许多教材的方法,可得出图4中的两反射光线②、①之间的光程差为ΔL=2nhcosγ.

从以上讨论可以看出,将薄膜等倾干涉的光程差公式,直接推广至薄膜等厚干涉,从教学观点来看,是不够严谨的;在光程差的计算中采用近似要特别小心,因为我们处理的物理量可见光波长是一个很小的量.

[1] 金钟辉,梁德余.大学基础物理学[M].北京:科学出版社,2006.282～284

[2] 陆果.基础物理学[下][M].北京:高等教育出版社,1997.520

[3] 梁绍荣,管靖.基础物理学[上][M].北京:高等教育出版社,2002.243

[4] 赵凯华.新概念物理教程 光学 [M].北京:高等教育出版社,2004.117

2010-05-11)

中央高校基本科研业务费专项资助(2009-2-05).