中国期货价格期限结构模型实证分析

王 丽,王苏生,刘 艳,李志超

(哈尔滨工业大学 深圳研究生院,广东 深圳 518055)

一、引 言

期货价格的期限结构是指在某一时点,不同期限的期货价格与现货价格之间的关系.[1]由于期限结构的研究可以为投资决策和套期保值提供依据,因此引起学界的广泛关注.学者们从多个角度构建了不同的期货价格的期限模型,从最简单的单因素模型到复杂的三因素模型.

由于现货价格是期货价格的主要决定因素,大多数单因素模型选取现货价格为状态变量.Brennan和Schwartz[2]的单因素模型假设现货价格服从几何布朗运动,即dS=μSdt+σSdZ.但实证研究表明单因素模型的拟合能力较差.[3-4]为了更精确地描述商品价格的期限结构,有学者建立了二因素的期限结构模型.基于 Gibson和 Schwartz[5]的研究,Schwartz[3]以现货价格 S和便利收益δ为状态变量建立了二因素模型,假设便利收益δ服从均值回复过程,并作为随机红利影响现货价格的变动,使得现货价格具有均值回复的趋势,即dS=(μ-δ) dt+σSdZS,dδ=κ(α-δ)dt+σδdZδ.该模型在期货价格期限结构模型中影响力最广,很多更复杂的模型都是在该模型基础上改进提出的.[6-9]

早期关于商品价格期限结构研究中,都假设利率为常数,但这种假设不符合实际情况.[1]Schwartz[3]开创性地以现货价格、便利收益和利率为状态变量,提出了三因素模型,即 dS=(r-δ)dt+σSdZS,dδ=κδ(α-δ)dt+σδdZδ,dr=κr(m-r) dt+σrdZr.在该模型基础上,Casassus和 Collin-Dufresne[10]构建了三因素的仿射期限结构模型.实证结果表明,现货价格和便利收益的变化量为高度正相关.有学者提出质疑,假设两个高度相关的变量为随机变量是不合适的,模型不能解释每个状态变量的独自变化.[1]能否以不相关的状态变量建立期限结构模型呢?在这一背景下,Schwartz和Smith[4]建立了状态变量"正交"的二因素模型.该模型假设现货价格的对数lnSt可以分解为两个状态变量的和,即lnSt=χt+ξt.其中,短期偏离变量χt服从均值为零的均值回复过程,即dχt=-κ χtdt+σχdZχ,长期均衡变量ξt服从布朗运动,即 dξt=μdt+σξdZξ.Bernard等[11]实证结果表明,Schwartz和Smith模型对金属期货价格的拟合和预测能力较好.

鉴于目前国内尚无期货价格期限结构的实证研究,本文以2000-2008年的期铜价格面板数据为样本,考察中国期货价格的期限结构.在Schwartz和Smith[4]模型基础上,结合期货价格期限结构的实际情况,假设短期偏离变量和长期均衡变量服从均值回复过程,提出一个二因素的期货价格期限结构模型,以期对中国的期货价格进行较为准确的定价和预测.

二、期货价格期限结构模型

1.研究样本

按照《上海期货交易所结算细则》规定,期货合约均以当日结算价作为计算当日盈亏的依据,因此选取上海期货交易所(SHFE)期铜日结算价为研究样本.观测样本区间为2000年1月4日至2008年12月31日,共有2176个样本点.预测样本区间为2009年1月4日至2009年5月30日,共有96个样本点.考虑到数据的可获得性,兼顾交易价格的连续性,构造7个连续的期货合约,分别称之为 F1、F2、F3、F4、F5、F6和 F7,其中 F1是距离到期日最近的期货合约,F2是距离到期日第二近的期货合约,以此类推.其中,期铜日结算价的面板数据来自Wind数据库.2000-2008年的期货价格描述性统计结果如表1所示.

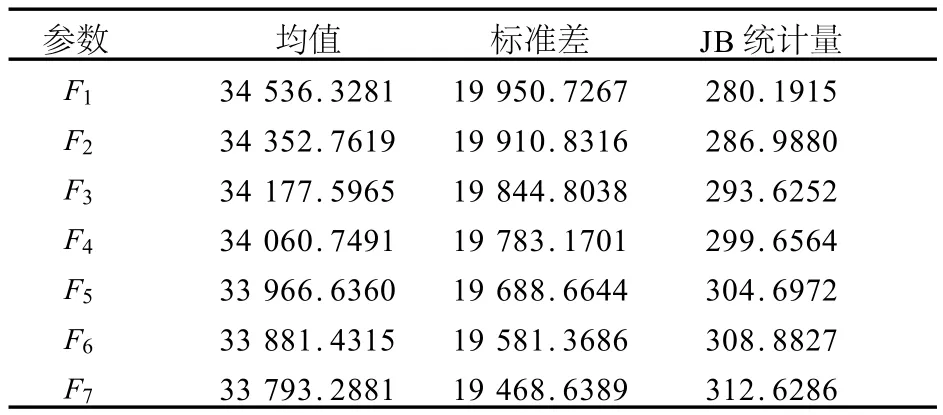
表1 描述性统计结果

均值统计量显示,近月合约价格大于远月合约价格,因此中国期铜的期限结构是现货升水(现货价格大于期货价格);JB统计量显示,期货价格时间序列不服从正态分布;标准差统计量显示,价格波动率随着到期期限增加而减少.

Bessembinder等[12]认为期货价格波动率是到期时间的减函数表明期货价格存在均值回复.Dai和Singleton[13]指出,均值回复速度κ在利率期限结构模型中具有重要的作用,随着到期期限 T的增加,κ的影响作用趋于零,而且κ越大衰变越快,所以较大的κ表示影响时间较短的因素的均值回复速度.因为期货价格期限结构与利率期限结构类似,Dai和Singleton的观点同样适用于期货价格期限结构模型.在均值回复情况下,当到期期限较短时,多种因素共同影响期货价格;当到期期限较长时,只有长期因素影响价格.随着到期期限增加,引起期货价格改变的因素变少,故期货价格波动率是到期期限的减函数.基于上述理论分析,本文假设影响期货价格变动的因素服从均值回复过程,但Schwartz和Smith[4]假设长期均衡变量服从布朗过程.本文第四部分将采用多种误差统计量,实证说明本文提出的模型比Schwartz和Smith模型能更准确地描述期货价格的期限结构.

2.期货价格期限结构模型

设现货价格的对数可以分解成短期偏离和长期均衡两部分

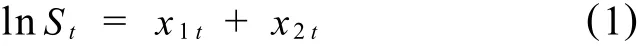
式中:St表示现货价格;x1t表示价格的短期偏离; x2t表示长期均衡价格.假设短期偏离变量服从均值为零的均值回复过程,长期均衡变量服从均值为常数的均值回复过程

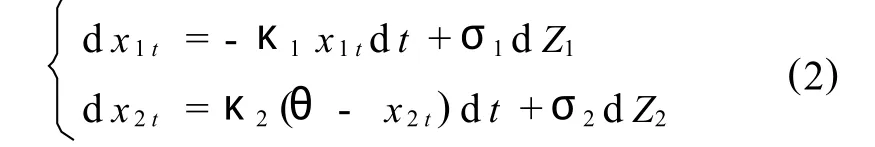
式中:κ1表示短期偏离的均值回复速度;σ1表示短期偏离的波动率;dZ1表示短期偏离的标准布朗运动的增量;κ2表示长期均衡的均值回复速度;θ表示回复的均值;σ2表示长期均衡的波动率;dZ2表示长期均衡的标准布朗运动的增量,且dZ1dZ2=ρ12dt.

短期偏离变量的改变量反映短期因素如天气变化和供应中断等引起的价格变化.这些因素不会长期存在,因此假设该变量服从均值为零的回复过程.长期均衡变量改变量反映通货膨胀、政治和规章制度等长期因素的影响引起的价格变化.这些因素长期存在,导致价格维持在某一水平,因此假设该变量服从均值为常数的均值回复过程.虽然这两个状态变量不能直接观测,但较长到期时间的期货合约价格提供均衡变量的信息,短期与长期期货合约的价格差提供短期偏离的信息.

期货价格等于到期时风险中性测度下的现货价格期望[3],即 F(0,T)= E*(ST),因此为求出正确的期货价格表达式,在式(2)中加入风险溢价因子

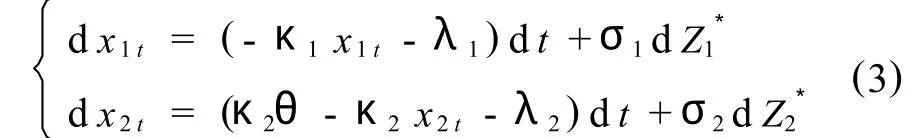
式中:λ1表示短期风险溢价因子;dZ表示风险中性测度下的短期偏离变量的标准布朗运动的增量; λ2表示长期风险溢价因子;dZ表示风险中性测度下的长期均衡变量的标准布朗运动的增量,且=ρdt.12

若给定状态变量初值 x10和 x20,可得状态变量的期望和协方差矩阵

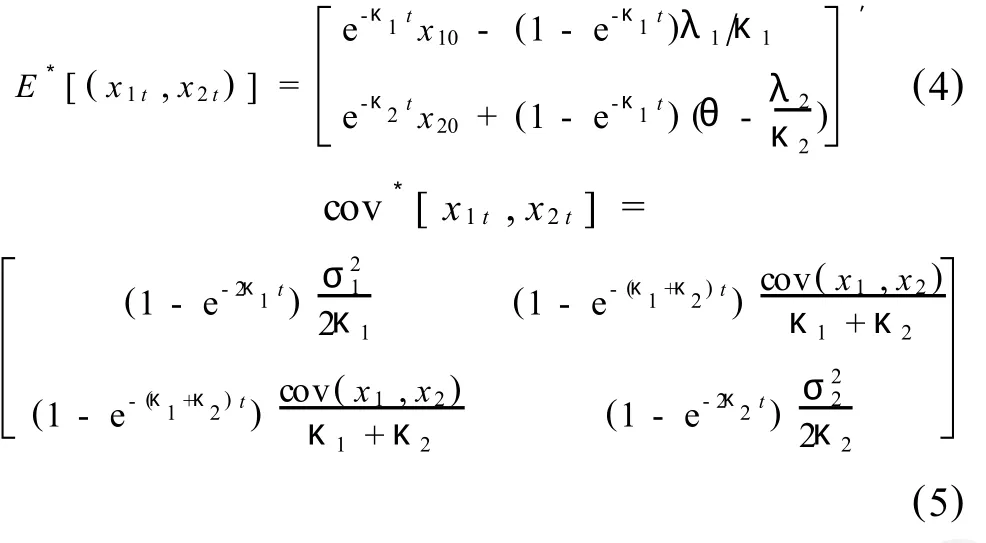
则根据式(1),得到lnSt的期望和方差

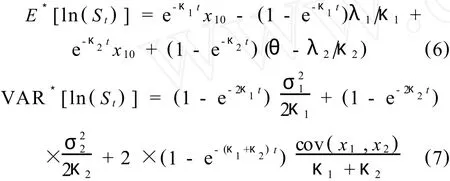
由正态分布的特性可得

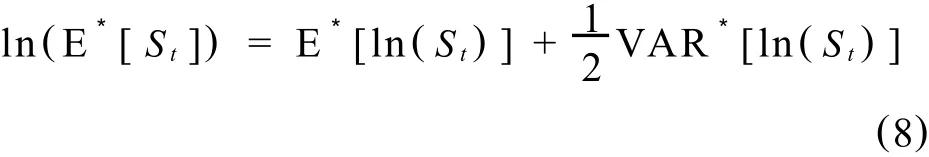
将式(6)、(7)带入式(8),得到期货价格模型

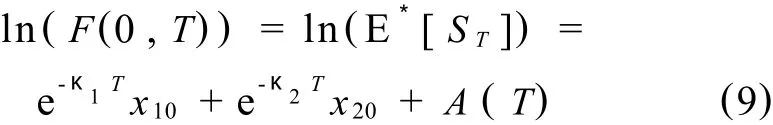
其中:

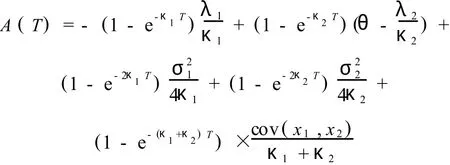
则在时刻t,到期时间为 T的期货合约F(t,T)的价格模型为

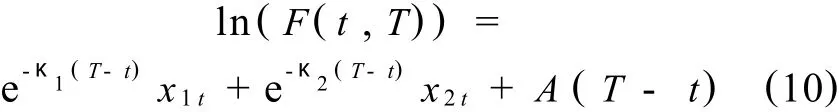
三、研究方法和实证分析

1.卡尔曼滤波

卡尔曼滤波由一系列递归数学公式描述,其中量测方程描述可观测的期货价格与不可观测的状态变量之间的关系,转移方程描述状态变量的更新过程.卡尔曼滤波的功能强大,通过可观测数据它不仅可以估计模型隐含的状态变量,还可以结合极大似然法求得模型的未知参数.[3]

根据式(10),模型的量测方程为

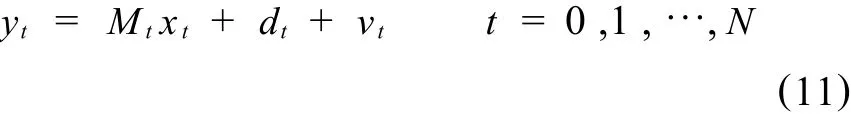
式中:yt=[lnF(Ti)]是时刻t,到期时间为 Ti的期货价格对数的 HX1向量(i=1,2,…,H);Mt= [exp(-κ1Ti)exp(-κ2Ti)]是 HX2向量;dt= [A(Ti)]是 HX1向量;vt是序列不相关的HX1向量,且E[vt]=0,cov[vt]=Vt.

根据式(2),模型的转移方程为

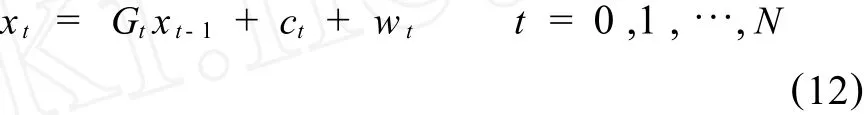
2.参数估计

选取具有代表性的3个期货合约:到期时间最短的F1,到期时间最长的F7和到期时间居中的F4,采用Eviews 5.0统计软件对 F1、F4和 F7进行数据处理,运用卡尔曼滤波和极大似然法,即可求得模型的未知参数和隐含状态变量值.[14]参数估计结果如表2所示.

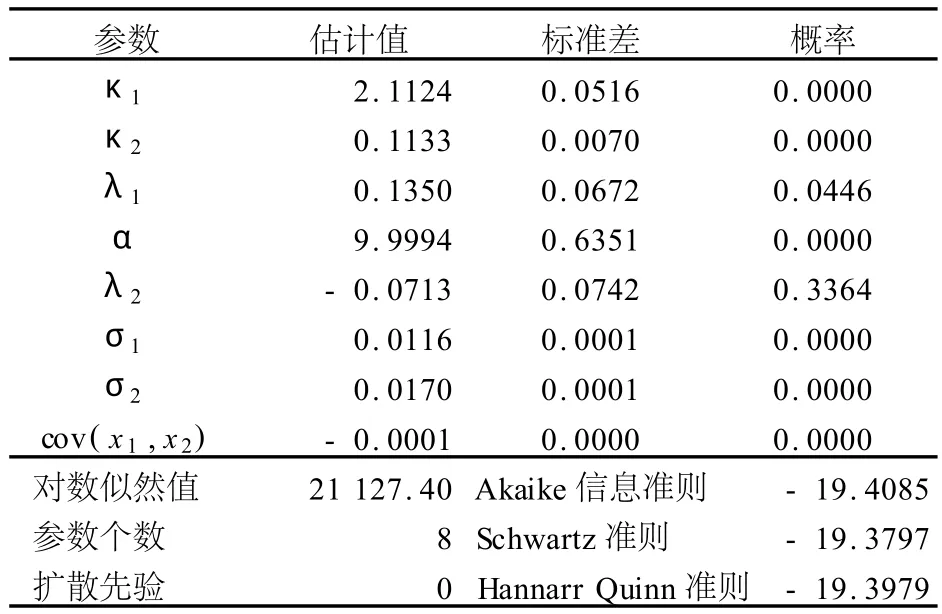
表2 参数估计结果

从表2可以看出,短期和长期均值回复参数κ1和κ2都显著不为零,说明短期和长期偏离变量服从均值回复过程.短期和长期风险溢价因子λ1和λ2在1%水平下不显著,这一结果和文献[3]、[4]结果一致.因为均值回复速度κ越大衰变越快,影响价格变动的持续时间越短,因此本文的短期偏离的均值回复速度κ1大于长期均衡的均值回复速度κ2,符合最初模型假设.由于中国期铜市场的期货合约到期期限都不超过1年,因此中国期铜的价格同时受短期因素和长期因素的制约.状态变量增量的协方差表明短期与长期增量负相关.

四、模型能力比较

1.模型能力评价标准

在求得模型参数和状态变量后,利用式(10)即可求得拟合的期货价格对数值,拟合值与真实值的差即为模型的拟合误差.采用平均绝对误差(MAE)和误差均方根(RMSE)统计量,评价模型的拟合和预测能力.

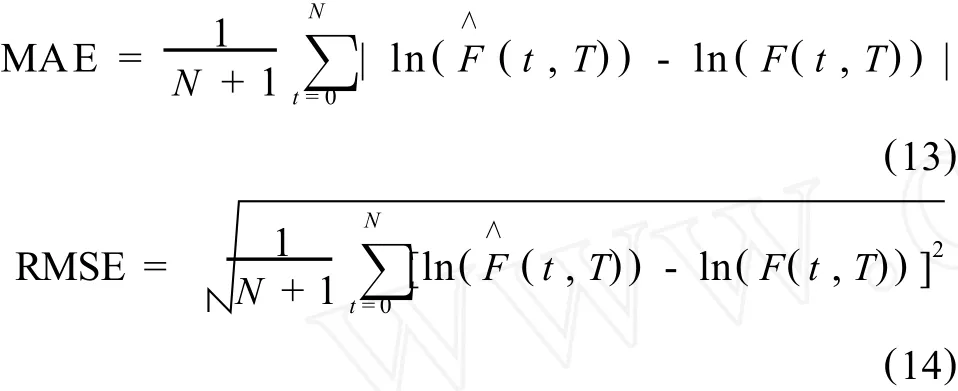
2.模型拟合能力比较

拟合误差统计量如表3所示.从表3可以看出, Schwartz和Smith[4]的模型(简称模型1)的MAE和RMSE值大于本文提出的二因素模型(简称模型2)的MAE和RMSE值,说明模型2的拟合能力优于模型1.虽然模型的参数和状态变量是用 F1、F4和 F7这3个期货合约数据得到的,但是模型对观测期内的其他期货合约(F2、F3等)的拟合能力也较好,说明 F1、F4和 F7这3个期货合约具有代表性,可较好地估计模型参数.

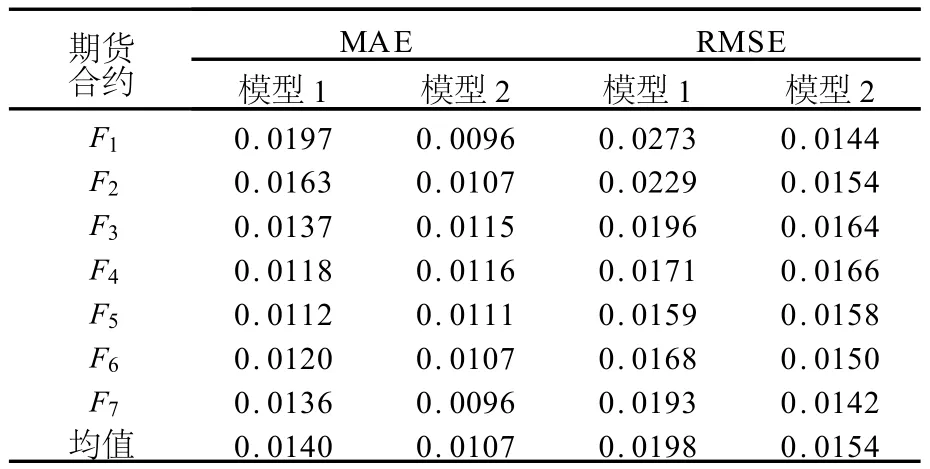
表3 拟合误差统计量

3.模型预测能力比较

以上是评价模型对观测样本数据的拟合能力,下面考察模型对观测期外样本的预测能力,采用递归方式不断更新模型的参数值,以提高模型的预测精度.[11]

预测误差统计量如表4所示.MAE和RMSE的比较结果显示,模型2的预测误差小于模型1,这说明模型2的预测能力优于模型1.

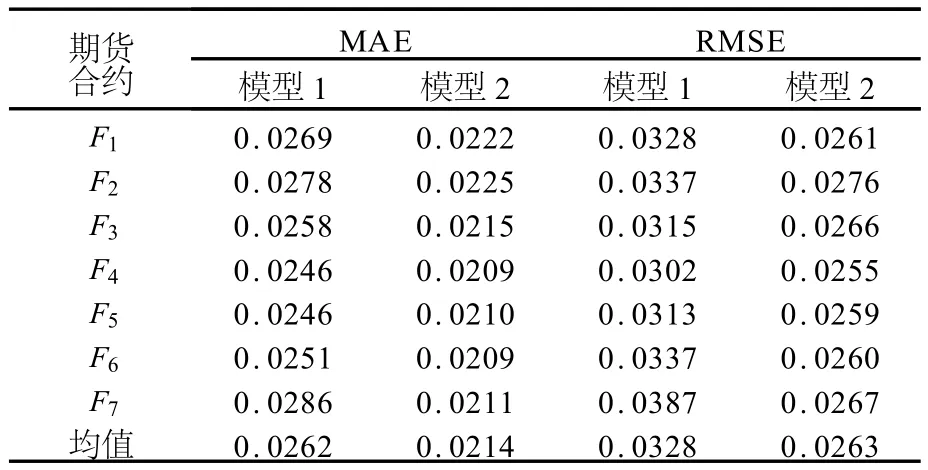
表4 预测误差统计量

五、结 语

本文以短期偏离和长期均衡为状态变量,构建一个期货价格期限结构的二因素模型,以2000-2008年的期铜价格面板数据为研究样本,研究中国期铜价格的期限结构,并运用卡尔曼滤波和极大似然法进行实证分析.研究结果表明,中国期铜价格受短期和长期因素的共同作用,到期期限越短,受短期因素影响越大,波动率越大.与 Schwartz和Smith[4]的模型相比,本文提出的模型总体上更好地刻画了中国期铜价格的行为特征,具有更好的拟合与预测能力.同时,本研究对期货投资决策和套期保值具有一定的指导意义.

[1]LAUTIER D.Term structure models of commodity prices: a review[J].Journal of Alternative Investments,2005,8 (1):42-63.

[2]BRENNAN M J,SCHWARTZ E S.Evaluating natural resource investments[J].Journal of Business,1985,58(2): 135-157.

[3]SCHWARTZ E S.The stochastic behavior of commodity prices:implications for valuation and hedging[J].Journal of Finance,1997,52(3):923-973.

[4]SCHWARTZ E S,SMITH J E.Short-term variations and long-term dynamics in commodity prices[J].Management Science,2000,46(7):893-911.

[5]GIBSON R,SCHWARTZ E S.Stochastic convenience yield and the pricing of oil contingent claims[J].Journal of Finance,1990,45(3):959-975.

[6]HILLIARD J E,REIS J.Valuation of commodity futures and options under stochastic convenience yield,interest rates,and jump diffusions in the spot[J].Journal of Financial and Quantitative Analysis,1998,33(1):61-86.

[7]SCHWARTZ E S.Valuing long-term commodity assets [J].Journal of Financial Management Association,1998, 27(1):57-66.

[8]NEUBERGER A.Hedging long-term exposures with multiple short-term futures contracts[J].Review of Financial Studies,1999,12(3):429-459.

[9]VELD-MERKOULOVA Y V,DE ROON F A.Hedging long-term commodity risk[J].Journal of Futures Markets, 2003,23(2):109-133.

[10]CASASSUS J P,COLLIN-DUFRESNE P.Stochastic convenience yield implied from commodity futures and interest rates[J].Journal of Finance,2005,60(5):2283-2331.

[11]BERNARD D J,KHALALF L,KICHIAN M,et al. Forecasting commodity prices:GARCH,jumps,and mean reversion[J].Journal of Forecasting,2008,27(4): 279-291.

[12]BESSEMBINDER H,COUGHENOUR J F,SEGUIN P J,et al.Mean reversion in equilibrium asset prices:evidence from the futures term structure[J].Journal of Finance,1995,50(1):361-375.

[13]DAI Q,SINGLETON KJ.Specification analysis of affine term structure Models[J].Journal of Finance,2000,55 (5):1943-1977.

[14]高铁梅.计量经济分析方法与建模:Eviews应用及实例[M].北京:清华大学出版社,2006:353-385.