基于联系数的直觉模糊多属性决策不确定分析与应用
王 霞,贾学龙
(天津科技大学理学院,天津 300457)
保加利亚学者Atanassov于1983年提出了直觉模糊集的概念,模糊集的特点是能够同时考虑元素与给定集合的隶属度、非隶属度和犹豫度,从而能比Zadeh给出的经典模糊集更细致地刻画研究对象的模糊性[1–2].
1993年,Gau等[3]又提出 Vague集的概念,但Bustiuce和Burillo[4]于1996年指出,Vague集实质上仍然是直觉模糊集.1994年 Chen和 Tan[5]将 Vague集应用于模糊多指标决策问题,2000年 Hong和Choi[6]在 Chen工作的基础上又提出精确函数应用于多目标决策.国内学者徐泽水[7]、南江霞等[8]和黎华等[9]也先后把直觉模糊集用于多属性决策,但这些工作的一个明显不足是:忽略了对直觉模糊集中犹豫度所承载的不确定性分析,使得在客观意义上具有不确定性的直觉模糊集多属性决策问题变成完全确定的决策问题,从而使决策结果失去了理论价值和实际意义.
本文考虑二元联系数与同异反联系数的等价性,把直觉模糊数直接转换成二元联系数,利用二元联系数的普通加、乘运算进行直觉模糊决策,利用二元联系数i的不同取值考察不确定性对直觉模糊决策的影响,并结合一个实例说明具体的计算过程,从而为直觉模糊多属性决策提供了一种新的简便算法.
1 直觉模糊数及其向二元联系数的转换
1.1 直觉模糊数
定义1 设X是一个非空集合,界定形如
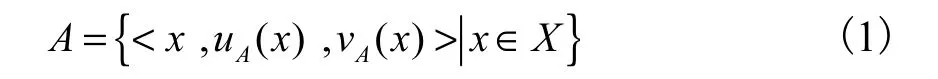
的三重(元)组称为X上的一个直觉模糊集,其中uA: X →[0,1] ,vA: X→[0,1]均为X上的普通模糊集,这里 uA(x) ,vA(x)分别表示X上的元素x属于A的隶属度和非隶属度,并满足0 ≤uA(x) +vA(x )≤ 1,∀x∈X 用IFS[X]表示X上的所有直觉模糊集全体构成的集合.
进一步,称
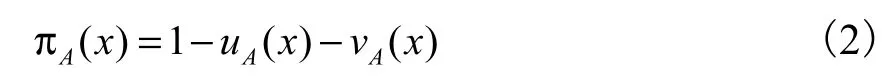
为X中元素x属于A的犹豫度,也称为直觉模糊集A的直觉指标[10].
易知,0≤πA(x)≤1,∀x∈X,特别地,若πA(x)=0,则直觉模糊集退化为Zadeh的模糊集.称数对(uA(x),vA(x))(x∈X )为直觉模糊数[11].由文献[5]知,通常把直觉模糊数的一般形式简记为 α=,其中0 ≤ uα+vα≤ 1,并定义得分函数s(α)=等.
1.2 直觉模糊数转换成二元联系数
由直觉模糊集的定义,把直觉模糊集A可以等价地写成
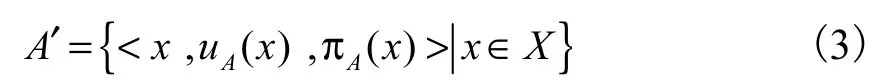
由于隶属度和非隶属度是对事物的肯定性与否定性的回答,具有确定性,犹豫度是对事物排除隶属度和非隶属度后的一种刻画,具有不确定性,将直觉模糊数的隶属度uA(x)与联系数的同一关系a相对应,犹豫度πA(x)与联系数的差异关系b相对应,直觉模糊数就转化为二元联系数.即令uA(x)=a和πA(x)=b ,则直觉模糊数(uA(x),πA(x))(x∈X)就 可以写成二元联系数

称式(4)为直觉模糊数向集对分析的二元联系数的转换形式.由式(4)看出,直觉模糊数中的隶属度与犹豫度的数值在转换前后没有改变,所不同的是,犹豫度 πA(x)在转换后,按联系数的定义,被添置了一个不确定系数i,而正是这个i,把直觉模糊数与联系数μ(x)显著地区别开来;其次是在二元联系数中,原直觉模糊数中的隶属度uA(x)与犹豫度πA(x)用“+”系,成为一代数式,从而为后续的代数运算提供了客观条件.
2 多属性决策
2.1 问题描述
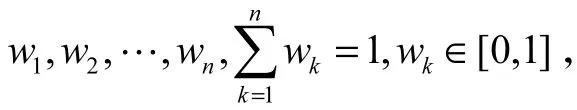
2.2 决策步骤
步骤1:把所给的各指标的直觉模糊数αtk=(utk,vtk)改写成特别,当各指标权重wk是用非定量信息表示时,用文献[12]的方法,将各wk也改写成二元联系数μwk的形式.
步骤2:利用式(4)把各αt′k转化成二元联系数μtk(x)=atk+btki .
步骤3:建立综合加权模型

或

步骤 4:对 M (st)作不确定性分析,也就是对其中的i作取值分析,由于权重不能为负,所以,一般让i在[0,1]区间等间隔取值,如令 i= 0,0.5,1等.根据M (st)的大小作出优劣排序,M (st)大的优先于M (st)小的.同时考察 M (st)在不同i值下的大小变化及其带来的排序变化.必要时,从数学期望的角度计算各方案的平均序数值p,p值小的方案被认为是数学期望意义上最优方案.
3 应用实例
为便于比较和分析,采用文献[7]中的例子说明本方法的具体应用.
一个家庭欲购买一台冰箱,现有 5种品牌st(t = 1,2,…… ,5)可供选择,主要的评价指标(属性)有Gk(k = 1,2,……,6)共 6项,其中G1表示“安全性”,G2表示“制冷性”,G3表示“结构性”,G4表示“可靠性”,G5表示“经济性”,G6表示“美观性”.利用统计方法,得到方案 st(t = 1,2,……,5)对属性 Gk(k=1,2,……,6)的满意程度utk和不满意程度vtk,记直觉模糊数为 αtk= (utk,vtk),见表1.
已知各指标的权重信息wk如下:w1≤0.3,w2≤ 0.2,0 .2 ≤ w3≤ 0.5,w4≤0.1,0 .1 ≤w5≤0.4,w6≥ 0.2,试作出决策.
步骤 1:将表 1利用式(4)改写成用二元联系数表示的决策矩阵表,见表2.

表1 直觉模糊决策矩阵表Tab.1 Intuitionistic fuzzy decision matrix

表2 权重和指标值转换为二元联系数的直觉模糊决策矩阵表Tab.2 Intuitionistic fuzzy decision matrix of binary connection number by weight and target value
步骤2:应用式(5)计算各方案的综合加权联系数st,得表3.

表3 各方案综合加权联系数stTab.3 Varied program synthesize weigh connection number st
步骤3:计算和分析 M (st)在不确定性下的各种方案排序,得表4.
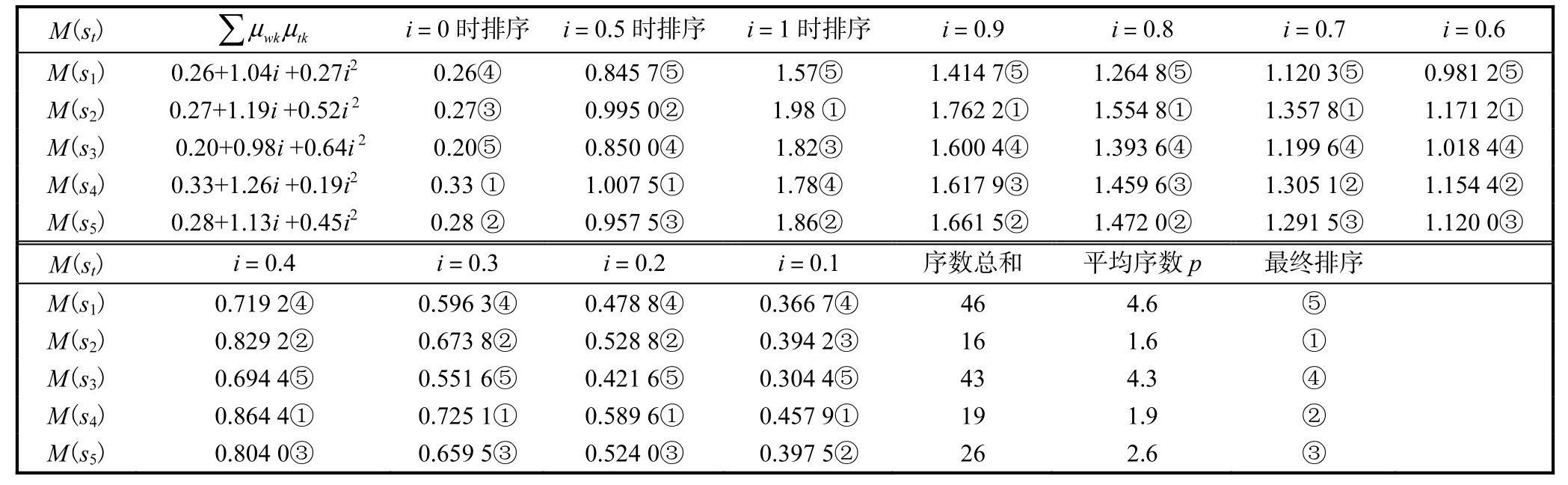
表4 i取不同值时M(st)的排序Tab.4 M(st)’ s rank of different value of i
由表 4、可见,在忽略不计不确定性条件下,是s4优于s5优于s2优于s1优于s3,当考虑不确定性,仅取i= 0.5,i=1这两种情况时,除s1仍为最差方案外,其余 4个方案的优劣顺序在i=0.5时与i=1时都不同.由于i在[0,1]区间,取i=0时相当于忽略不确定性,因而又作了 i= 0.1,0.2,? ,1共 10种情况下的M (st)计算,并作各方案的序数总平均p处理,结果是s2优于s4优于s5优于s3优于s1,这一结果与文献[7]中的排序结果完全一致.但文献[7]是在经过一系列繁琐计算后得到的结果,没有作不确定性分析.
本文是在承认不确定性条件下,用联系数客观地描述这些不确定性,通过联系数的普通加、乘运算及不确定性分析得到的结果,整个分析计算过程简单,且原理清晰.
[1] Atanassov K T. Intuitionistic fuzzy set [J]. Fuzzy Sets and Systems,1986,20(1):87-96.
[2] Zadeh L A. Fuzzy sets [J]. Inform and Control,1965,8(3):338-353.
[3] Gau W L,Buehrer D J. Vague sets[J]. IEEE Transactionson Systems,Man,and Cybernetics,1993,23(2):610-614.
[4] Bustince H,Burillo P. Vague sets are Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1996,79(3):403-405.
[5] Chen S M,Tan J M. Handling multicriteria fuzzy decisiorr making problems based on vague set theory[J]. Fuzzy Sets and Systms,1994,67(2):163-172.
[6] Hong D H,Choi C H. Multicriteria fuzzy decision-making problems based on vague set theory [J]. Fuzzy Sets and Systems,2000,114(1):103-113.
[7] 徐泽水. 直觉模糊偏好信息下的多属性决策途径[J].系统工程理论与实践,2007,27(11):62-71.
[8] 南江霞,李登峰,张茂军. 直觉模糊多属性决策的Topsis法[J]. 运筹与管理,2008,17(3):38-41.
[9] 黎华,王周敬. 基于直觉模糊集的多属性决策问题[J].昆明理工大学学报:理工版,2008,33(6):109-112.
[10]Szmidt E,Kacprzyk J. A consensus reaching process under intuitionistic fuzzy preference relations[J].International Journal of Intelligent Systems,2003,18(7):837-852.
[11]刘秀梅. 基于联系数的直觉模糊数多指标评价研究[J].连云港师范高等专科学校学报,2008(4):91-94.
[12]刘秀梅,赵克勤. 基于区间数确定性相互作用点的多属性决策[J]. 数学的实践与认识,2009,39(8):68-75.

