线性混合模型中参数估计的容许性

薛 蕊，郭大伟

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)

0 引 言

含有两个方差分量的线性混合模型包括单向分类随机效应模型，两向分类无交互效应的混合模型以及Panel模型中的单向误差分类回归模型等，它广泛地应用于生物、经济、医药等领域的数据分析中，所以对这种模型的研究在线性混合模型中占有重要的地位.这种模型的一般形式为

y=Xβ+Uξ+ε，

(1)

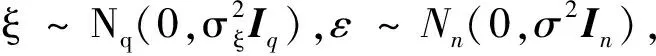
对于固定效应β，已有文献多从无偏性和容许性这两方面进行讨论，本文在第2节给出了β的线性可估函数Sβ的一个线性无偏估计类，在二次损失下通过讨论该类中Sβ的线性无偏估计不可容许的充分条件，进而得到可容许的必要条件.

在此采用A′,rank(A),tr(A),μ(A)分别表示A的转置，秩，迹和A的列向量张成的子空间.

1 方差分量估计的容许性及ANOVA估计的改进

取矩阵H(n-r)×n满足条件：HX=0,HH′=In-r，用H左乘模型(1),令z=Hy，得到新模型

z=HUξ+Hε，

(2)

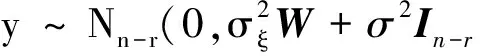
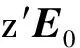
(3)

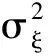
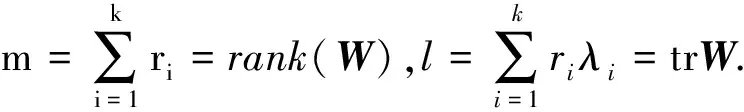
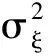
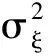
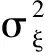
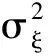
(4)

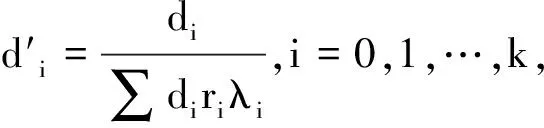
下面考察c1,c2,c12对d0的单调性，令它们分别对d0求偏导数，得

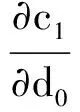
(5)

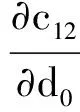
(6)

进一步为了得到c1,c2,c12对di,i=1,2,…,k的单调性，令它们分别对di求偏导数:

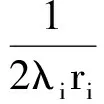
(7)

(8)

(9)

注意到：若式(7)大于0，则diλi>0，那么必有式(8)和式(9)大于0，即如果c1是di的增函数，那么c2,c12也是di的增函数，这时若减少di的值会同时减小c1,c2,c12的值，所以估计是不容许的.

至此，在∑diri≥0的前提条件下，推导出L1中可容许估计所要满足的条件.而当∑diri<0时，情况就变得较为复杂，没有确定的结论.文献[3]的证明中没有考虑到这一点.于是在此将估计类L1改进为

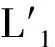
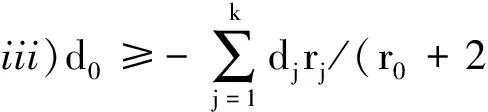
2 固定效应β的线性可估函数Sβ的可容许性

在模型(1)下讨论固定效应β的线性可估函数Sβ的线性无偏估计在二次损失下的可容许性，这里S为已知的t×p阶矩阵，那么存在一个n×t阶矩阵B，使得S=B′X.考虑Sβ的一个线性无偏估计类

L2={φT=(SX++TH)y:T为任意t×(n-r)阶矩阵}，

这里H同模型(2)中的H.

R(φT)=E[((SX++TH)y-Sβ)′((SX++TH)y-Sβ)]=

tr[(SX++TH)′(SX++TH)∑(θ)]=

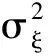
(10)

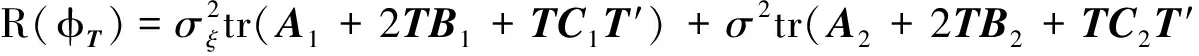
φT在L2中不可容许定义为∃φT1∈L2使得R(φT)≥R(φT1)，即

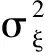
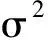
(11)

定理2对于模型(1)，Sβ的线性无偏估计φT不可容许的充分条件是存在t×(n-r)阶矩阵Q使得

trQ(Bi+CiT′)>0,i=1,2.

(12)

证明设Q使得式(12)成立，则必有Q≠0，取T1=T-εQ,ε>0，则

tr(T-T1)(Bi+CiT′)-tr(T-T1)Ci(T-T1)′=
2εtrQ(Bi+CiT′)-ε2trQCiQ′=ε[2trQ(Bi+CiT′)-εtrQCiQ′]，

当ε充分小时，上式大于0对i=1,2都成立，于是由式(11)可知φT是不容许的.

为叙述方便，定义p·q维向量v=Vec(Q′)，bi(T)=Vec(Bi+CiT′)，i=1,2，这里Vec(M)是指将矩阵M按列拉直.于是式(12)可表示为v与bi(T)的内积

(v,bi(T))>0.

(13)

定理3在模型(1)中Sβ的线性无偏估计φT可容许的必要条件是：存在a1,a2≥0,a1+a2>0，使得

a1b1(T)+a2b2(T)=0.

证明设φT可容许，若对任意的a1,a2≥0且a1+a2>0，a1b1(T)+a2b2(T)≠0，则b1(T),b2(T)生成的凸包不包含o点，由凸集分离定理知，存在一个Rt·(n-r)中过o点的超平面π，使由b1(T),b2(T)生成的凸包在π的一侧，由此可知存在π的一个法向量v使得式(13)成立，从而由定理2知φT是不容许的，矛盾.定理得证.

[1] 王松桂.线性模型的理论及应用[M].合肥：安徽教育出版社，1987.

[2] 王松桂，尹素菊.线性混合模型参数的一种新估计[J].中国科学A辑,2002,32(5):434-443.

[3] 范永辉,王松桂.混合模型中方差分量估计的容许性及非负估计[J].应用概率统计,2008,24(4):354-360.

[4] Tatsuya K. Estimation of variance components in mixed linear models[J]. Journal of Multivariate Analysis,1995,53:210-236.