GOM(1,1)模型背景值构造的重新改进

陈鹏宇

灰色预测模型是灰色理论的重要组成部分，而GM(1,1)模型是灰色预测模型中最基本的预测模型，已经在许多领域得到了广泛应用[1-3].传统GM(1,1)模型以正向累加生成为基础，相对于正向累加生成，一种反向累加生成定义被提出.灰色GOM(1,1)模型正是基于反向累加生成得出的一种灰色预测模型[4-5].杨知等[6]分析反向累加生成的特点，并从背景值的几何意义出发，对GOM(1,1)模型进行了改进.文献[6]中虽然认识到了GOM(1,1)模型的缺陷，但却忽略了改进背景值的建模适应性问题，该文仍从文献[6]中提到的背景值几何意义出发，分析文献[6]中改进背景值形式的不足，建立新的具有更强建模适应性的背景值形式.

1 反向累加生成及GOM(1,1)模型

其累减还原序列为

GOM(1,1)模型白化方程为

(1)

其中a为发展系数，b为灰作用量，是微分方程的参数.

灰微分方程为

-x(0)(k-1)+az(1)(k)=b，k=2，3，…，n.

(2)

文献[6]中应用齐次指数序列在区间[k-1,k]上的积分作为背景值，推导出了GOM(1,1)模型改进的背景值形式:

(3)

GOM(1,1)白化型响应式为

(4)

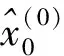
参数计算[ab]T=(BTB)-1BTY,其中

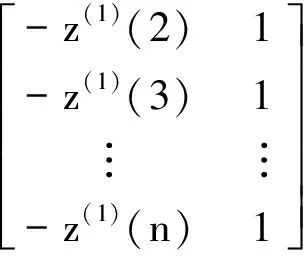
2 GOM(1,1)模型的改进

下面以GM(1,1)模型缺陷分析理论中最常用的背景值几何意义分析来说明GOM(1,1)模型的缺陷并对其进行改进.

即

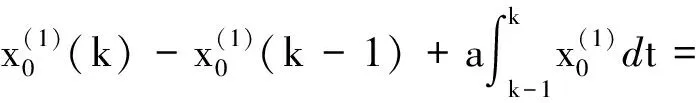
(5)

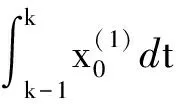
文献[6]中以齐次指数序列在区间[k-1,k]上的积分作为背景值，推导出了新的背景值形式.该改进背景值形式存在两个问题：首先，其是基于累加序列为齐次指数序列推导出的，而文献[7]中已经指出当原始数据为齐次指数序列时，其一次累加序列为非齐次指数序列，根据文献[7]的思想，则以非齐次指数序列在区间[k-1,k]上积分得到的背景值形式更能符合实际发展，从文献[6]中的齐次指数序列拟合实例也可以看出，其并不能完全拟合齐次指数序列.其次，即使是背景值形式以非齐次指数序列积分得到，虽然能完全拟合齐次指数序列，但其并不一定能适应于近似指数序列建模，这个问题将在文后指出.

下面建立一种既能满足白指数律，又能适应于近似指数序列建模的背景值形式，对于利用几何思想改进的背景值形式，可以利用文献[8]中的，而不必进行复杂的积分计算，文献[8]中的背景值形式为

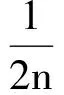
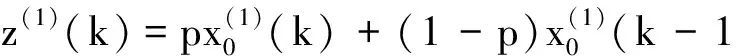
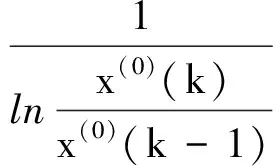
文献[8]在推导出该背景值构造形式时是基于两点间的面积不同得出的，而当原始数据为近似齐次指数序列时，每两点间满足面积相等的n或p值当然并不一样，这便是前文指出的近似指数序列拟合时的问题，显然以近似指数序列建模时，利用积分思想的所有推导全部不会成立，故以齐次指数序列或者非齐次指数序列推导出的背景值形式都不适合于近似指数序列建模.因此该文建立了变权背景值构造形式，即

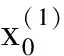
只要求出每两点间满足面积相等的pk值即可以解决近似齐次指数序列下的背景值缺陷问题.

至于权值pk求解问题，在此采用具有全局寻优能力的非线性搜索算法-模式搜索法.具体操作可利用Matlab编程及其模式搜索法工具箱，以pk=0.5为初始值，原始数据残差平方和最小的目标下搜索最佳背景值权值.

3 实例比较

仍然采用文献[6]中的实例建立本文的改进模型，并与文献[6]中改进模型以及普通GOM(1,1)模型(背景值为相邻累加值的均值)进行比较.

例12000-2004年全国造林总面积中所造经济林面积的原始序列，见表1.

表1 原始数据

以上述数据建立普通GOM(1,1)模型、改进GOM(1,1)模型以及文献[6]中GOM(1,1)模型，并求出相应的时间响应式.

各模型预测结果见表2.

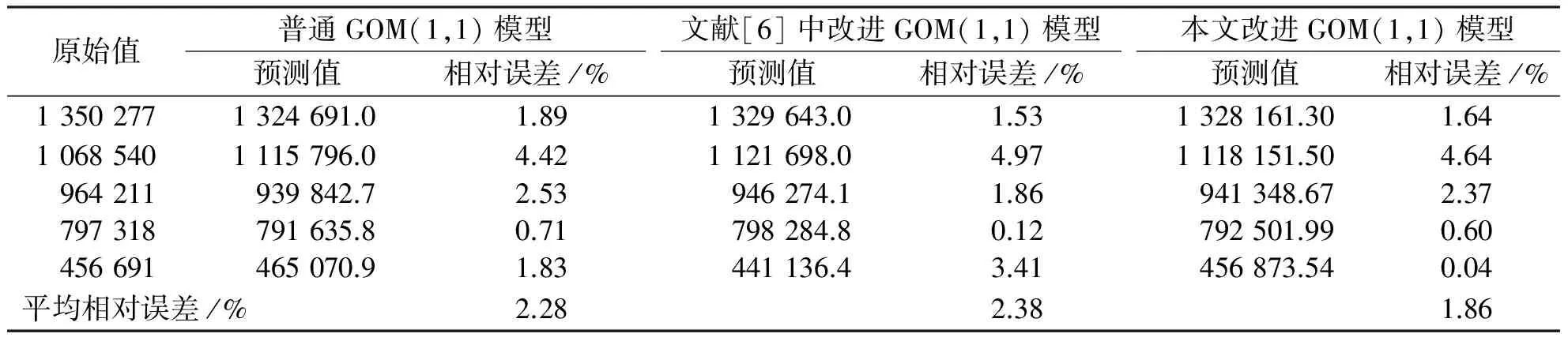
表2 不同模型预测结果

表2的预测结果已经明显证明了本文中的论断，文献[6]中改进的背景值形式并不适合于近似指数序列建模，其预测精度甚至低于普通的GOM(1,1)模型，而本文改进背景值形式显然更适合于近似指数

表3 原始数据

序列建模，其将普通GOM(1,1)模型的模拟平均相对误差由2.28%减小到了1.86%，提高了预测精度.

例2对于指数序列x(0)(k+1)=10 000e-2k,k=0,1,2,3,4.原始序列值见表3.

以上述序列建立文献[6]中改进GOM(1,1)模型，并求出相应的时间相应式：

建立本文改进GOM(1,1)模型，此时背景值权值为定值，根据

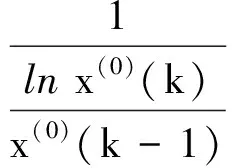
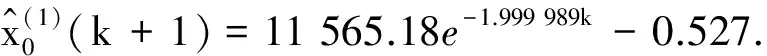
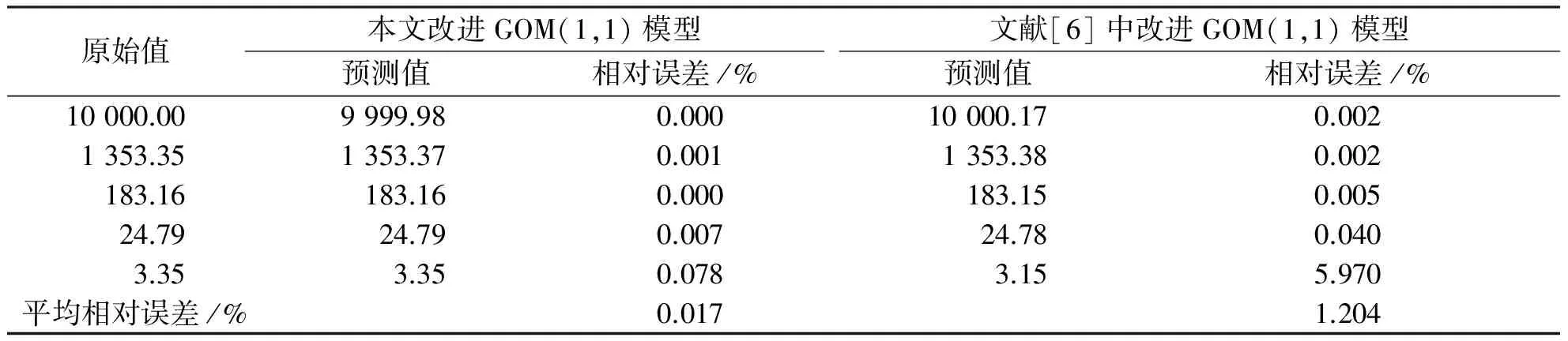
表4 不同模型预测结果

从表4的预测结果可以看出，文献[6]中GOM(1,1)模型的背景值改进形式不仅无法适应于近似指数序列建模，甚至连齐次指数序列也无法完全拟合.对于本文的改进GOM(1,1)模型，其预测误差实际上是由于计算精度的影响造成的，如果忽略精度影响，其理论上是可以完全拟合齐次指数序列的.

4 结 语

文章分析GOM(1,1)模型背景值构造改进形式的建模适应性问题，利用一种已存的背景值构造形式，建立了齐次指数序列下的定权背景值构造形式和近似齐次指数序列下的变权背景值构造形式，实例应用结果显示新背景值形式下的GOM(1,1)模型不仅可以完全拟合齐次指数序列，也适合于近似齐次指数序列建模，提高了GOM(1,1)模型的应用价值.

[1] 邓聚龙.灰预测与决策(修订版)[M].武汉：华中科技大学出版社，2002:1-5.

[2] 刘思峰，党耀国，方志耕.灰色系统理论及其应用[M].北京：科学出版社，2004:1-3.

[3] 陈鹏宇.单桩极限承载力非等步长灰色GM(1,1)模型预测精度分析[J].工程建设与设计，2009(9)：68-71.

[4] 谢开贵，何斌，谭界忠,等.一种灰色预测模型的新方法[J].系统工程理论与实践，1998，18(7)：69-75.

[5] 宋中民，邓聚龙.反向累加生成及灰色GOM(1,1)模型[J].系统工程，2001，19(1)：66-69.

[6] 杨知，任鹏，党耀国.反向累加生成与灰色GOM(1,1)模型的优化[J].系统工程理论与实践，2009，29(8)：161-164.

[7] 王正新，党耀国，刘思峰.基于离散指数函数优化的GM(1,1)模型[J].系统工程理论与实践，2008,28(2)：61-67.

[8] 谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践，2000,28(4):98-103.