考虑电磁机械耦合效应的电磁超声数值模拟方法
武文晶,裴翠祥,陈振茂
(西安交通大学教育部强度与振动重点实验室,西安 710049)
电磁超声无损检测技术近年来在工业中得到越来越广泛的应用。对电磁超声信号的数值模拟是优化和改进检测装置、量化结果及综合分析的重要途径。一般的数值模拟往往忽略速度效应引发的附加涡流,为了全面分析这种电磁机械耦合效应对模拟结果的影响,笔者开发了针对考虑电磁机械耦合效应的模拟程序,验证了其有效性,并对多种条件下的模拟结果分析耦合效应的影响。
1 数值模拟方法
如图1,当激励线圈中通有交变电流时,导体表面会感应出同频率涡流,在磁场的作用下,引发交变洛伦兹力,从而使质点振动产生超声波[1]。
采用静态磁场条件,利用退化向量位法(Ar)来模拟感应涡流,通过波动方程求解质点振动的位移和速度,同时对洛伦兹力和感应涡流考虑电磁机械耦合效应。以下将对各部分方法详细说明。
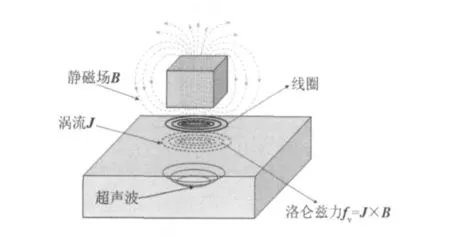
图1 电磁超声机理
1.1 考虑耦合效应的Ar 方法及控制方程
对于低频涡流场问题,其控制方程为:在空气中

在导体中
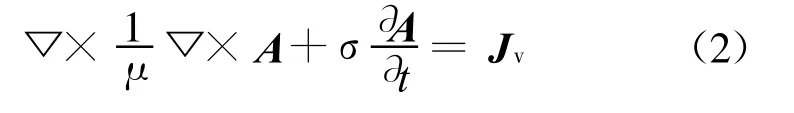
式中Jv=σ[v×(Bm+▽×A)] ,为耦合项。
若定义:
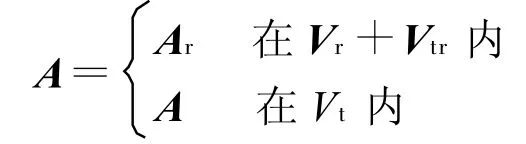
则式(1)和(2)可归并为如下全域有效的方程:
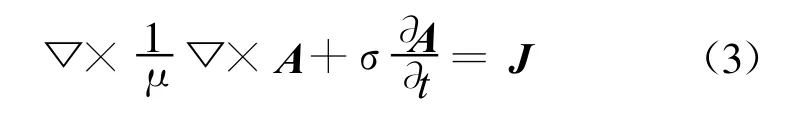
对上式采用棱边元离散化后, 可由C rank-Nicholson 直接积分法求解[2]。
1.2 超声波传播的模拟
根据弹性力学,超声波在介质中传播满足波动方程:
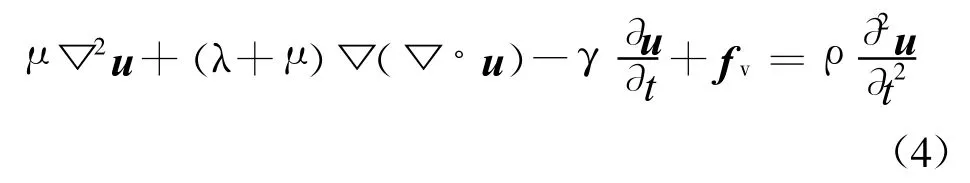
式中λ,μ为材料弹性常数;γ为材料的阻尼系数;ρ为材料密度;u为质点位移矢量。
在电磁超声模型中,如记t时刻介质中的涡流大小为{Je}t,涡流场位函数为{A}t,则有{Je}t=-σ这时,洛仑兹力体载荷为:
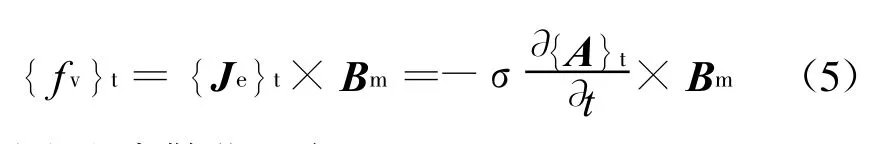
对波动方程离散化后有:

采用显式积分改进算法[3]即可求解位移和速度。
1.3 耦合问题的特殊处理
1.3.1Jv的简化
根据电磁感应原理有:
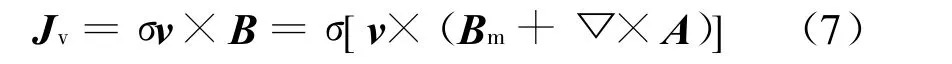
式中Bm为静磁场的磁通密度;▽×A为涡流引起的附加磁场的磁通密度。由于涡流的集肤效应,▽×A常常不到Bm的1%,故可以忽略,进而Jv可简化为:

1.3.2 节点编号对应
本方法建立了涡流模拟和超声波模拟两种模型,由于两者分别采用12 条棱边元和8 个节点的六面体单元,且超声波模型仅包含导体部分,而涡流模型包括了导体和空气两部分,故在耦合项的处理中必须找到两个模型相对应节点的编号。
为解决这一问题,本程序在两种网格划分中采用同样大小的单元且节点编号顺序一致。由于涡流模型中导体区域内的节点即也存在于超声波模型中,可找到超声波模型中其对应位置的节点编号存贮在一维数组中。针对涡流模型中的空气部分节点,则直接设置数组对应值为0。调用该数组即可方便地在两种网格之间转换其他变量。
1.3.3 速度转化
由于采取了不同单元,速度在两种模型中表达式不一样,需要进行转换。
2 数值模拟程序设计、验证及算例
2.1 程序设计及计算模型
基于电磁机械耦合,本程序采用分步代数积分的办法,即上一步所求得速度用于计算下一步涡流大小,该涡流又用于计算下一步速度值。
图2 所示计算模型采用单匝方形线圈并施加垂直方向的磁场。试件为非磁性不锈钢材料,其导电率σ=0.11×107 S/m,泊松比ν=0.33,弹性模量E=1.97×1 011 N/m2,密度ρ=8.03×103 kg/m3。模型为60 mm ×60 mm×30 mm 的平板,脉冲激励信号频率f=500 kHz,电流密度幅值Js=1.25×107 A/m2。

图2 计算模型
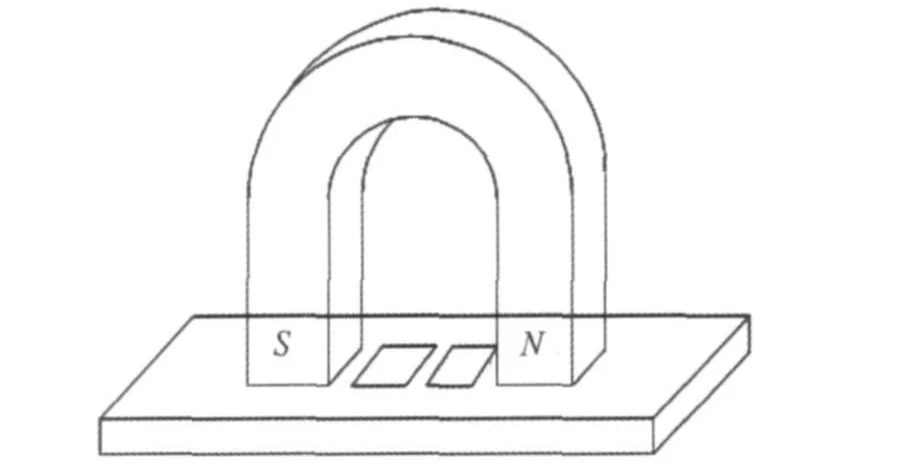
图3 吕字型线圈模型
2.2 程序正确性验证
接收模型表面中心点随时间的的位移变化信号,即可得到电磁超声的检测信号波形。从发射超声波到接收到反射信号,超声波所传播的距离为两倍模型厚度。根据两次反射波信号时间差,可分别算出纵波和横波的波速。表1 为波速的计算结果与该材料理论波速的比较。表1 说明计算结果精度基本可达到要求。另外,由纵波与横波在整个导体中的传播和反射的声场图也可确认数值模拟的正确性。
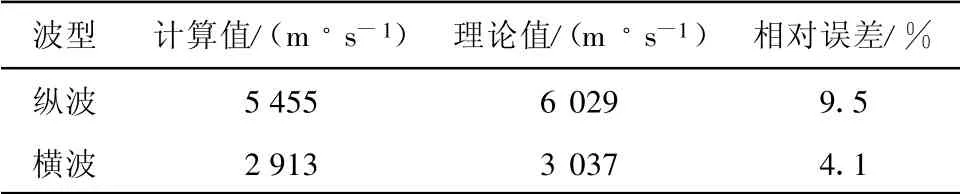
表1 波速对比
2.3 算例分析
2.3.1 耦合效应对波动的影响
为考虑耦合效应对波动的影响,对6 mm×4 mm吕字型线圈(图3),采用300,500,1 000 kHz 激励电流频率的检测信号变化进行了计算,图4 为考虑和忽略耦合效果的计算结果。根据这些模拟结果可知,导体质点的振幅随着频率的提高而增大。耦合效应对振动幅值有影响但几乎不影响振动状态,且影响程度随时间衰减。在计算中也发现,考虑耦合效应的计算时间明显延长,几乎为忽略耦合效应时的两倍。

2.3.2 耦合效应对洛伦兹力的影响
图5 为蛇形线圈模型,图6 为蛇形激励线圈时的波动信号和洛伦兹力的时间变化。结果明显看出,耦合效应的影响在激励消失时刻最为显著并随时间而衰减,洛伦兹力也由此时开始衰减。当考虑耦合时,一旦激励消失,洛伦兹力直接突跳为零;而考虑耦合效应时,洛伦兹力却是逐渐衰减的。这是由于振动速度的变化是个逐渐衰减的过程,考虑耦合时即使激励电流消失不再产生涡流,速度引发的附加涡流仍继续感应洛伦兹力,直至速度衰减为零。
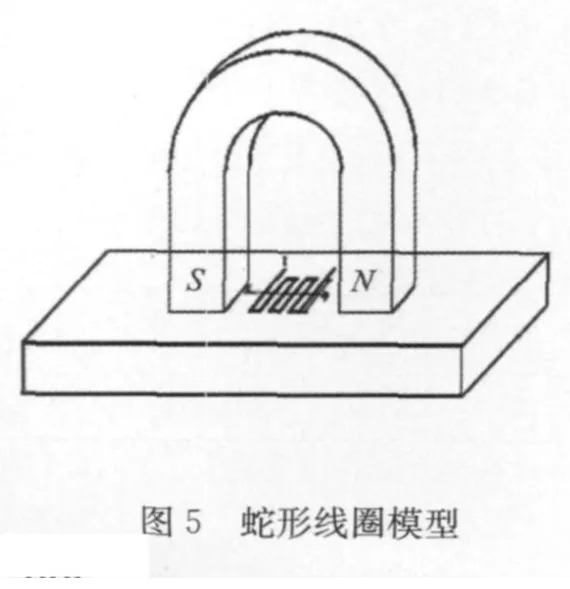
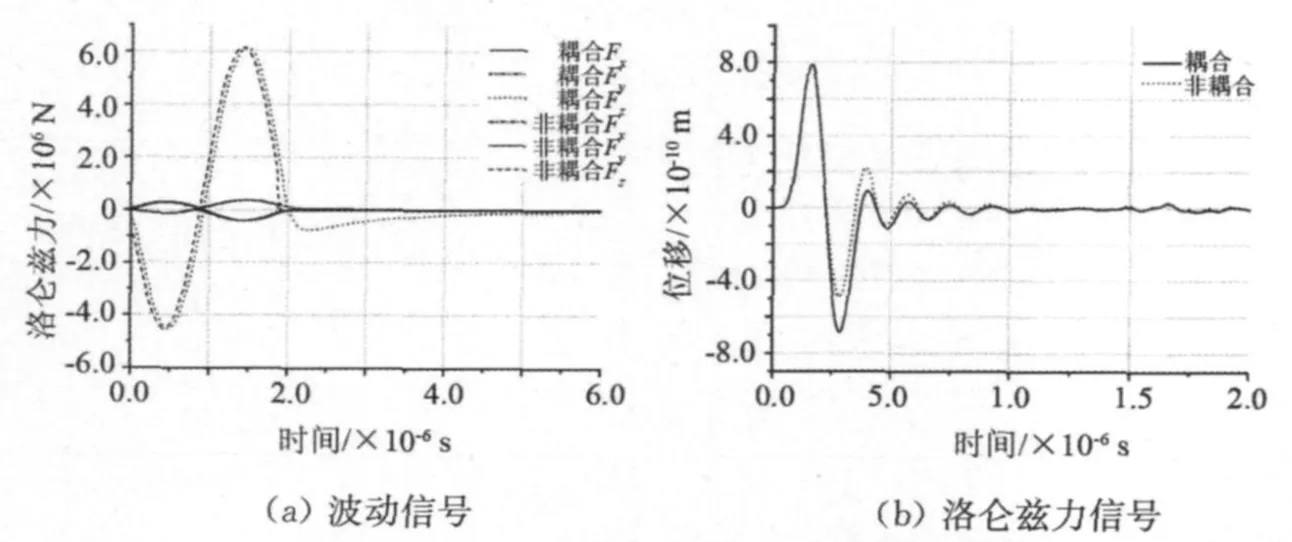
图6 蛇形线圈及其数值模拟结果
3 结论
建立了考虑耦合效应的电磁超声数值模拟方法,对相应的耦合项进行特殊处理,并基于此编写了数值模拟程序。此程序可以应用于多种模拟条件,包括多层结构模型。分析模拟结果得到以下结论:
(1)在激励消失的时刻,耦合效应对于波动幅值有较大影响,该影响随时间逐渐减弱。
(2)耦合效应对洛伦兹力的影响表现为使得洛伦兹力逐渐衰减为零。
(3)当对结果的精度要求并不高时,可以忽略耦合效应的影响。
[1] 朱红秀, 吴淼, 刘卓然.电磁超声传感器机理的理论研究[J] .无损检测,2005,27(5):231-234.
[2] 松本善博.材料缺陷定量评价研究[D] .大阪:大阪大学, 2000:17-78.
[3] Cuixiang PEI, Zhenmao CHEN.Development of Simulation Method for EM AT Signals and Applications to TBC Inspection[D] .Xian:Xi'an Jiaotong University,2009.
[4] Zhenmao Chen, Hideyoshi Takashima, Kenzo Miya.A hybrid database approach for simulating signals of remote field eddy current testing[J] .International Journal of Applied Electromagnetics and Mechanics,2003(18):1-5.

