蒸汽发生器隔板渗透检查用机器人的精度设计
吴健荣,林 戈,陈怀东,李 明
(中广核检测技术公司,苏州 215004)
机器人工作时,精度目标的实现依赖于一个精度链,精度链中的每一个环节对最终精度有着不同程度的影响,局部的精度过剩除了增加制造成本,并不能提高机器人的功能精度。确定机器人构型后,根据目标精度要求拟定各关节、杆件的精度项目,是机器人结构设计中的一项重要内容[1]。
产生机器人运动误差的根本原因是机器人的D-H名义参数与实际值存在偏差。分析机器人误差的方法主要有:位姿误差建模矩阵法、矢量法、摄动法和基于泛灰数学的误差分析法等[2-8],其实质都是在极限条件下给出机器人运动的最大理论误差。从机器人精度设计的角度而言,这些方法难以给出机器人在整个工作空间内的全局性精度指标。
马培荪[7]和赵永涛[8]等用蒙特卡罗法绘制指定位姿点处机器人的误差概率直方图,再往整个工作空间内推广,得到误差分布曲面图和概率等高线,这对机器人精度设计很有帮助,但是图形的绘制过程比较繁琐。笔者在文献[7-8]的基础上给出概率精度数字指标E10X,及相应的机器人精度设计方法,并对核电站蒸汽发生器PT 检查机器人进行精度设计。
1 机器人的概率精度
1.1 机器人位置误差建模
一般而言,控制机器人的位置误差,会间接地控制机器人的姿态误差。因此,一般只对机器人的位置精度链进行设计。
D-H法用α,a,θ,d对机器人进行运动学建模,机器人末端执行器在基础坐标系的位置分量可用pk(k=x,y,z)表示:

对式(1)两边取全微分得:

因此,机器人末端位置在基础坐标系某一坐标轴方向的误差可近似地表示为:
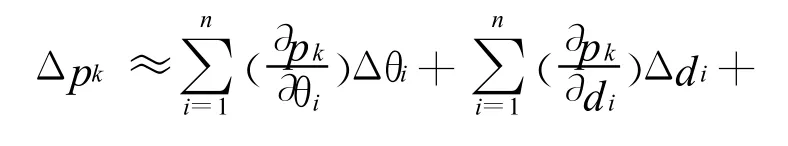

总的末端位置误差可由各坐标轴方向的位置误差合成得到:
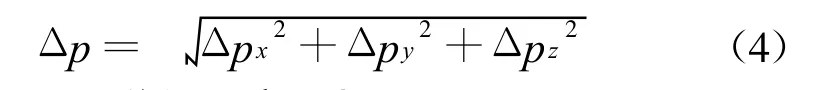
1.2 机器人误差的概率分析
由式(3)和(4)可知,要确定机器人末端误差,必须事先给定机器人的D-H参数及其误差。其中,D-H参数中部分参数取决于末端位姿。因此, 式(3)和(4)不能给出机器人在整个工作空间内的全局精度指标。此外,根据测量原理,D-H参数误差都以一定概率分布规律出现,所有误差源都取极值的概率非常低,将极限误差作为设计指标将产生较大的精度裕量,增加不必要的制造成本。
式(1)给出了机器人末端位置分量的理论值,考虑误差因素后,机器人末端实际位置沿k(k=x,y,z)轴方向的分量可写为:

由式(1)和(5)可给出无需微分计算的误差式:
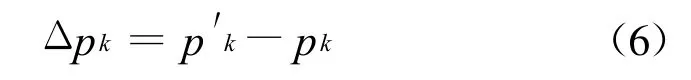
相应地,机器人末端偏离期望位置的距离为:
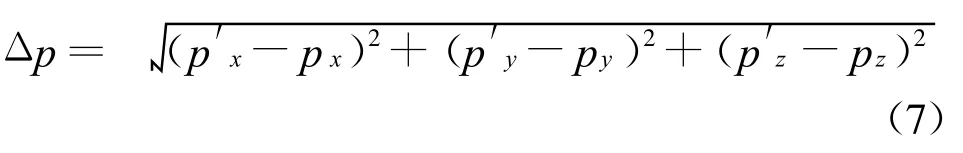
显然,位置误差Δp是D-H参数αi,ai,θi,di及D-H参数误差Δθi,Δdi,Δai,Δαi的函数,可写为:
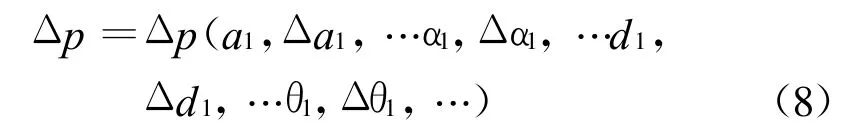
按概率论中心极限定理,当独立的原始误差数目较多时,无论各原始误差具有何种分布,其函数形式的误差值Δpk近似地服从正态分布[7]。
当关节变量q(转动关节qi=θi,移动关节qi=di)给定时, Δpk表示某指定位姿点的位置误差,它近似服从正态分布规律。当关节变量q在许用关节变量范围内随机取值时,Δpk表示工作空间内任意位姿点的位置误差,它也服从正态分布规律(尽管两者的标准差σ值不同), 相应的Δp近似服从Rayleigh分布[7]。
机器人设计时,倾向于在整个工作空间内讨论它的精度指标。满足精度要求的判据是:
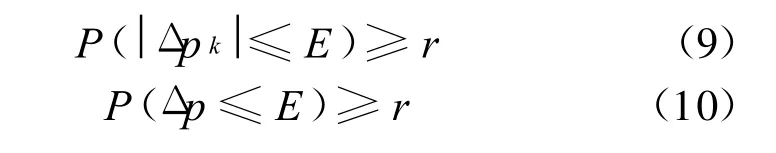
式中E为期望的位置精度;P为样本满足精度要求的统计概率;r为要求的置信概率。
1.3 机器人概率精度指标
用式(9)和(10)进行精度设计时,概率密度函数Δpk和Δp的参数辨识比较困难,为此,可将样本的最大误差作为精度设计指标。定义概率精度指标E10X,字母E的数值对应位置精度,右下标10X表示抽样试验的样本数为10X,如概率精度E107表示抽样样本为107得到的最大误差值为E。
如图1 所示,Δpk近似服从正态分布,误差值正负均有可能。设E-和E+分别为误差样本中的最小值和最大值,误差落在E-和E+之外的概率随|E-|和E+的增大而衰减。理论上,试验样本数越多,E-和E+越趋近于极限误差。Δp近似服从Rayleigh 分布,误差值是非负的,误差落在E+右侧的概率随E+的增大而衰减。理论上,随试验样本数的增大,E+趋近于极限误差。因此,概率精度E10X随样本数的增大而收敛于极限误差,即:
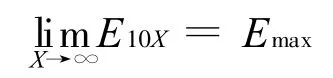
式中Emax为机器人末端位置的极限误差。

图1 机器人位置误差的概率分布
用E10X对机器人进行精度设计时,X值取得越大,E10X越趋近于极限误差值。
2 机器人精度设计的模拟试验方法
计算机软、硬件的发展为大规模的数学试验提供了方便。在M AT LAB 软件平台上,通过模拟试验可方便地得出机器人的概率精度。用概率精度作为设计指标,模拟试验能够直接帮助设计者对机器人精度进行设计。以下给出基于概率精度指标对机器人精度进行设计的基本步骤:
(1)结合机器人正运动学模型,由式(1),(5),(6)和(7)建立机器人D-H参数、D-H参数误差与末端位置精度的计算模型。
(2)根据机器人的D-H参数,建立机器人制造精度等级、运动控制精度与D-H参数误差极限值的对应关系。
(3)由计算机程序模拟产生数量为10X的θi,Δθi,Δdi, Δai,Δαi试验样本,通过模拟试验得到机器人概率精度值E10X,多次循环试验得到不同制造精度等级、运动控制精度与E10X的对应关系。
(4)根据第(3)步结果,拟定机器人制造精度等级和运动控制精度。计算ε=Ep-E10X,若0 <ε<εp,则满足设计要求,结束试验。否则,调整制造精度等级和运动控制精度,直至满足设计要求。其中Ep为期望的精度,εp为允许的精度剩余量。
(5)根据制造工艺条件,具体分配制造公差项目,并根据需要进行个别调整。
值得说明的是,式(1)和(5)都由连杆坐标变换矩阵连续相乘得到, 试验程序的编制很方便。MA TLAB 软件提供了模拟各种分布的随机数,各项误差源的模拟易于实现。此外,用MA T LAB 软件做模拟试验,误差样本允许分批获得,数据样本可以取得很大,从而保证试验结果逼近理论值。
3 蒸汽发生器渗透检查机器人精度设计
3.1 蒸汽发生器PT 检查机器人简介
蒸汽发生器PT 检查机器人是针对EPR 型核电站役前/在役检查研制的,用于蒸汽发生器(简称SG)一回路水室隔板渗透(PT)检查的极限作业机器人。蒸发器水室结构如图2 所示。
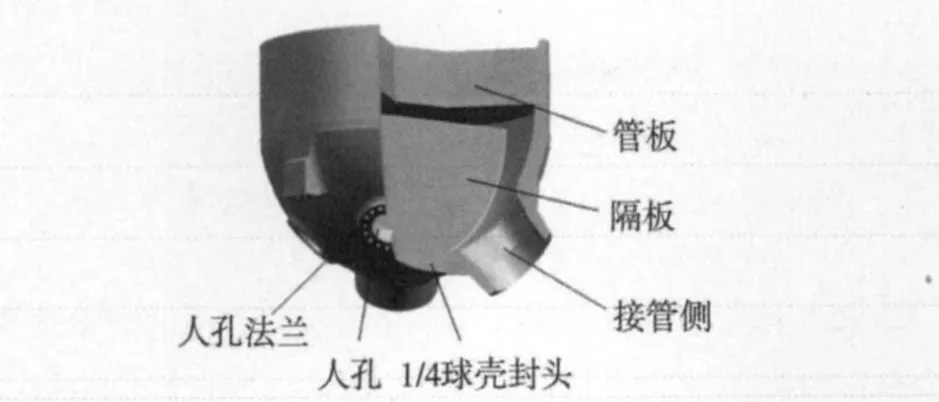
图2 蒸汽发生器水室
蒸汽发生器PT 检查机器人结构如图3 所示,由3 个转动关节组成,D-H参数如表1。

图3 蒸汽发生器PT 检查机器人
3.2 蒸汽发生器PT 检查机器人的精度设计
蒸汽发生器PT 检查机器人的精度设计主要是拟定机器人机械结构的制造精度等级和关节运动控制精度。由于影响机器人精度的客观因素繁多,实际确定D-H参数误差Δθi,Δdi, Δai和Δαi的数值非常困难,这里给出几个基本假设前提:
(1)连杆的长度尺寸公差是导致Δdi和Δai的主要因素,其它各因素导致的Δdi和Δai变化约相当于7 级公差带宽度的20%。
(2)关节旋转运动的同轴度误差是导致Δαi的主要因素,其它因素导致的Δαi变化约相当于该主要因素的50%。
(3)关节运动控制误差是导致Δθi的唯一因素。
根据实际的加工制造条件,设计中可以采用的精度等级为5~11 级。表1 中蒸汽发生器PT 检查机器人的杆长主参数有0 和760 mm 两种。查机械设计手册,可以得到精度等级对应的公差值。结合三个假设条件,求得相应的D-H结构参数Δd i,Δai和Δαi的误差极限值如表2 所示。

表1 机器人D-H 参数

表2 结构参数的误差极限值
为了研究结构参数的角度误差和长度误差对机器人末端位置误差的影响,取样本数量为100 万,分以下三种情况对误差进行概率试验:①令Δαi=0,仅考虑Δdi和Δai。 ②令Δdi=Δai=0, 仅考虑Δαi。③Δαi,Δdi和Δai都考虑。得到位置误差Δp与精度等级的对应关系如图4 所示。
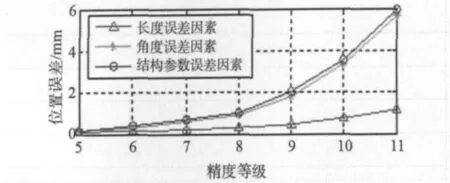
图4 结构参数误差与位置误差关系
由图3 可以看出,公差等级从5~8 级期间,位置误差增加较小,从9 级到14 级,位置误差急剧增大。考虑到装配精度一般要比制造精度低1~2 个等级,为将位置误差控制在1 mm 之内,应该选择7级和7 级以下的制造精度。在制造误差引起的位置误差中,角度参数α的误差因素起主导作用,并且随着公差等级数的增大,引起的位置误差急剧增大,因此在制造过程中应加以严格控制。
考虑实际工厂的加工制造条件和制造成本,整体选择6 级精度制造,个别工艺性较差的尺寸放宽至7 级精度。
按照目前的控制水平,将运动变量误差Δθi在1′~10′间取10 份,在7 级精度的条件下,由模拟试验方法得到末端位置误差与运动变量误差的关系曲线如图5 所示。

图5 运动变量误差与位置误差关系
由图5 可以看出,Δθi对机器人末端位置精度起主导作用。对于蒸汽发生器PT 检查机器人,末端位置误差近似与Δθi成正比关系。为了达到±5 mm的位置精度,总的关节运动控制误差(包括插补计算误差)必须控制在5′以内。由此,拟定关节位置检测精度1′,控制插补计算和伺服误差在5′以内,对机器人结构和控制器进行设计。
由以上基于概率精度指标的机器人精度设计方法,对蒸汽发生器隔板PT 检查机器人精度进行了设计,得到了各个精度环节的设计目标。
[1] 夏水华, 王晓青.PUMA 机器人的精度设计[J] .机械传动, 2001,25(4):16-18.
[2] 焦国太, 冯永和, 王锋.多因素影响下的机器人综合位姿误差分析方法[J] .应用基础与工程科学学报, 2004,12(4):435-442.
[3] Mavroidis C, Dubow sky S, Drouet P, et al.Systematic error analysis of robotic manipulators:application to a high performance medical robot[C] .IEEE International Conference on Robotics and Automation.Albuquerque:New Mexico,1997:980-985.
[4] Freeman J M, Ford D G.Automated error analysis of serial manipulators and servo heads[J] .Journal of Mechanical Engineering Science, 2003, 217(9):1077 -1084.
[5] WU W, Rao S S.Uncertainty analysis and allocation of joint tolerances in robot manipulators based on interval analysis[J] .Reliability Engineering and System Safety,2007, 92(1):54-64.
[6] 罗佑新.泛灰数学在机器人机构误差分析中的应用[J] .机械传动,2003, 27(3):19-22.
[7] 马培荪, 张新辉.工业机器人运动误差的概率分析[J] .上海交通大学学报,1993,27(1):57-63.
[8] 赵永涛, 王田苗, 孙磊.基于蒙特卡洛方法的导航机器人的误差分析[J] .航空制造技术, 2004, 47(3):52-54, 61.

