对一道多根式赛题的探究
2010-12-01 02:11
中学教研(数学) 2010年1期
●
(育才中学 上海 201801)
对一道多根式赛题的探究
●龚新平
(育才中学 上海 201801)
2009年全国高中数学联赛一试的最后一道解答题中出现了含3个根式的和函数最值问题,笔者发现往届全国联赛也出现了类似的问题!本文将首先对该问题给出4种不同的解法,同样的方法也适用于解决含4个或更多根式的最值求解;然后笔者还将在此问题的基础上尝试编拟几道含多根式的最值问题,供读者参考.
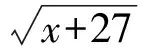
(2009年全国数学联赛试题)
1 4种不同的解法
解法1(调节系数,适度放缩)一方面,由定义域为x∈[0,13]可知
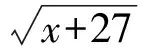
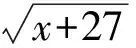


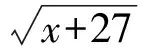
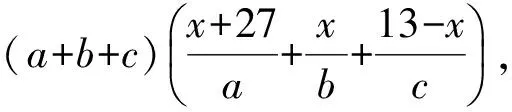

解得x=9.如取k=1,则a=6,b=3,c=2,此时
即当x=9时函数取到最大值ymax=11.
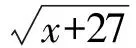
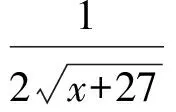
解得x<9,即
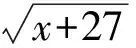
在[0,9]上单调递增,在[9,13]上单调递减,故最大值为f(x)max=f(9)=11,最小值为

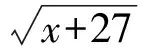
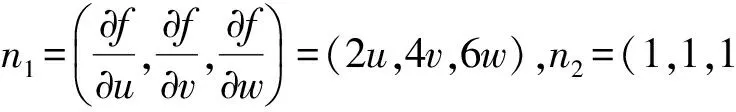
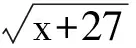
从而当x=9时,最大值为
f(u,v,w)max=f(6,3,2)=11.
在边界处取得最小值,为

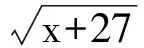
u2+2v2+3w2=66(u,v,w>0).
(1)

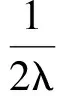
代入式(1)可得
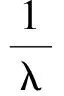
此时,u=6,v=3,w=2,从而最大值为
f(u,v,w)max=f(6,3,2)=11,
在边界处取得最小值,为

2 问题编拟
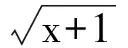
本题是由一道2003年的全国联赛试题改编而来的.
1.7.1 有效性评价指标 ①腹痛发作天数,②腹痛程度,③伴随症状,以上均于基线、治疗后第1、2周记录,治疗结束评价;④中医证候疗效,基线、治疗结束记录,治疗结束评价;⑤腹痛复发情况,治疗结束后4周评价。以腹痛发作天数为主要评价指标。
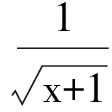
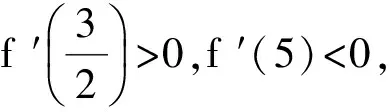
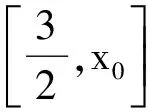
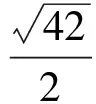
f(x)max=f(x0).
事实上,由Mathematica数学软件解方程(2),易见此时
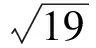
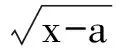
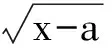
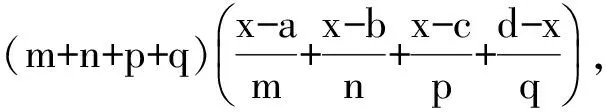
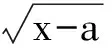
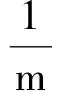
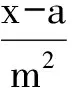
即
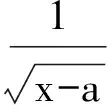
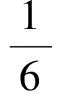
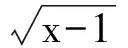
分析由前面的分析不难得出最大值为
f(x)max=f(37)=6+3+2+1=12,
最小值为

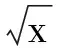
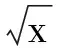
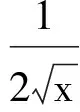
可知,当x>0时,
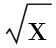
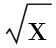
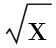
在[0,+∞)上也递增,故
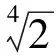
猜你喜欢
中等数学(2022年7期)2022-10-24
中等数学(2022年5期)2022-08-29
中等数学(2022年1期)2022-06-05
中等数学(2022年2期)2022-06-05
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
中学生数理化·八年级数学人教版(2019年2期)2019-12-31
中学生数理化·中考版(2017年3期)2017-11-09

