曲线等误差直线拟合的算法研究及其应用

赵玉刚 于光伟 张 健 刘 肖

(山东理工大学机械工程学院，山东淄博 255049)

目前，多数机床的数控系统只具备直线插补和圆弧插补功能，而实际生产加工中常常会遇到零件轮廓为非圆曲线。此时就需要在给定的精度范围内，用一系列直线或圆弧来逼近它们。直线拟合法因其简单直观而应用较多。直线拟合曲线的方法有：等间距法，等弦长法，等误差法等。等间距法和等弦长法计算较简单但在曲线曲率变化较大的场合不易控制插补精度和节点数。而等误差法能尽可能地减少节点数，适用于曲率变化较大的曲线轮廓［1］。曲线等误差直线拟合节点计算的一般方法是：在已知节点处建立允差圆，联立允差圆与曲线的斜率关系解高次方程组求得切线斜率，后据此斜率建立拟合直线的方程，联立曲线方程求得拟合直线与曲线的交点做为下一个拟合节点。但此算法的弊端有二，一是对高次曲线(如椭圆弧)而言，应用该方法时往往陷入高次方程组的求解中，而确定高次方程组的唯一解往往很复杂；二是该算法没有充分考虑到实际数控加工中，曲线的拐点(如正弦曲线)应该作为拟合节点。据此本文提出了一种基于罗尔定理与二分法的曲线等误差直线拟合新算法，该算法通过将拟合区间适当划分成为多个凹凸性一致的单值区间(若拟合区间已经是凹凸性一致的单值区间则不必划分)，在各个单值区间内运用罗尔定理与二分法迭代求解拟合直线与曲线上对应的弧之间的误差来逐步逼近程序所要求的允许误差。该算法避免了高次方程组的求解，容易控制插补精度，易于实现程序编制和数控加工应用。

1 基于罗尔定理与二分法的曲线等误差直线拟合新算法思想

1.1 曲线等误差直线拟合的一般算法

如图1所示，设零件轮廓曲线的数学方程为y=f(x)。节点坐标计算步骤如下［2］：

(1)以起点 A(xa，ya)为圆心，以允差 δ为半径作圆。其圆方程为

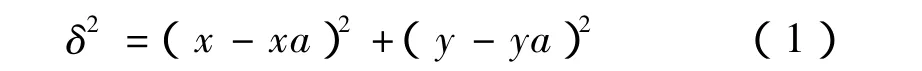
(2)作允差圆与曲线y=f(x)的公切线MN，则可求公切线MN的斜率k

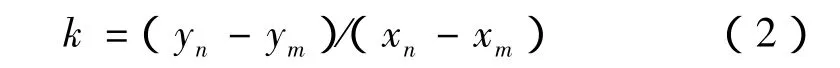
为求 yn、ym、xn、xm，需要解下面的方程组

式中y=F(x)为允差圆方程。

(3)过A点作斜率为k的直线，则得到直线插补段AB，其方程为

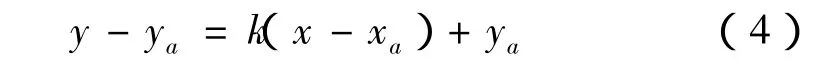
(4)求直线插补节点B点的坐标，解方程组

求得交点B(xb，yb)的坐标值，便是第一个直线插补节点。

(5)按以上步骤顺次求得C，D等各节点坐标。

此算法先求得允差圆与曲线的公切线斜率k，后联立方程组(5)求解得到下一插补点。当要拟合高次曲线时，方程组(3)为四元高次方程组，其求解过程非常复杂且确定唯一解也需要更多的判断条件。另外在实际数控加工中，若曲线有拐点，则拐点应视为拟合节点。

1.2 基于罗尔定理与二分法的曲线等误差直线拟合新算法

如图2所示，设在曲线y=f(x)的一个凹凸性一致的单值闭合区间AB上，用直线段连接曲线的两个端点A、B，则它与曲线形成一个弓形，我们称这条直线为曲线的弦。只要该曲线上的点到弦AB的最大距离hmax小于程序设定的允许误差res，我们就可以用直线段AB来拟合曲线段 AB［3］。而当 hmax大于允许误差res时，就需要运用二分法将区间AB进行划分以找到下一个拟合点F。再连接直线段FB，在曲线段FB上再次进行同样流程操作，最终可得到所有拟合点。

本小节先推导曲线上的点到它对应的弦之间的最大距离公式，后详述二分法迭代求解拟合点的应用过程。

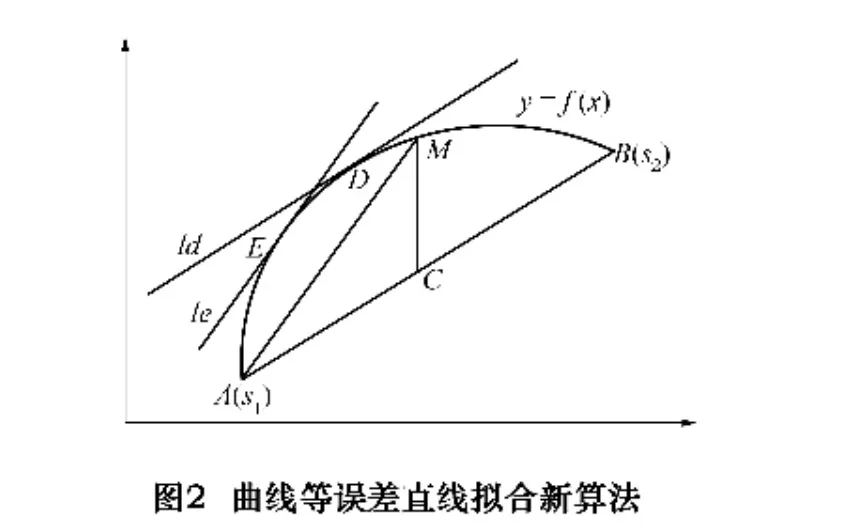
设直线AB的斜率为k，因曲线的AB段为凹凸性一致的单值区间，则由罗尔定理知，在曲线AB上有且仅有一点D，使得曲线AB在该点的斜率kd，有：

而D 点的坐标(xd，yd)可通过方程(7)求得：

弦AB所在直线方程为：

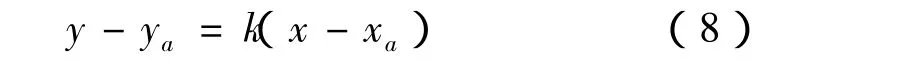
则点 D(xd，yd)到弦 AB 的距离为

由导数的性质及意义可知，曲线AB上的点中，D弦AB的距离最大，且D到弦AB的距离h就是弦AB逼近曲线AB时的拟合误差。

在单值闭合区间AB上，弦AB拟合曲线AB的拟合误差hAB往往大于程序设定的允许误差res，这时就需要在区间AB上运用二分法迭代多次求解弦的拟合误差来逼近允许误差res。二分法应用过程如下：

(1)初始化A点坐标为拟合区间起点坐标(xa，ya)，B点坐标为拟合区间终点坐标(xb，yb)。A点为当前已知拟合点，动点。

(2)将A点赋值给S1点，B点赋值给S2点。S1、S2点为区间二分迭代时用到的点，动点。

(3)计算弦AB拟合曲线AB的拟合误差hAB，赋值h=hAB。

(4)比较拟合误差h与允差res的大小：如果h＞res，转(5)步；如果 h≤res，则区间终点 B作为最终拟合节点，等误差直线拟合过程结束。

(5)取直线段S1S2的中点C横坐标之值xm=(xs1+xs2)/2，计算ym=f(xm)，得到直线段S1S2中点C在椭圆弧上对应的二分点M(xm，ym)。

(6)计算弦AB拟合曲线AM的拟合误差hAM，赋值h=hAM。

(7)比较拟合误差h与允差res的大小：如果h＞res，M 点赋值给 S2；如果 h≤res，M 点赋值给 S1。

(8)计算|fres-h|之值，如果小于或等于指定的误差值，寻找插补点结束，得到新拟合节点F，转(9)；如果大于指定的误差值，返回步骤(5)继续查找。

(9)F赋值给A点，转步骤(2)。

2 凹凸性一致的单值区间的划分

设曲线方程为y=f(x)，拟合区间为x∈［a，b］，允许误差为res。为高质量地拟合曲线，满足数控加工的实际需要，应先判断曲线是否存在拐点，若存在，则拐点应直接作为曲线的拟合点。

若在开区间x∈(a，b)求得y=f(x)的一系列拐点横坐标为 a1＜a2＜… ＜an，则整个闭区间 x∈［a，b］可划分为 n+1 个小区间［a，a1］，［a1，a2］，…［an-1，an］，［an，b］，在这n+1个小区间内可按上一小节的算法求得所有拟合节点。

如正弦曲线y=asin(wx+t)+y0，易知其拐点坐标(xd，yd)满足方程

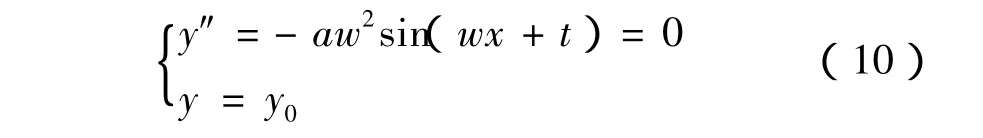
对有些高次隐式非线性方程f(x，y)=0，在其要求的拟合区间内往往为非单值函数，此时也需要通过适当方法将整个拟合区间划分为多个凹凸性一致的单值区间。以椭圆为例，分析此类函数曲线的单值区间划分方法，如图3所示，设椭圆方程为x2/a2+y2/b2=1，拟合方向为逆时针。不妨设当前已知节点为A(xa，ya)，位于第一象限。当下一节点B出现在弧S1S2上时，则AB直线段拟合误差范围是(0，b-ya)，误差上限是在AB平行于X轴时取得的；当下一节点B出现在弧S2S3上时，则AB直线段拟合误差范围是(b-ya，)，误差上限是在 AB关于椭圆圆心对称时取得的，此时直线AB斜率为k=ya/xa。再结合程序设定的允许误差res，可进行如下判别：

表1 椭圆逆圆弧等误差直线拟合区间划分

(2)如果0＜res＜b-ya，则下一拟合点一定出现在弧S1S2上，此区间y相对于x的单值函数，可在此区间二分迭代多次求得拟合点；

(3)如果b-ya≤res＜，则下一拟合点一定出现在弧S2S3上，此区间x相对于y的单值函数，可在此区间二分迭代多次求得拟合点。

若当前已知节点位于其它象限，讨论过程同上。椭圆逆圆弧等误差直线拟合区间划分及拟合误差表达式见表(1)。

3 曲线等误差直线拟合算法流程

基于罗尔定理与二分法的曲线等误差直线拟合算法框图见图4。该算法先判断曲线是否存在拐点，若存在，则应以拐点为边界进行拟合区间的第一次划分；后判断曲线的拟合区间是否是单值区间，若不是，则可通过适当方法进行区间的再一次划分，是整个拟合区间被划分成为多个凹凸性一致的单值区间。在每个单值区间内就可以运用二分法迭代求解拟合误差以逼近允许误差，以此求得拟合点。若函数的整个区间较长且已经是单值区间，则为了加快拟合节点的计算速度，可适当增加附加条件来划分区间以减少迭代次数(如限定拟合直线的长度)。

4 曲线等误差直线拟合的轨迹仿真实例

基于本文算法，以C++Builder 6.0为开发工具，编程实现了几种常见曲线的等误差直线拟合，如椭圆弧、正弦曲线、抛物线、双曲线等。

当椭圆圆心坐标为(100，0)，半轴长 a=300，b=200，起始角度 startangle=30，终止角度 endangle=300，插补方向为逆弧，允差res=8时，其仿真效果如图5，节点计算结果见图6。

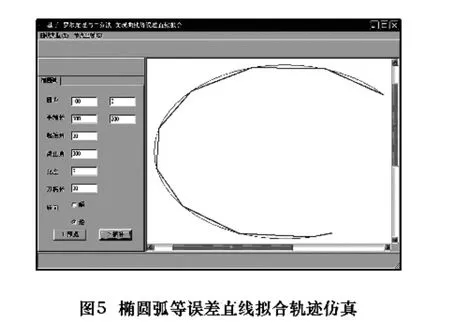
仿真结果表明，由于该算法避免了高次方程组的求解，代之以迭代多次线性求解拟合误差以逼近允许误差，使得节点计算简单可靠，处理速度较快，在线切割，轮廓铣削加工上有较大应用价值。

5 结语

曲线等误差直线拟合的一般解法是设定允差圆的方程后解高次方程组，而确定其唯一解往往很复杂。本文提出了一种基于罗尔定理与二分法的拟合方法，其思想是先将整个拟合区间适当划分成为多个凹凸性一致的单值区间，后在这多个单值区间内二分迭代多次求解弦与对应的曲线弧之间的拟合误差来逼近允许误差，体现了正难则反的逆向思维。该算法避免了高次方程组的求解，容易控制拟合精度，易于实现程序编制，在数控加工中有较大应用价值。

［1］于洋，魏娟.等误差直线逼近非圆曲线节点计算新方法［J］.组合机床与自动化加工技术，2005(5)：32-33.

［2］赵玉刚，宋现春主编.数控技术［M］.北京：机械工业出版社，2003.

［3］周晓铭，陶俊才，等.基于二分法的曲线等误差圆弧拟合算法及其应用［J］.南昌大学学报，2008(1)：100-102.

［4］王丽萍，孙国防，等.非圆曲线数控编程的等误差逼近及其实现［J］.现代制造工程，2006(10)：30-32.