三坐标测量机测头半径补偿技术及应用

王红敏

(山东理工大学机械工程学院，山东淄博 255049)

各种曲线与曲面形状复杂，有时还有较高的精度要求，因此很难测量。在精密测试领域，计算机辅助测试技术(Computer Aid Test简称CAT)使得复杂工件的测量简单化，不仅能完成尺寸、曲线、曲面的精密测量，还能进行形位误差的精确评定。其最典型的代表是三坐标测量机(Coordinate Measuring Machines简称CMM)，它的出现标志着计量仪器从传统的手动测量向现代化的自动测试技术过渡的一个里程碑。三坐标测量机通用性强，测量范围大，性能好，效率和测量精度高，当测球与被测工件接触并沿着被测工件的几何型面移动时，就可获得被测几何型面上各测点的几何坐标，并由计算机计算出被测的几何尺寸和相互位置关系，完成各种复杂零件的测量，符合机械制造业中柔性自动化发展的需要。因此，它已发展成为一种大型精密测量仪器，成为与加工中心对应的测量中心［1］。本文着重进行三坐标测量机测头半径补偿技术研究。

1 二维补偿技术

三坐标测量机接触式测头测量曲线、曲面时，坐标测量机给出的是测头球心的轨迹。由于测球总是有一定的半径r，当被测点的表面法矢方向和测轴方向一致时，测点坐标和测头中心相差一个测头半径r值，因此它是与被测曲线、曲面相距r的包络面。所以应对测量数据进行测头补偿，即在用三坐标测量机测得代表球心轨迹的曲线、曲面后，需要进行测头半径补偿，求出与球心轨迹相距r的包络线、包络面，从而构建出所要求的曲线、曲面［1-4］。

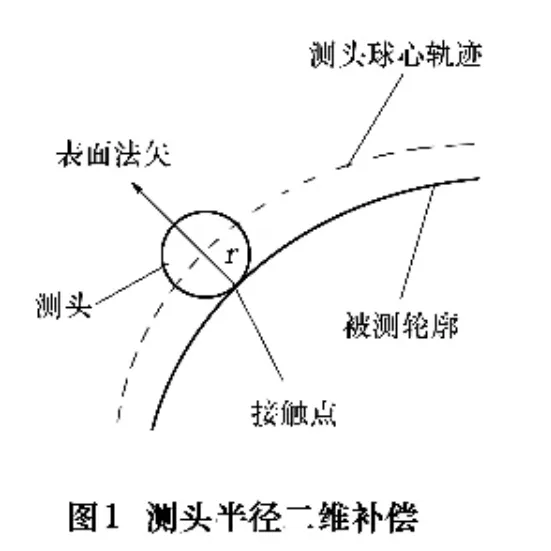
如图1所示，测量点连线为平面曲线。当测头的压力矢和测量截面不在一个平面时，测量点连线为空间曲线。

如果被测曲面的形状已知，并可以用一定的解析函数表示，那么就可以用解析的方法求出曲面各点的法线方向，按照求得的法线方向确定测得的球心轨迹上与之相对应的点，对它进行测头半径补偿。

(1)常用二维补偿

目前的CMM测量中，广泛采用一种二维自动补偿方法。即在测量时，将测量点和测头半径的关系都处理成二维情况，并将补偿计算编入测量程序中，在测量时自动完成数据的测头补偿，如图2a的斜面测量。这种补偿方法简化了补偿计算，不影响测量采点和扫描速度，对一些规则形状的表面测量更为简便、精确。

因为测头接触工件时，三坐标测量机接收到的坐标值是红宝石球头中心点的坐标。显然，测量软件将自动从接触点沿着测量逼近方向回退一个测头半径值。但补偿后的点并非真正的接触点P1，如图2b所示，而是测头沿着测量逼近方向上的点P2。这样就会在正确的逼近方向上产生补偿误差δ。产生误差的大小与测头的直径及该工件与直角坐标系中坐标轴的夹角有关，夹角越大，误差越大［5］。

图2b中r为测球半径，α为测量逼近方向和正确逼近方向之间的夹角，δ为补偿误差。由图2可知

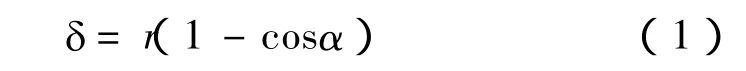
由式(1)可以看出，测球半径r越小，补偿误差δ也越小，因此当进行点位测量时，应选用尽可能小的测球。当角度α为0时，其补偿误差δ也为0；角度α越大，其补偿误差δ也越大，所以，测量时要尽可能使测量逼近方向与被测表面法矢相一致，以使测头沿着被测表面的法线方向移动。下表为测球半径r=1 mm时的二维补偿误差。

表1 测头半径二维补偿误差

目前CMM的测量程序中都具有进行实时补偿功能，即在数据测量过程中，每次采点后，测量程序自动计算其补偿量，最终记录输出补偿过的数据点集，但多采取上述的二维补偿方法。显然，由上述误差分析可知：经过补偿的工件尺寸比实际工件实体尺寸略大。如果所测表面为规则形状，α为定值，则可以通过修正δ来加以消除；但当被测表面为自由曲面，表面是挠曲的，则随测点位置不同ã角也在改变，就必须采用三维的测头半径补偿。

(2)三点共圆法补偿

在精度要求不高、曲线比较简单时，先测量被测表面，得到测头中心的数据，可用作图的方法，求得包络线来得到实际曲线［2］。但为了提高精度，需要数学方法求得测头中心坐标的法线方向，依此求得实际轮廓，具体过程如下：

假设在曲线、曲面上测得n个点，先取曲线上三个连续的测量点P1(x1，y1)，P2(x2，y2)，P3(x3，y3)，如图3所示。

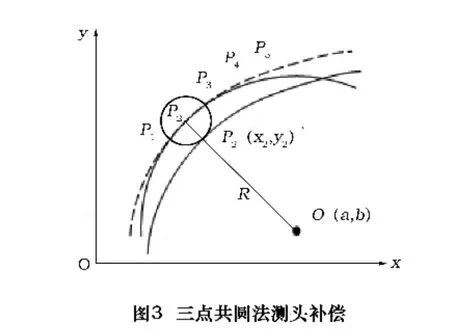
当三点连续曲线段很小时，可看作是一段圆弧上的点，P1、P2、P3三点均满足圆方程，求解该方程，得到P1、P2、P3所在圆弧的圆心坐标 O(a，b)及圆半径 R。连接P2和O，P2O即为过P2点的圆弧法线，以P2为圆心，半径为测头半径r的圆与P2O交点P'2(x2，y2)，即为实际曲线上的点。再根据三个连续测点，求出P'3，以此类推，求出 P'4、P'5、…、P'n-1。三点共圆法仅适于二维状态下的测头半径补偿，如平面凸轮测量时可采用该方法。测头半径的二维补偿实例如图4。

2 三维补偿技术

由以上分析可知，对一些规则形状表面(如平面、二次曲面等)的测量，二维补偿是精确的。但对于一些由自由曲面组成的复杂曲面，测量时测点位置的曲面法矢通常和测轴方向不同，此时按二维补偿计算会存在误差。在误差不能忽略的情况下，必须考虑对测量数据进行测头半径的三维补偿［6-7］。要实现测头半径补偿，必须知道被测轮廓或者测量探头与曲面接触点的法矢。因此，进行测头半径补偿的核心问题就是确定被测轮廓各点的法矢。

我们知道，自由曲面一般无法用解析函数表示，因此也难以用解析方法求其包络面。如果在测得大量测球中心轨迹数据后，能用建模的方法得到一个近似的解析表达式逼近它、代替它，也就可以根据这一解析式求出测球中心轨迹面各点的法线方向，从而进行测球半径补偿。根据建模理论，可以用曲面拟合法实现自由曲面测量时测头的三维补偿。为了求测球球心轨迹的包络面，必须知道曲面的法线方向，由测得的球心O沿着曲面的法线方向向曲面移过距离r，即可以得到测头与被测曲面的接触点P。很显然，测头半径补偿需沿三维曲面的法向进行，如图5所示。

能够实现三维补偿确定曲面法向经常用的是微平面法、微球面法、曲面拟合法等［8-10］，简单介绍如下：

(1)微平面法 为了确定被测曲面的法向，如图6所示，可以在P点附近测若干个点，例如测P1、P2、P3三个点(也可以取多点)，然后通过 P1，P2，P3三点作一个平面，这一微小平面的法线即可视为曲面的法线。

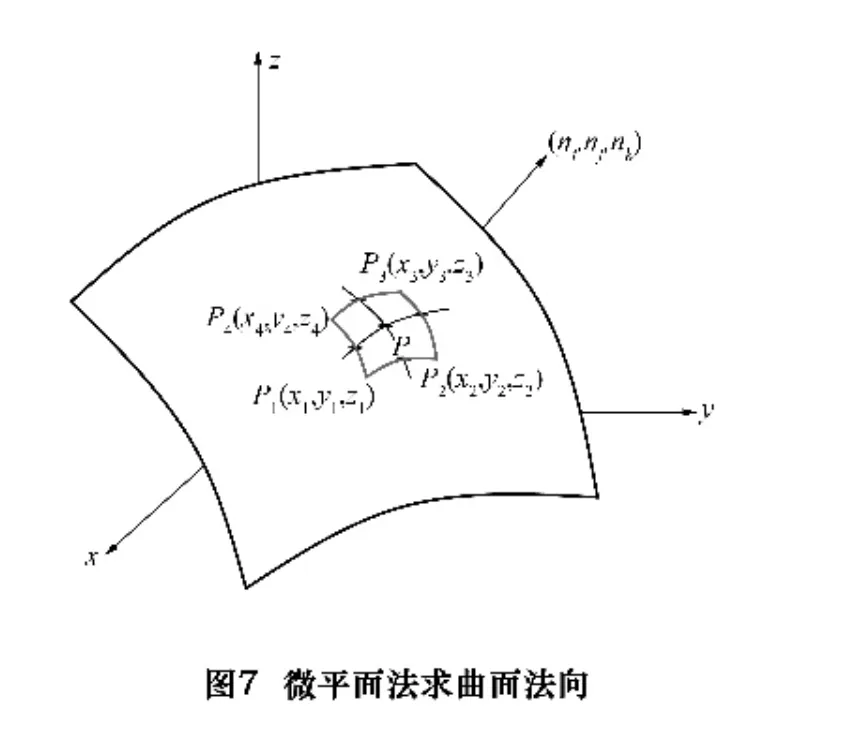
实际测量中，往往采用网格法(三角网格法或多点网格法)，如图7所示。为了确定P点的法线方向，这里采用方形网格，但不是简单地在P点附近再去测4个点，而是利用与它相邻近的4个网格点P1、P2、P3、P4，然后用最小二乘法确定它的最佳拟合平面及其法线方向。值得注意的是，在实际测量中，直接得到的并不是测量点P与 P1、P2、P3、P4的坐标，而是测量 P 点和Pi点时测端球心位置O及Oi的坐标，必须根据这些拟合平面的法向进行测头半径补偿，才能得到P和Pi诸点坐标值。在测点的布置上，P1～P4等点的距离要适中，不能相距太远，也不能相距太近。相距太远，求得的平面就会偏离被测曲面的切面，不能得到准确的补偿半径；也不能相距太近，因为每一点的测量都伴随有测量误差，在相同的测量误差情况下，点与点的距离越小，求出法线方向误差越大，因此相邻点的位置，需根据被测曲面的曲率半径、测量误差的大小选择。

(2)微球面法 微球面法同微平面法相似，是对点P及其相邻的4个网格节点P1、P2、P3、P4用最小二乘法拟合一个最佳微球面，同样这个微球面为测端球心点位置Oi形成的球面，需要进行测头半径补偿才能得到被测点的坐标。设该微球面中心为C、半径为R，则在CO连线上，与C相距R±r的点(其中r为测球半径)，才是经测端半径补偿后求得的被测曲面上的点。用微球面法进行半径补偿，同样存在各个Pi点不能相距太近或太远，测量不确定度的大小直接影响求得的法线方向。

(3)曲面拟合法 对没有数学函数表达式的曲面，不能用解析的方法求取自由曲面各点的法线方向。如果在测得大量测球中心轨迹数据后，用建模的方法将一个近似的解析表达式逼近它、代替它，也就可以根据这一解析式求出测球中心轨迹面各点的法线方向，从而进行测球半径补偿。

曲面拟合法属于测量完成后事后数据处理，即根据测头半径、表面曲面的性质和所采取的测量方法来计算每个点的补偿量或采取其他方法处理补偿问题。同微球面法一样，计算较为烦琐，工作量也大，适合处理复杂曲面和轮廓曲线的补偿问题。核心是根据测量点云信息计算接触点的法矢。

本实验研究中采用微平面法补偿，计算简单，精度可靠。测量时测头在应测点P的一个小邻域内，分别采集三个参考点P1(x1，y1，z1)、P2(x2，y2，z2)、P3(x3，y3，z3)，如图6 所示。由于 P1、P2、P3距被测点 P 较近，故可以用该三点组成的微小平面的法矢近似作为P点的法矢(nx，ny，nz)，进行半径补偿。其计算方法为

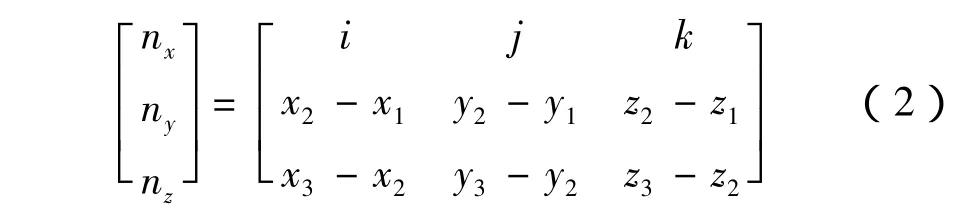
对上述数值进行单位化处理，即可得到被测点的单位法向矢量，表面被测点的坐标 P(xP，yP，zP)为

其中O(xO，yO，zO)为球心点的坐标。这种方法适用于复杂曲面的手动和自动测量。在多点测量的情况下，可进行多点网格化处理。本文所采取的方法即是微平面法的多点网格化处理方法，该补偿方法针对测点较多的情况，简单实用，可用计算机进行数据处理，从而计算出被测点的坐标值，测量实例如图8所示。

以意大利Coord3公司的ARES10-7-5桥式测量机为测量工具，凸轮轮廓经三坐标测量机测量后，以文本文件格式输出，直接读取测量结果，可以根据需要设定直角坐标或极坐标输出。图9所示为得到的红宝石测球中心点的坐标及测头经过补偿后的被测轮廓点的坐标，以直角坐标的形式显示，补偿后的点形成的轮廓线即为凸轮的实际廓线。

将上述数据读入 UG、PRO/E、ImageWare(Surfacer)等各种逆向工程软件，即可快速得到凸轮的实际表面廓线。然后根据软件的功能，可以根据需要与理论廓线进行比较，或做出所需的零件三维实体模型，快速直观地了解产品的形状，为设计制造提供可靠的理论依据。如图10所示，是在ImageWare软件中的凸轮轮廓线，外侧的曲线为测量形成的测头球心轨迹线，内侧的曲线为测头直径φ4.001 mm经过补偿以后的凸轮实际轮廓线。如果凸轮为内凹型，则应向外侧补偿测头半径，以得到实际的凸轮轮廓线。

3 结论

本文通过对三坐标测量机测头半径的二维和三维补偿技术的分析及应用研究，进一步阐明了测头补偿技术的核心问题与关键技术，具有较强的适用性，将对曲线、曲面的测量具有重要的意义。

(1)对一些规则形状表面(如平面、二次曲面等)的测量，二维补偿是精确的。但对于一些由自由曲面组成的复杂曲面，测量时测点位置的曲面法矢通常和测轴方向不同，此时按二维补偿计算会存在误差，在误差不能忽略的情况下，必须考虑对测量数据进行测头半径的三维补偿；

(2)要实现测头半径补偿，必须知道被测轮廓或者测量探头与曲面接触点的法矢，因此，进行测头半径补偿的核心问题就是确定被测轮廓各点的法矢；

(3)能够实现三维补偿的是微平面法、微球面法、曲面拟合法、三角网格法等。由于曲面拟合法和三角网格法属于测量完成后事后数据处理，且同微球面法一样，计算较为烦琐，工作量大，故适合处理复杂曲面和轮廓曲线的补偿问题。其核心是根据测量点集信息计算接触点的法矢。微平面法适用于复杂曲面的手动和自动测量，计算简单，精度可靠，微平面法的多点网格化处理方法，对测点较多的情况，方法简单实用，且可计算机进行数据处理，从而可方便快速计算出相应被测点的坐标值。

［1］张国雄著.三坐标测量机.天津：天津大学出版社，1999.

［2］金涛，童水光著.逆向工程技术.北京：机械工业出版社，2003.

［3］来新民，黄田，曾子平，等.自由曲面逆向工程系统的研究.中国机械工程，2000，11(7).

［4］K.Skalski，et al.Identification and Geometrical Modeling of/complex Shape/surfaces using/coordinate Measuring Machine and CAD/CAM System.Journal of Materials Processing，1998(76)：1-3.

［5］王红敏，石沛林.坐标测量机的测头及测针半径误差补偿［J］.工具技术，2003(7).

［6］冯国馨，张国雄，解则晓.CMM曲线曲面测量领域的关键问题，航空精密制造技术，1999，35(6).

［7］侯宇，崔晨阳，张竞，等.三坐标测量机上自由型曲面的精确测量.宇航计测技术，1999(12).

［8］尹明富.空间凸轮机构设计、误差分析与单侧面加工理论及实验研究：［博士学位论文］.西安：西安理工大学，2003.

［9］C.Menq，F.L.Chen.Curve and Surface Approximation form CMM Measurement Data.Computer and Industry Engineering，1996，30(2).

［10］王国兴.用三坐标测量机对空间曲面的测量.计量技术，1995(11).