分形建筑审美*

冒亚龙, 何镜堂

(1. 长沙理工大学 建筑系， 湖南 长沙 410004； 2. 华南理工大学 亚热带建筑科学国家重点实验室， 广东 广州 510640)

分形建筑研究最早可以追溯到分形创始人曼德布罗特(B.B.Mandelbrot)， 他率先提出“在建筑学的历史上， 密斯·凡·德·罗的建筑是限定比例的， 是对欧几里德的回归， 而装饰艺术的建筑则体现了丰富的分形特征。”[1]1-3随后， 巴迪(M. Batty)、 隆雷(P. Longley)、 卡尔·巴维尔(Carl Bovill)运用分形计盒维数的方法计算建筑分维值， 并以此量化研究建筑。[2-3]李得仁和廖凯对中国古代建筑和城市空间形态模式与分形图形进行了比较， 阐述了规则与非规则的城市和建筑分属不同的分形类型。[4]李世芬等也对建筑维度进行了比较研究。[5]这些研究从宏观视角考察建筑， 采用分形量化分析和比较的方法， 对建筑图形进行分形计算， 据此对古代建筑与现代建筑进行了审美比较分析。美国数学家塞灵格勒斯(Nikos A.Salingaros)致力于从分形科学的角度探求建筑的基本法则， 进而发展出一套关于建筑形式的数学理论。[6]他建立起关于建筑尺度层级的定律， 提出相邻尺度之间的比例为e=2.718， 指出丰富而连续的尺度层级是传统建筑较现代主义建筑更具活力的内在原因。[7]卡尔·巴维尔认为分形是建筑学一种强有力的工具， 既可评价建筑， 又可利用分形生成复杂的韵律， 使建筑与周围环境取得协调。[3]洛仑兹(Wolfgang E. Lorenz)延续了卡尔·巴维尔的分形建筑研究。[8]赵远鹏、 于雅琴的硕士论文探讨了分形理论以及在建筑领域的初步应用。[9-10]本人与雷春浓也对分形美学及其建筑设计评价做了一些探索。[11]克朗普顿(A· Crompton)和撒拉(N· Sala)从分形理论角度阐释了建筑与环境的有机联系。[12-13]

分形理论在建筑设计与评价领域显示出了独有的艺术魅力， 成为设计艺术界越来越重要和广泛的讨论话题， 但多数囿于分形几何和计算机模拟分形层面， 停留于分形建筑欣赏和评价， 而缺乏对分形建筑创作原理或美学思想的深入分析和探索。对分形建筑美学的理论与方法研究旨在弥补这种不足， 并为分形建筑理论研究奠定基础。

一、 分形理论

分形作为一门以非规则几何形状为研究对象的学科， 由法国数学家曼德布罗特1975年建立。作为一门新兴学科， 分形理论与耗散结构和混沌理论被誉为二十世纪科学的三大发现。它认为在一定的条件下， 事物的局部在某个方面(形态、 结构、 信息、 功能、 时间和能量等)表现出与整体的相似性， 并认为在极度复杂的现象背后存在着意想不到的简单规则。分形理论主要由作为分形的定量表征和基本参数的维数理论、 自相似(self-similarity)理论、 分形方法以及分形应用四方面构成。

(一)分形维数

分形是描述大自然和客观事物的一种新型几何语言， 弥补了欧几里得几何学的缺陷。分形维数是刻画图形占领空间规模和整体复杂性质的量度， 是图形最基本的不变量， 也是度量分形集复杂程度的一个量， 用于表示集合占有空间的大小。传统欧氏几何的维数都为整数， 描述简单而规则的人造物体； 而分形维数为包含整数的分数， 描述大自然大量不规则的欧氏几何无法描述的物体。

(二)自相似理论

分形自相似理论认为自然界存在的一切事物都具有自相似的层次结构， 局部与整体在形态、 功能、 信息、 时间、 空间等方面具有统计意义上的相似性， 这些局部与整体不完全相同， 又有某种相似的地方， 适当的放大或缩小几何尺寸， 整个结构不变。

(三)分形方法

分形方法是根据物体形态结构， 利用描述自相似性的数学功能来表现物体构成的拓扑结构及形态。建筑设计中实现分形建模的方法主要有三类：

一是基于维数在1～2之间的皮亚诺(Peano)、 科契(Koch)、 康托(Cantor)曲线等线性而简单的分形方法， 通过简洁易行的手工设计手段进行建筑立面造型设计和建筑界面纹理设计；

二是基于维数在2～3之间的谢尔宾斯基(Sierpinski)等分形方法进行建筑空间建构设计， 可以人工绘图设计， 亦可通过计算机辅助完成；

三是运用迭代函数系统(Iterated Function System和L-Systems)的计算机图形分形方法模拟建筑形体设计， 包括计算机仿生模拟。

以上典型方法通过若干次分形变换， 将空间元素的无限嵌套性源于设计过程的简单迭代， 复杂的建筑空间形体利用一个简单的图元， 通过一定规则的反复迭代生成， 从而产生不同尺度的细节， 形成极度丰富的建筑形体。

(四)分形应用

分形理论已被广泛应用到自然科学和社会科学的几乎所有领域， 包括计算机图形学、 数据处理、 物理、 化学、 生物学、 艺术设计、 服装设计以及城市规划、 建筑园林设计等领域。分形的建筑实践主要涉及自相似与尺度层级原理的应用， 以及直接利用各种分形方法通过计算机生成建筑窗格或平面图形， 在分形图形设计理论与方法上取得了很大的发展， 但这些图形存在建筑功能性与适用性较差的问题， 因此有待于将这些成果往建筑实用性方向转化与深化。

二、 分形美学与分形建筑美学

(一)分形美学

分形理论认为自然界存在的一切事物都是由不同层次的结构的集合， 这些不同层次结构具有无限的细节结构， 虽尺度不同， 却有着自相似的特点， 且在任意小的比例尺度内包含整体。所谓自相似， 指形式的递归， 在一个图形内还有相似的图形。自然界的一切事物存在着无穷的内在层次， 层次之间存在着“自相似性”或“不尽相似”， 放大或缩小几何尺寸， 整个结构并不改变， 分形美学展现在以下方面：

1. 自相似嵌套对称的分形美

它除了包含传统的上下、 左右及中心对称等观念之外， 其自相似性又揭示了一种新的对称性， 即局部与整体的对称。分形美学作品的局部图形与整体的图形是相似的(图1左)， 并具有无限精细的结构层次和层级嵌套性， 而无论是哪一个层次的局部都保持着整体的基本形， 以此获得整个图形的和谐和均衡。

2. 分形曲线的新内涵与丰度美

传统绘画和设计中， 线条主要有直线、 圆弧线、 波浪线， 在数学上这些线条大都是可微分的； 然而在分形美学中， 线条是十分复杂和不规则的， 常会使用皮亚诺曲线、 希尔伯特曲线、 柯赫曲线(图1中)等。尽管这些曲线十分复杂和奇异， 但成长它们的规则却十分简单， 无序中蕴涵着有序， 复杂中蕴涵着简单， 变化中蕴涵着丰度美。

3. 不规则自然美的属性

现代设计美学强调用简单的几何形体来获得明确和肯定的效果， 而分形美学是人们在自然界和社会实践中所遇到的不规则事物的一种数学抽象， 它研究的对象是自然界和非线性系统中出现的不规则物体的几何属性。

4. 奇异美学形式

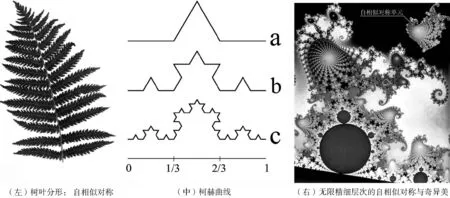
图1 分形美学图形来源: (左)与(右)图引自www.fractal.net.cn， (中)图作者自绘。

由于分形美学包含着精细的层层嵌套体系， 因而形式十分丰富， 给人以启迪和联想(图1右)。分形美都有一个共同的特征即没有特定尺度， 因为它具有每一种尺度， 当从不同的尺度和远近距离观看， 都能发现它的构造单元的变化， 从而获得新的感受。

(二)分形建筑美学及其意义

1. 分形建筑美学

分形建筑美学建立在建筑学和分形美学的基础上， 用分形理论研究建筑领域里的美和审美问题。分形建筑美学反映了建筑普遍存在的自相似规律， 并体现出许多传统美学的标准， 如对称性、 复杂性、 过程性和丰度性等， 但绝不是传统建筑美学的翻版， 而是对其发展、 突破和超越。

首先， 分形建筑美学揭示建筑嵌套自相似对称之美。这种对称除了包含建筑的轴线对称及中心对称观念以外， 其自相似性又揭示了一种建筑空间或形态的嵌套对称性， 即局部与整体的对称。城市与区域、 街区、 地段和建筑之间， 以及建筑局部空间形态(图形)与整体空间形态(图形)之间体现这种对称性(图2与图3)， 并具有一定数量、 嵌套的结构层次， 不同尺度的视觉感受各不相同， 而无论是哪一个空间层次的局部都保持着整体的基本形， 以此获得整个建筑空间的和谐和均衡， 展现出建筑的分形美， 这也是传统建筑美学所不具备的。

其次， 城市和建筑空间形态、 轮廓与边界之本质是分形曲线及其美学表现。分形建筑美学审视这种极度复杂的现象， 其描述方法具有意想不到的简单与规则性， 强力地表达分形图形美。在建筑领域里， 从城市到建筑直至其细部的若干层次中都广泛存在着分形现象， 而传统城市与建筑中表现得尤为突出： 城市及建筑的各种边界、 等高线和轮廓线等是十分复杂和不规则的， 用分形美学方法来衡量， 可以计算出其分维值， 且它们成长的规则却十分易于把握与控制， 展示无序中蕴涵着有序， 复杂中蕴涵着简单的分形美。这种美感是现代建筑美学所无法描述的。

第三， 建筑设计和建造过程的分形特征。建筑面对的是个复杂的系统， 尽管最后结果是有序和确定性的， 但是其成长历程处于不稳定、 非平衡和随机的状态之中， 是建筑师综合众多的功能、 技术、 安全、 人文与经济等设计和施工因素， 经由非线性的交叉作用与复杂的建造过程而完成。

第四， 建筑分形美学具有奇异美和人性化属性。建筑分形图案往往出乎人们的意料， 其新颖别致、 奇特多变的图案令人耳目一新， 具有强烈的奇异美感。建筑分形美学把建筑视为一个不同尺度层次的分形系统， 当人接近建筑时， 随着距离的不同， 要求存在不同且对应人体的细部尺度， 建筑才具有吸引力、 趣味性和丰满度， 否则， 建筑会枯燥无味。分形将人与建筑空间细部尺度建立起关联， 为人们提供了满足人体尺度需要的尺度层级系统。

最后， 分形建筑美学是一种理性的建筑设计与评价方法。在建筑设计中， 分形美学提供了一种混合确定性和非确定性的量化工具， 可以利用分形理论生成复杂的韵律， 使建筑与周围环境取得协调， 从而建筑更加贴近自然和人性； 另一方面借助建筑分形美学可以对建筑进行量化的评判， 为评价建筑提供了更科学的标准。

2. 美学意义

作为一种方法论和认识论， 分形建筑美学不仅在理论上， 而且在实际应用上都具有重要的价值。首先， 其自相似性启发建筑师通过设计建筑局部进而扩展到建筑整体直至人居环境， 并能从嵌套属性和人性化尺度中扩展建筑设计层次和丰度； 其次， 分形建筑设计本身是科学的理性和艺术的感受完美的融合， 是数学和建筑艺术的统一， 并能给人以极大艺术震撼； 第三， 建筑设计艺术的进步有赖于设计手段的革新， 而分形建筑设计方法恰好为其提供了前所未有的艺术手段。

分形是建筑学一种强有力的工具， 一方面它可以作为一个有力的建筑批评工具， 有助于解释为什么许多现代建筑不能够被大众接受的原因——它们过于贫瘠； 另一方面， 在建筑设计中可以利用分形几何生成复杂的韵律， 并且使建筑与周围环境取得协调。[3]借助于分形方法， 可以把不同建筑直接进行同尺度下量化比较并评价， 或者与目前较好的建筑、 规

划实例进行横向或纵向、 同尺度或不同尺度下的分形对比， 对设计的多重合理性进行深入的评价。

三、 分形建筑审美

(一)自相似分形建筑美学展现

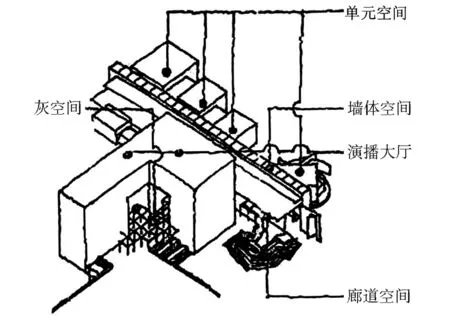
图2 高层建筑形式的自相似来源: 余斡寒， 汤桦. 纯净与变异——福建广播电视中心设计方案释义. 建筑师95期： 44—49.

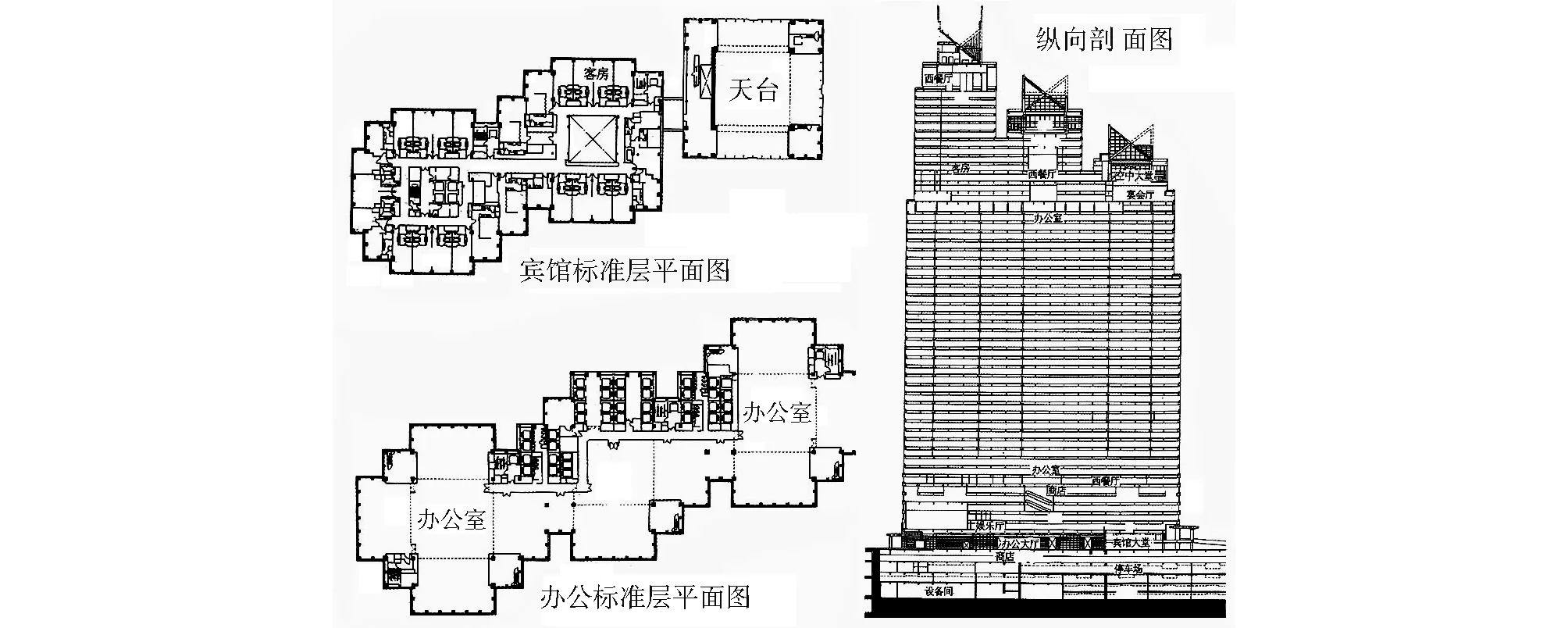
图3 高层建筑空间的自相似来源: 陈一峰， 陈纲， 卢峰编译. 世界高层建筑. 北京： 中国计划出版社， 2000. (日本新缩公园大厦)

建筑分形无处不在， 其空间所体现的分形美简单明了， 正是其复杂性展开的依据。从形式上审视， 建筑各组成部分之间不仅外形上具有自相似的美学特征， 而且各构成部分内部也存在嵌套关系的自相似， 图2所示的单元空间、 墙体空间和演播大厅等不仅外形上就是自相似几何体， 各自内部构成上也是嵌套的自相似几何体； 从空间构成分析， 当建筑开始以某种简单的公式组织自身， 譬如说各种基本功能的“元空间”按照走道式、 穿套式、 大厅式或单元式的组合原则构成各种尺度的组合空间， 并处处以无限的耐心重复着同样的法则时， 相似性和简单规则性的叠加组合就演绎出建筑空间的复杂性， 这就是建筑空间分形美学的具体表现。以高层旅馆综合体为例(图3)， 客房空间和卫生间构成单个旅馆客房单元(元空间)， 若干客房单元的组合及其与交通、 服务等单元的组合构成标准层空间， 各标准层的垂直叠加构成旅馆区， 旅馆区再与办公区、 交通服务等其它分区构成建筑空间整体； 尔后还可以与其它建筑形成城市的地段空间， 各地段空间组合形成城市街区， 城市街区之间的组合形成城市空间……， 在整个空间建构过程之中， 各个层次的空间结构具有自相似性并构成嵌套关系。

自相似的分形建筑之美揭示了其复杂空间构成本质上蕴涵的简单性。就像自然分形一样， 随着自然界从低级到高级、 从简单到复杂的进化， 终于产生了极其复杂的人类； 而用分形美学的观点来倒推， 自然的复杂缘自于重复的简单， 而且是惊人的相似性和简单性。如树枝的分形图(图4右上)看起来十分复杂和奇异， 但用计算机模拟成长它们的规则却十分简单， 复杂中蕴涵着简单。东京Tod's Omotesando大楼立面造型(图4)仿树枝分形， 体现大自然的鬼斧神工之美， 给人耳目一新之感。动物体内血管或植物树枝或养分输送系统呈现出一种分形美， 它们占用最小的面积、 以最高的效能而服务于整个生物体。分形美学启迪建筑师， 建筑、 城市同样能反映自然分形的效能美， 最小的辅助空间(包括最便捷的交通)服务于最大的使用空间， 仅仅这一点， 仿生建筑分形就有广阔的研究和运用前景。

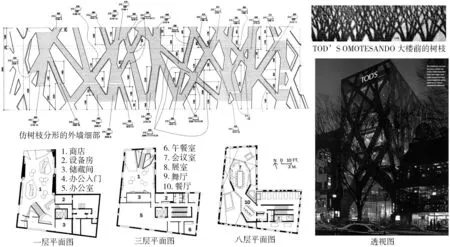
图4 东京Tod’s Omotesando大楼来源: Naomi R. Pollock. Toyo Tto fuses structure and wrapper in a network of concrete trees at the new Tod’s Omotesando Building in Tokyo. Architectural Record 2005(6): 78-85.

(二)递归尺度层级的建筑分形

建筑各部分之间以及与其它建筑、 环境之间存在一种不同尺度的嵌套关系和相似性的递归变化， 不仅是自相似的分形美学价值的体现， 也是尺度层级(hierarchy of scales)的分形美学表达。它满足了人们不同距离需要不同尺度的人性化需求， 使建筑更加贴近自然和人性； 尺度层级也是自相似展开的基础， 使重复和复杂的建筑空间和构件在不同的比例层次上展开和排列， 建筑整体性和秩序性才能实现； 此外， 尺度层级也是建筑各部分之间及其与环境协调和谐的本质所在。

分形建筑美学认为建筑随着观赏距离的变换应该具有对应的建筑尺度， 不同尺度层级、 连续的韵律是人性化建筑美学的具体表现： 建筑是一个不同尺度层级的分形系统， 它以人体基本尺度为依据， 当一个人接近或进入一栋建筑时， 随着距离的不同， 总是存在着一个嵌套的、 适合人的建筑细部， 表达出其对应性、 层级性和人性的分形之美。因此， 建筑、 规划设计的成功与否与体验其过程的尺度层次有关， 细部决定成败， 有趣的细部表达了整体的创作意图， 否则， 建筑会枯燥无味。图5巴林马拉马联合海湾银行随着观赏距离的不同， 展现与之相适应的建筑细部层次， 充分表达了建筑递归尺度层级的分形美学意义。

图5 高层建筑尺度层级的分形美学价值来源: 汪丽君， 钟声， 舒平. SOM事务所. 北京： 中国建筑工业出版社， 2004： 74-79.

(三)镶嵌韵律的建筑分形

基于不同的尺度层级， 建筑形式和空间构成都充斥着嵌套的、 自相似的对称韵律之美。镶嵌图案很早就运用于建筑之中， 中国传统建筑的窗格和藻井、 古罗马建筑的马赛克、 伊斯兰建筑的镶边等， 都包涵着大量镶嵌图案信息， 空间更是广泛存在镶嵌关系。

建筑的镶嵌韵律是由单个图形和空间重复或叠加而成， 具有极强的相似性和规律性。微观上看， 每一个单位图形还可以简化为一个几何图案或数个几何图案的组合， 体现在建筑当中， 则是建筑单元空间或构图在空间或平面上继续细分， 每一次细分都与上、 下层次的空间或图形存在包络关系， 即上层次包络下层次； 宏观上看， 单元空间或几何图案的边界形成了建筑的控制网格， 每一个网格代表一个单元空间或单元图形， 它们的并置叠加就形成自相似的复杂图形， 并构成宏观层次的嵌套关系， 通常嵌套关系都表现为正交、 斜交或圆形控制的网格形式， 由于形式常见， 因而不会引起人们的兴趣， 而事实上， 分形之美就环绕在人们的居住的建筑之中。

(四)建筑天际线的分形审美

建筑轮廓及其所构筑的城市天际线就展现了丰富的分形美学特点。一方面， 不同时期的建筑的轮廓表现出不同的分形美学特征， 分维值从小到大， 建筑轮廓由简洁到复杂， 由纯净到丰富， 形成某一确定的分维值， 构成建筑空间形态的可识别性， 传达不同分形美学价值和特征； 另一方面， 建筑轮廓分形还表现在它们之间的非线性组合构筑了极其复杂的城市天际线， 城市天际线自然也就会带有与建筑轮廓线自相似的特性， 反映出分形曲线“形态复杂而原理简单”的分形美学特征， 并构成了城市空间形态的标识性。

用1和2之间的分维值可以描述城市和建筑边界的复杂程度， 用2和3之间的分维值可以描述城市建筑空间的紧凑度， 建筑、 城市在不同尺度下的轮廓线也可以计算出其分维值， 它反映城市和建筑的尺度层级和细部级数。分形维数可以描述建筑反映在视觉上的复杂性， 因而也为建筑形式的丰富程度提供了一种量化的办法。“国际风格”和“后现代风格”的建筑分形美学特征非常明显， 如图6(左)美国旧金山泛美大厦的分形数值相对较小， 建筑轮廓简单； 图6(中)美国纽约南渡口广场大厦分形数值相对较大， 建筑轮廓丰富， 而且相似类型与风格的建筑轮廓线都呈现出不同的分形曲线特征， 但其分维值也保持相对稳定的范围。从自由女神像一侧拍摄的20世纪末曼哈顿区全景， 其计盒维数是1.56， 而在大多数郊区住宅区， 轮廓线的计盒维数大约在1.1-1.3之间。[14]再比较18、 19和20世纪纽约城市天际线图(图6(右))， 显而易见， 18世纪城市高层建筑较少， 城市轮廓线跌宕起伏小， 简单而贫瘠， 分维值最小； 20世纪城市高层和超高层建筑大大改观了城市轮廓的起伏节奏和韵律， 跌落对比强烈， 轮廓线复杂而丰富， 分维值最大； 而19世纪城市天际线分形特征介于18和20世纪之间。

图6 高层建筑轮廓的分形美学价值来源: 雷春浓. 高层建筑设计手册. 北京: 中国建筑工业出版社, 2002.

(五)分形的建筑文化展现

建筑空间与文化的演变具有相同的尺度层级和一致性， 是极其重要的分形美学表现。文化的演进也存在迭代现象， 这就是文化传播中的分形。某种场地文化或价值取向被吸收、 溶进特定的城市或建筑环境中， 并经过该场地环境的创造而得以弘扬， 就是文化的分形迭代， 各种隐含的、 深层次的文化现象会被沉淀， 并延续下来。

马来西亚皮特纳斯双塔大厦以其独特的伊斯兰教艺术建筑文化与当代建筑科技完美融合， 而成为吉隆坡的跨世纪的标志。塔楼的形状从伊斯兰教传统中吸取灵感， 从伊斯兰教艺术中吸取特色而设计的， 在伊斯兰教传统中， 几何图形所具有的象征性要比西方文化更重要。[15]

Cesar Pelli & Associates建筑设计公司在研究了传统的伊斯兰图案花纹后得出一种八角星， 那是由两个正方形旋转以后再叠加形成的， 而这正是建筑平面形式与民族文化构成分形， 表达伊斯兰文化价值。由于八角星造成了楼层布局不合理， 外墙内转角离大厦核心太近， 从而影响了楼面使用上的灵活性， 其后进行了不尽相似的拓扑变换， 在八角星的8个内角迭加8个半圆形， 从而形成了一种有16个分枝的形状(图7)。

随着每座塔楼的上升， 它们向内收缩形成锥度， 外墙也缓慢地向中央倾斜， 完成了大厦的锥度造型， 在视觉上增强了摩天大楼的中轴垂直线。双塔上添加了小尖塔， 一种明显的马来西亚楼顶， 与摩天大楼或教堂的尖顶迥然不同。吉隆坡皮特纳斯双塔大厦表达了马来西亚伊斯兰传统文化符号， 充满个性， 建筑与文化珠联璧合， 是一种建筑文化分形的美学展现。

四、 分形美学——一种科学理性的设计与评价方法

分形建筑美学是探讨建筑与城市科学的重要美学观， 与系统论互补， 揭示了建筑与环境多层面、 多视角、 多维度的联系方式。首先， 分形的自相似和尺度层级理论建立起各种设计关联， 为建筑设计提供了更科学的思维理念， 并作为建筑设计的依据和手段， 使建筑更加贴近自然、 环境和人性； 其次， 通过简单的分形分析或计算， 可以对建筑与环境、 经典作品、 自然生成物之间进行分形比较， 以此借鉴优秀设计的精髓， 并可以使建筑与环境和谐统一； 此外， 对建筑尺度层级的连续性进行分析， 可以判断建筑的丰度性与自然属性， 依据尺度层级的缺失判断建筑的合理性， 这些为建筑设计评价提供了较为理性的科学依据。

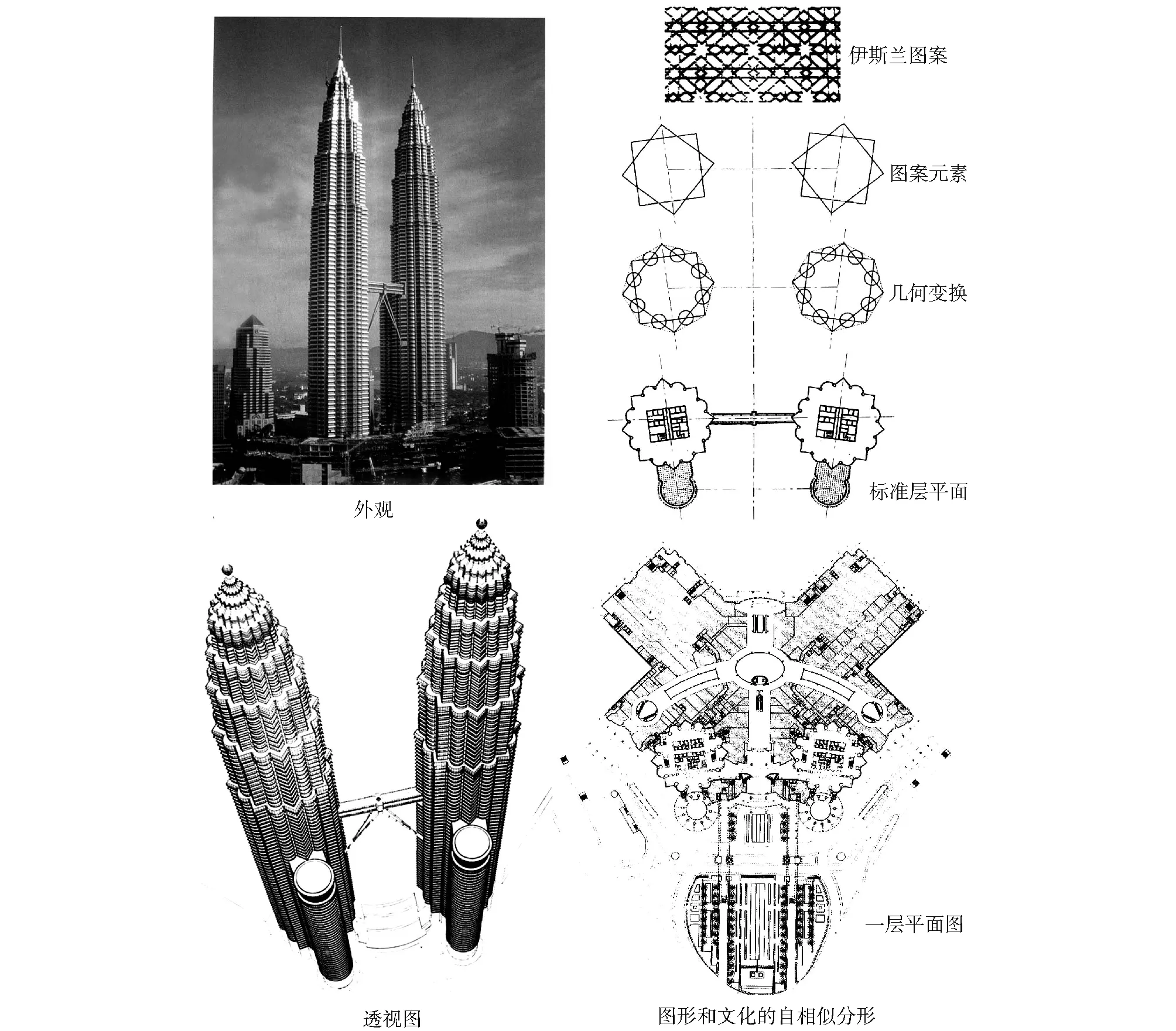
图7 马来西亚吉隆坡皮特纳斯双塔大厦来源： Francisco Asensio Cerver. New Architecture eleven——Recent Works. Barcelona (Spain): Arco editorial, s.a. 1997.

参考文献：

[1] (法)曼德布罗特. 分形： 形式、 机遇和维数 [M]. 文志英， 苏虹， 译. 北京： 世界图书出版社， 1999.

[2] M Batty， P Longley. Fractal Cities: A Geometry of Form and Function [M]. London: Academic Press， 1994.

[3] Bovill Carl. Fractal Geometry in Architectures and design [M]. Boston： Cambridge, press, 1996: 1-191.

[4] 李得仁, 廖凯. 从混沌分形看中国古典建筑与园林设计 [J]. 武汉测绘科技大学学报, 1998(3): 189-193.

[5] 李世芬， 赵远鹏. 空间维度的扩展——分形几何在建筑领域的应用 [J]. 新建筑， 2003(2)： 55-57.

[6] Nikos A Salingaros. Architecture， Patterns and Mathematies [J]. NNJ, 1999(2): 4-8.

[7] Nikos A Salingaros. The Laws of Architecture from a Physicist's Perspective[J]. Physics Essays， 1995 (8): 15-22.

[8] Wolfgang E Lorenz. Fractals and Fractal Architecture[EB/OL]. (2004-07-16) [2008-07-27]. http: //www. welo. at/ welo-research/master-thesis. html.

[9] 赵远鹏. 分形几何在建筑中的应用 [D]. 大连： 大连理工大学建筑与艺术学院， 2003.

[10] 于雅琴. 分形建筑设计方法研究 [D]. 大连： 大连理工大学建筑与艺术学院， 2008.

[11] 冒亚龙， 雷春浓. 一种理性的建筑设计与评价视角——应用分形的建筑设计尝试 [J]. 重庆建筑大学学报, 2005(4)： 4-9.

[12] A Crompton. The Fractal Nature of the Everyday Environment [J]. Environment and PlanningB: Planning and Design, 2007(2): 243-254.

[13] Sala N. Fractal geometry and architecture: Some interesting connections [J]. WIT Transactions on the Built Environment, 2006(2): 163-173.

[14] M Batty， P Longley. The Fractal City (abstract) [J]. Architectural Design， 1997 (10)： 5-53.

[15] Francisco Asensio Cerver. New Architecture eleven——recent works [M]. Barcelona (Spain): Arco editorial S A， 1997.