基于模糊熵层次分析法的高等教育国际化策略风险评价模型研究*

胡亦武

(华南理工大学 国际交流与合作处， 广东 广州 510640)

一、 引言

高等教育国际化是一项复杂的社会系统工程， 要在教育内容、 教育方法上适应国际交往和发展的需要， 培养有国际意识、 国际交往能力、 国际竞争能力的人才[1]。多年来， 中国大学主要在课程和教学、 师资队伍、 人才培养模式、 组织结构、 科研开发等方面的国际化进行了全面探索[2-3]。但如何建立中国大学国际化长期有效的动力机制， 如何评价中国大学国际化的程度， 如何全面剖析大学国际化影响因素， 如何评估高等教育国际化策略的投入风险[4]， 等等， 需要采用系统工程的理论和方法来研究其评估和决策问题。

由美国匹兹堡大学教授T. L. Saaty于20世纪70年代提出的层次分析法(Analytic Hierarchy Process, AHP)是一种多准则决策方法， 广泛应用于复杂系统的分析与决策[5]。利用AHP或者对其进行相应改进[6-11]， 可以实现对中国大学国际化策略投入风险的定性分析和定量分析， 但AHP在方案两两比较重要性赋值时只考虑了个人判断的两种可能极端情况， 而没有考虑个人判断的模糊性， 同时， 如果采用平均值进行指标量化， 可能会导致有用信息的丢失， 为此， 本文采用模糊熵理论在构造模糊一致性判断矩阵和计算指标权重基础上提出了基于模糊熵层次法的中国大学国际化策略风险评价模型。根据模型对策略的综合评估值得出风险等级， 从而为相关决策的制定提供重要依据。

二、 高等教育国际化策略的风险要素

在不同层面实施大学国际化策略时， 考虑到中国大学国际化投入对社会的整体发展具有较大的推动作用， 如果有限的中国大学教育资源被浪费或产生风险， 势必影响实现中国大学教育“规模、 结构、 质量、 效益相统一”的发展方针[1]。伴随着中国大学国际化的发展， 中国大学国际化投入的经济效益和社会效益倍受中国大学教育管理部门关注。 高等教育国际化已成为新的机遇性挑战， 如何评价由此带来的风险， 具有重要的意义和价值。中国大学国际化策略风险量化旨在通过对风险相互作用的评估来评价项目的投入风险等级， 从而确定该项目的可行性和价值。

从政治、 文化、 学术、 经济和人力资本等因素， 根据专家调查问卷和相关文献资料[12-16]， 利用SPSS软件对指标进行相关性分析， 本文选取了七个影响教育国际化策略的风险要素： 高等教育国际化政策风险、 国际化发展规划设计与实施风险、 合作办学的风险、 学生国际交流的风险、 引进国外人才和培养师资队伍的风险、 国际学术交流与合作的风险、 面向国际化的教学改革的风险。每一个要素又具有相应的二级子要素。高等教育国际化策略风险评价指标体系表示为如图1所示的分层结构。

图1 高等教育国际化策略风险评价指标体系

三、 基于模糊熵层次分析方法的模型

建立中国大学国际化策略风险评估指标体系是进行中国大学国际化策略风险评估的基础。采用层次分析法进行指标综合， 涉及了许多定性的评价指标， 各指标的权重作为评价体系的基本参数， 其确定过程中必须对定性资料进行处理。常用的模糊综合评价方法在量化过程中， 选择的往往是平均数， 因而会使许多有用的信息丢失， 为弥补这一不足， 考虑所研究问题的特点本文采用钟形曲线隶属度函数对定性指标进行模糊量化处理。此外， 鉴于评价指标对于被调查者或评估人员的难易程度不同或者对其重视程度不同， 往往使得对于某一指标的调查结果相对分散， 为了将此项信息反映到评价体系中去， 结合熵评价的思路对指标权重进行了修正。

(一)钟形模糊隶属函数的确定

根据本文研究数据的特点， 采用钟形隶属度函数作为变量模糊化函数。具体定义为： 设一个模糊量由(a,b,c)决定， 且具有钟形隶属度函数：

(1)

式中，a表示模糊量的偏差系数， 反映了该模糊量的数值发散幅度；b表示模糊量的变化梯度， 反映了该模糊量的准确程度， 为了保证μA(x)为实数， 参数b为b≥1的正整数；c表示了模糊量最大可能的取值， 决定了该模糊量数值变化范围的中心值。其中μA(c-a)=0.5，μA(c+a)=0.5和μA(c)=1。

则称模糊量为钟形模糊量， 其分布如图2所示。

图2 钟形模糊量分布曲线

通过调整a和c， 可以改变钟形隶属度函数的中心和宽度； 通过改变参数b值可以调整钟形模糊隶属度函数斜边的斜率。

采用钟形曲线隶属度来确定测评指标的权重主要过程如下：

1. 建立专家初始评价矩阵

设有n个专家参与评价模型的确定， 评价指标共有p个， 由第j个专家对第i个指标给出评价[aij，bij，cij]。aij表示第j个专家对第i个指标重要程度给出的最保守的评价，bij表示第j个专家对第i个指标重要程度给出的最可能的评价，cij表示第j个专家对指第i个指标重要程度给出的最乐观的评价。要求专家在[0， 100]间自由打分， 从而形成初始评价矩阵R：

(2)

2. 建立专家评价的权重集

设第j个专家给出的评价值在总体评价中所占的比重为cj， 从而组成专家评价的权重集：

E=[e1…ep]

(3)

3. 模糊合成

利用E⊙R表示专家重要性和评价值的模糊合成结果， “⊙”为模糊合成算子， 其具体运算有多种， 如M(∧, ∨)算子、M(·, ∨)算子、M(∧, ⊕)算子、M(·, ⊕)算子等， 其中加权平均型模糊算子在M(·， ⊕)体现权系数作用、 综合程度和利用R的信息方面都有优势， 因此采用该算子进行模糊合成， 从而形成模糊合成矩阵：

F=[[a1b1c1] … [anbncn]]

4. 确定模糊权重

根据钟形模糊量计算公式， 第i个指标的模糊权重为：

(5)

并经过归一化处理后得到模糊权重集：

Wτ=[τ1τ2…τp]

(6)

(二)熵权的确定

高等教育国际化策略风险评价主要依据专家定性评价的指标， 而指标本身之间的属性和特点不同， 这就使得搜集到的不同指标的信息质量不尽相同。因此， 需要引入熵评价的方法， 依据信息质量对指标权重进行调整。

1. 模糊熵理论

模糊事件A的熵定义为：

(7)

式中，A为{x1，x2， …，xn}中的模糊事件，μA(xi)、Pi分别是模糊事件xi的模糊隶属度和概率密度。

基于以上定义的基础上， 高等教育国际化策略风险模糊熵评价模型可表示为：

(8)

当α=1时， 高等教育国际化策略风险中模糊事件A的广义熵就变为模糊事件A的熵定义； 当α=0.5时， 高等教育国际化策略风险中模糊事件A的广义熵就变为概率不确定性的熵定义； 当α=0时， 高等教育国际化策略风险中模糊事件A的广义熵就变为模糊补事件的模糊熵定义。

2. 指标总熵

在钟形隶属度函数模糊矩阵R的基础上， 确定第i个指标的总熵为

(9)

式中，a,b,c,n表示的意义如以上所述， 计算量r在评价指标矩阵[aij,bij,cij]中取值。

3. 指标熵权的确定

在指标总熵计算式的基础上， 计算第i个指标熵权为：

(10)

从而得到熵权集：

Wρ=[ρ1,ρ2, …,ρp]

(11)

(三)组合权重的确定

设WA=[β1,β2, …,βp]是通过层次分析法确定的层次权重集。

为了能够综合模糊权、 熵权和层次分析权重， 利用式(12)进行多个权重的综合。最后获得第i个指标包含模糊熵的最终调整权重为：

(12)

从而得到最终权重集：

W=[w1w2…wp]

(13)

通过式(12)获得组合权重能够确保评价指标即考虑了指标的定性和定量问题。同时， 各指标值所反映的信息并不是有序和有规律的， 所以利用熵理论将专家对指标的评价信息进行量化， 可以将无序的信息变成有序可比的信息， 从而对最终权重进行校正。

四、 高等教育国际化策略的风险评价模型

根据对高等教育国际化策略风险的分析， 可以得到图1所示的指标体系。策略风险评价主要步骤如下：

(一)确定各指标因素及其权重

确定评价指标因素作为模型输入， 然后根据专家对各项指标重要性的调查结果， 建立初始评价矩阵， 根据式(2)至式(13)确定模糊权重、 熵权和层次权重， 以及组合权重。专家对各指标的初始评价矩阵如表1所示。

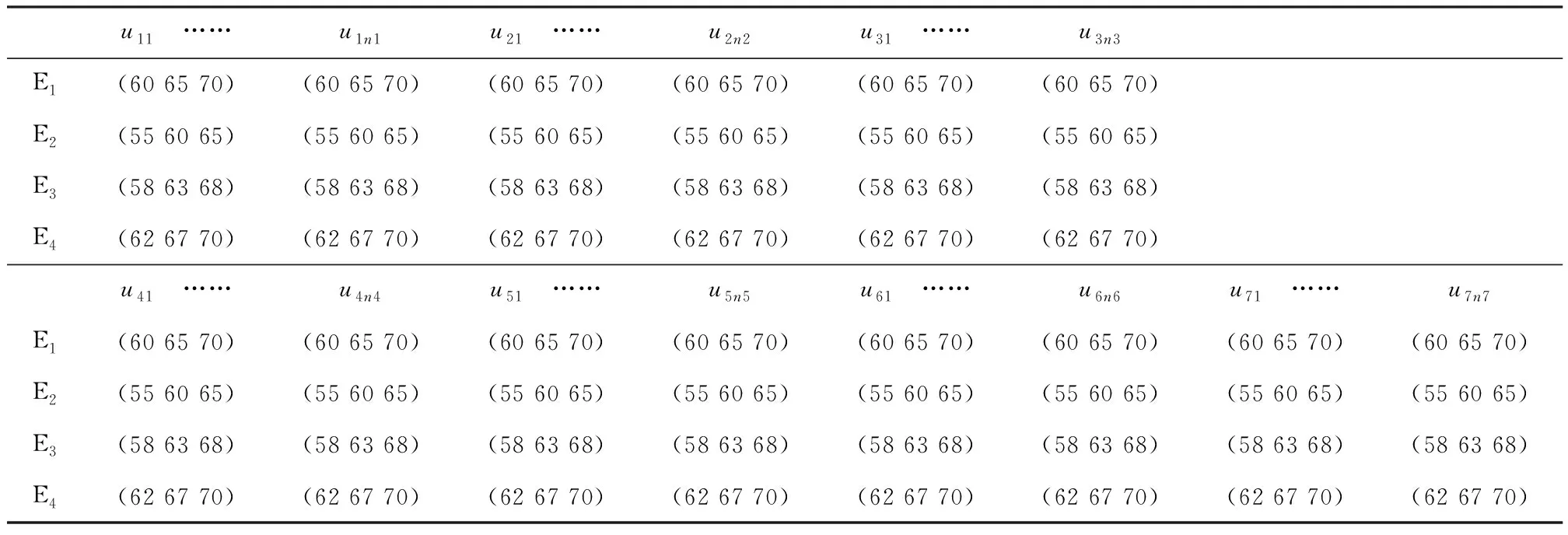
表1 专家初始评价矩阵

(二)建立指标值的模糊判断矩阵

通常， 在调查问卷的设计中采用五级记分制， 如表2所示， 因此， 调查获得的指标值是一个模糊判断矩阵。目前， 常用的隶属函数确定方式有： 通过模糊统计； 采用二元对比排序法； 借用常用的模糊分布； 利用信号处理的结果， 经过适当转换得到隶属函数； 通过神经网络模型来学习和获取隶属函数； 其他方法。如主观认识， 个人经验， 人为评分等。 根据策略风险状况采用以上方式建立以下某层个指标值个风险等级的模糊判断矩阵为：

(14)

式中，μij是风险的隶属度， 0≤i≤p， 0≤j≤n。

(三)求各指标评价矩阵

根据上面方法求得的各指标权重和模糊判断矩阵， 各指标评价矩阵进行归一化和综合后可表示为：

(15)

式中， 0≤i≤p,T表示转置。

(四)建立目标价矩阵

目标价矩阵可表示为：

Bobj=[B1B2…Bp]

(16)

(五)模糊综合评价

进行模糊综合评价， 得到模糊综合评价结果集， 即权重向量W与模糊矩阵B的合成所得的模糊子集S为：

S=W·B

(17)

其中W为综合权重值，S为大学国际化策略风险模糊评估结果子集。

(六)确定大学国际化投入风险水平值

中国大学国际化投入项目的风险评估值可表示为：

f=S·XT

(18)

式中，T表示转置矩阵；X为评价集中对应的分数向量， 评分表如表2所示。

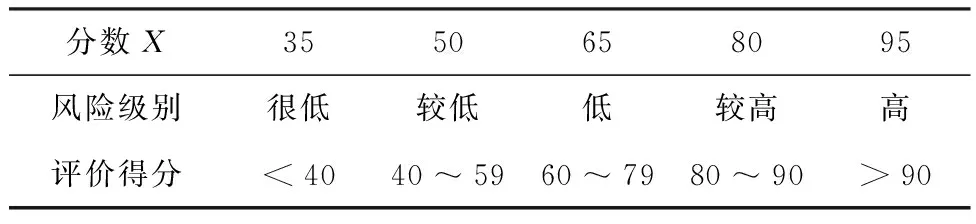
表2 中国大学国际化投入项目风险评分表

五、 实证分析

中国南方某大学进行了相关国际化项目的建设， 对整个项目进行了跟踪调查， 选取了4组投入指标进行策略风险评估包括{管理者认知能力风险(V11)、 管理能力风险(V12)、 投资目标的多项和漏项风险(V13)、 急于求成风险(V14)}、 {能否公平竞争(V21)、 承担义务的风险(V22)、 组织协调及各部门配合不确定性风险(V23)、 资金实力的风险(V24)、 管理工作者带资和垫资的风险(V25)、 资金信誉情况(V26)}、 {被教育者需求不确定性风险(V31)、 国际化市场接受不确定性风险(V32)、 市场竞争不确定性风险(V33)}、 {政策风险(V41)、 经济风险(V42)、 自然条件风险(V43)}， 根据各因素调查结果， 采用模糊熵权重方法确定权重， 经计算可得分层权重集为：

W=[W1,W2,W3,W4]=[0.23, 0.25, 0.30, 0.22]，

W1=[W11,W12,W13,W14]=[0.36, 0.20, 0.20, 0.24]，

W2=[W21,W22,W23,W24，W25，W26]=[0.25, 0.16, 0.18, 0.16, 0.18, 0.07]，

W3=[W31,W32,W33]=[0.40, 0.20, 0.40]，

W4=[W41,W42,W43]=[0.36, 0.40, 0.24]。

根据实际情况， 采用最大信息熵原理确定中国大学国际化投入风险模糊隶属函数， 并根据调查结果建立如表3所示的中国大学某国际化项目投入风险模糊评判表。

表3 中国大学某国际化项目投入风险模糊评判表

由表3可知中国大学某国际化项目投入风险指标模糊判断矩阵Ri为：

归一化处理后的各因素评价矩阵Bi为：

B1=(0.3294， 0.4157， 0.1765， 0.0784， 0)；

B2=(0.1692， 0.436， 0.2505， 0.1098， 0.0346)；

B3=( 0.3107， 0.3883， 0.233， 0.068， 0)；

B4=(0.2303， 0.2718， 0.2075， 0.2282， 0.0622)；

模糊综合评价结果集S=W·B=(0.2619， 0.3809， 0.2188， 0.1161， 0.0223)；

中国大学某国际化项目投入风险评价值为：f=S·XT=(0.2619， 0.3809， 0.2188， 0.1161， 0.0223)×(35， 50， 65， 80， 95)T=53.84。

对照表2可知， 该大学的国际化项目投入风险级别为较低。

六、 结论

本文提出了基于模糊熵层次法的中国大学国际化策略风险评价模型。运用该模型对中国大学国际化投入项目风险进行量化， 只需要项目有关人员和专家给出风险因素的评价信息和两两比较判断信息即可， 可操作性强。

中国大学国际化投入风险评价结果正确与否， 很大程度上取决于能够科学、 客观、 综合地反映评价对象整体状况的指标内容、 结构及评价的标准。中国大学国际化投入风险的问题涉及许多方面， 因而在实际运用中， 建议中国大学国际化管理部门选取适当因素建立数据库， 开发相应的中国大学国际化投入风险评价软件。在实际的评价过程中还可以引入系数， 对不同类型的中国大学国际化投入进行修正。

参考文献：

[1] 蒋凯， 马万华， 陈学飞. 应对国际化的挑战： 大学战略规划与战略管理 [J]. 北京大学教育评论， 2007(1)： 177-179.

[2] 黄蔚， 杨晨光. 高等教育国际化进程中大学如何制定发展战略——第二届中外大学校长论坛侧记 [J]. 教育研究， 2004(10)： 92-96.

[3] 李晨. 高等教育国际化背景下的中外合作办学研究 [D]. 青岛： 青岛大学教育经济与管理， 2007.

[4] 张寿松. 高等教育国际化的十个基本问题 [J]. 大学教育科学， 2003(03)： 15-19.

[5] 黄贯虹. 系统工程方法与应用(修订版) [M]. 广州： 暨南大学出版社， 2006.

[6] 孔繁森， 王军， 孙海港. 基于层次分析法的发动机缸体生产线设备可用性的模糊综合评价 [J]. 吉林大学学报(工学版)， 2008(6)： 1332-1336.

[7] 段秉乾， 司春林. 基于模糊层次分析法的产品创新风险评估模型 [J]. 同济大学学报(自然科学版)， 2008(7)： 1002-1005.

[8] Stamatelatos M. Probabilistic risk assessment procedures guide for NASA managers and practitioners[R]. Washington D C： Office of Safety and Mission Assurance NASA Headquarters, 2002.

[9] Sen D K, Banks J C, Maggio G, et al. Rapid development of an event tree modeling tool using COTS software[R]. New Jersey: IEEE Aerospace Conference,2006.

[10] Epstein S, Rauzy A. Can we trust PRA [J]. Reliability Engineering and System Safety, 2005(3): 195.

[11] JIA Yue, SONG Bao-wei, ZHAO Xiang-tao, LIANG Qing-wei. Method of Combat Programs Optimization by Fuzzy AHP Based on Entropy Weight [J]. 系统仿真学报， 2008(11)： 2965-2968.

[12] 刘广明. 论教育国际化和我国高等教育的应对策略 [J]. 河南师范大学学报(哲学社会科学版). 2003(6)： 133-135.

[13] 徐海宁. 高等教育国际化的多视角分析 [J]. 江苏高教， 2006(2)： 51-53.

[14] 夏辽源. 我国高等教育国际化问题研究 [D]. 长春： 东北师范大学教育学原理， 2006.

[15] 宋扬. 高等教育国际化的研究——兼谈我国高等教育国际化的对策 [D]. 上海： 华东师范大学教育经济与管理， 2002.

[16] 鄂加强. 智能故障诊断及其应用 [M]. 长沙： 湖南大学出版社， 2006.