一维AB结构的电磁特异材料的有效媒质参量确定

邓文华， 蒋练军*， 邓跃龙， 万小军

(1.湖南城市学院物理与电子信息工程系，中国 益阳 413000；2.益阳医学高等专科学校公共课部，中国 益阳 413000)

电磁特异材料是由一些人工制备的电磁共振单元组成，当探测电磁波的波长远大于组成单元的晶格常数时，特异材料可以被看作是一种均匀的有效媒质，它具有等效介电常数和磁导率，这就是有效媒质的概念[1]．当人们制备出了特异材料样品后，它是否可以被等效为有效媒质，如果可以等效的话如何计算其有效的介电常数εeff和磁导率μeff，这些都是特异材料的研究中非常基本和重要的问题． 对于如何计算体系的等效介电参量，Pendry在1996年提出的金属线立方格子结构，其有效的介电常数εeff是利用等效近似的方法得出的经验公式[2]；另一类方法是通过对特异材料体系内非均匀的局域场做积分平均的方法来定义体系的有效媒质[3,4]；另外有人提出了等效回路模型来计算体系的有效媒质[5-7]．严格来说，这些方法都是一些近似理论. 其近似的程度有多大，成立范围是什么，这些都值得进一步探讨．计算体系的有效媒质参量，有一种大家熟知的方法，就是利用特异材料的透射和反射信息来求解体系的等效介电参量，因为它包含了体系的折射率和阻抗的信息，可以通过反解的方法求得，这就是S参量反解方法[8-9]．尽管人们已经提出了很多有效的媒质理论和计算方法，它们也在不同方面获得了巨大成功，但是传统方法仍然存在一些问题．例如，S参量反解法存在解非唯一的问题；在有些情况下，当真空中的波长大于特异材料的晶格常数时，即满足长波近似条件，体系依然不能被等效为有效媒质[10]；有的时候从薄的特异材料体系计算出的有效媒质不能适用于厚的体系[11-12]，这个现象非常奇怪，因为体系的有效介电性质应该是其局域特性，并不应该依赖于体系的厚度．面对这些问题，我们觉得非常有必要进一步探讨体系的有效媒质参量的计算方法，本文基于推广的相干势近似(Generalized Coherent Potential Approximation，简称GCPA)的方法[13]，采用研究特异材料有效媒质性质的“准模”方法，将特异材料放入背景材料中，利用格林函数的方法来计算一维AB结构的电磁特异材料体系的自能，态密度，从而确定体系的有效媒质性质．

1 物理模型与理论基础

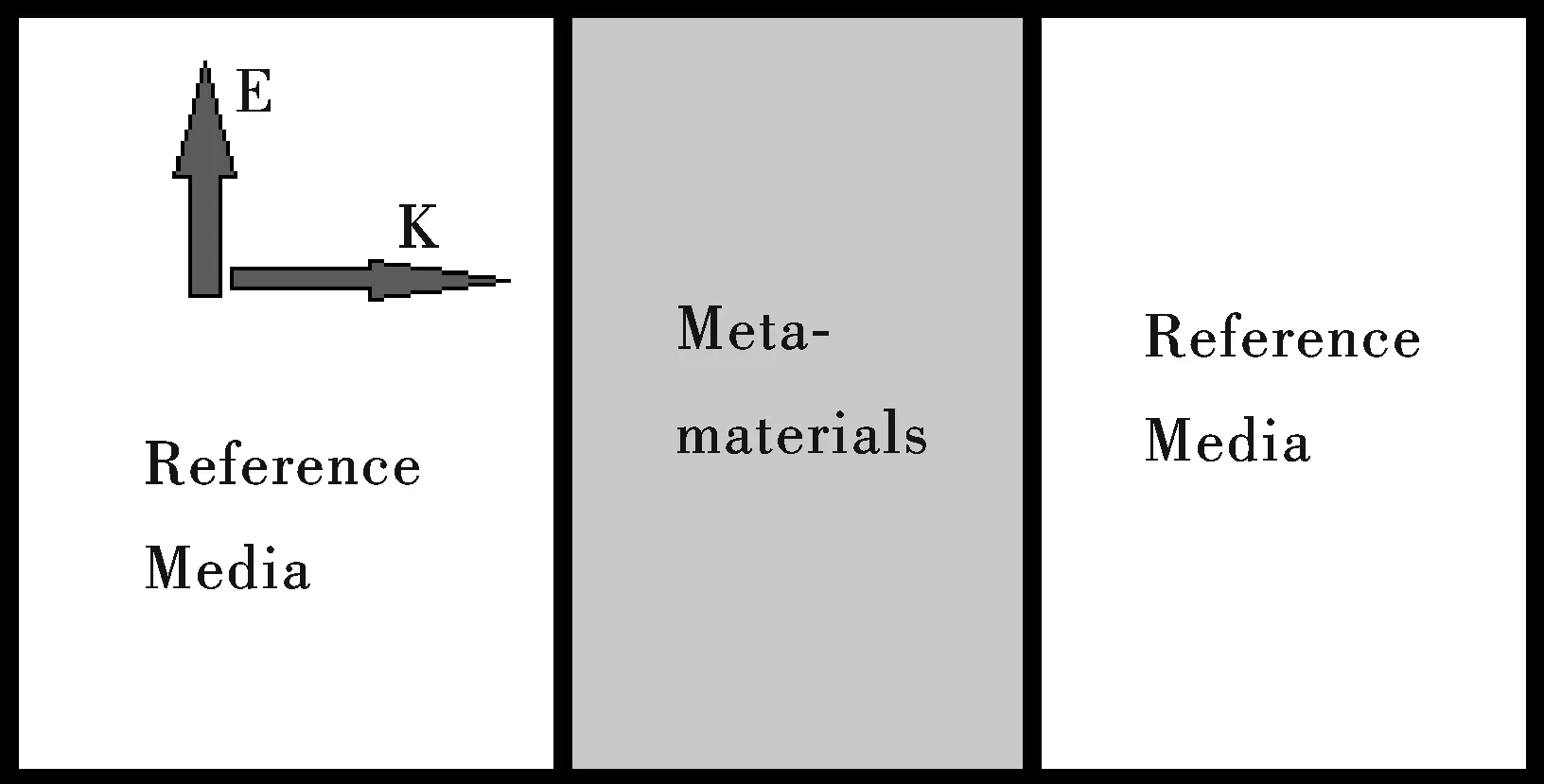
图1 GCPA方法计算特异材料有效媒质性质的原理图

如图1，将电磁特异材料放入背景材料中，当计算特异材料有效媒质的时候，我们通常考虑周期性的特异材料结构，这样不仅利于计算，而且利于实验上制备样品．考虑电磁波在特异材料结构中的散射问题，为了使问题简化，我们选取一层特异材料进行研究而把其他区域替换成背景媒质，其介电常数和磁导率分别用εref和μref来表示，而且它们可以被任意的调控．我们选取的这一层有效媒质足够厚，它的性质可以代表特异材料整体的性质．在这种简化下，电磁波的传播可以通过格林函数 (Green Function)方法进行求解[13]．

考虑电磁波垂直入射到特异材料层的情况，并且确定入射波的极化，这种情况下我们的问题可以简化为一维标量方程的求解，定义一个格林函数

(1)

(2)

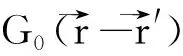
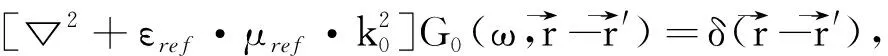
(3)

G=G0+G0VG=G0+G0TG0，

(4)

其中的T=V+G0VG0+G0VG0VG0+…=V(1-G0V)-1是标准的T矩阵．

若对散射体系进行均匀化，我们需要对散射体系做构型平均[13]，做过构型平均的格林函数可写为：

〈G〉c=G0+G0〈T〉cG0.

(5)

定义函数

(6)

利用(6)并运用傅立叶变换将格林函数写为：

(7)

我们发现公式(7)中∑正是电磁波传播过程中电磁波模的自能(Self-Energy)，这和研究电子结构中的自能项非常类似[14]．(7) 式说明了电磁波在特异材料体系中传播时，它仍然可以视作一个自由的模式，只是多了自能修正项．

根据散射理论[13]，在弱散射极限下，自能可以写成：

∑(ω,k)≈T(k,k)/L.

(8)

它和体系沿入射方向的散射振幅有关，这里的L是体系的尺寸因子，起归一化的作用．下面来求解T矩阵，由于电场满足(1)式，我们可以利用格林函数和T矩阵进行求解：

(9)

其中|φ0〉=exp(ikrefr-ωt)是在背景媒质中的自由波函数．这里省略了时间因子e-iωt．假设已经求解出体系的S参量，那么利用极限讨论可以得到如下结果:

φ(z)=S21eikrefz,z→∞,φ(z)=eikrefz+S11e-ikrefz,z→-∞.

(10)

利用(9)和(10)式可以得到

T(kref,kref)=2krefi(S21-1),T(-kref,kref)=2krefiS11.

(11)

由此不难发现，自能∑可以通过计算S参量得到．

接下来讨论如何确定特异材料的有效介电参量，方法是利用GCPA的思想，通过改变背景媒质的介电常数εref和磁导率μref使得体系的自能为零.此时特异材料的有效介电参量就和背景媒质的介电参量相同，从而得到体系的有效媒质．但是GCPA的思想在大多数情况下并不适应，因为体系的散射损耗总是存在的，特别是当电磁波的频率接近体系的共振频率时，系统的散射损耗更大，因此很难使得体系的自能为零．为了解决这个问题，我们将GCPA的方法进行扩展，通过定义电磁波态密度函数DOS来确定体系的有效媒质参量，其定义为:

(12)

态密度函数DOS不同于传统的概念，其物理意义是：在频率为ω处波矢量为k的电磁波模式的存在概率．在特定频率下，能使得DOS最大化的波矢k决定该频率处电磁波的模式．在一个纯净的系统中，体系的自能为零，体系的态密度DOS是一个Delta函数，体系中的电磁波模式是一个纯净完美的模式；但是在一个散射系统中，体系的态密度DOS不再是一个Delta函数，体系中的电磁波模式也不再是一个纯净完美的模式，而是一个“准模”(Quasi Mode)．

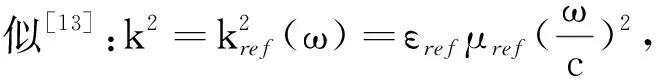
因此可将态密度写成如下形式：

(13)

其中的自能项∑eff是背景材料的介电常数εref和磁导率μref的函数．在这个近似下，态密度函数只依赖于εref，μref，因此只需要调节这2个量使得DOS最大，体系的有效介电常数εeff和磁导率μeff就等于背景材料的介电常数εref和磁导率μref．

2 理论的数值模拟

在这一部分，我们通过一维AB结构的特异材料体系来验证“准模”理论．其结构如图2所示，包围特异材料的背景媒质的介电常数εref和磁导率μref可以任意调节．为了方便起见，只计算一个单元的特异材料，在x，y方向使用周期性边界条件，因此体系在x，y方向等效为特异材料的周期性阵列，单元在x，y，z方向的晶格常数为16 mm×6 mm×7.5 mm．电磁波沿z方向传播，电场沿x方向，磁场沿y方向．对于一维AB结构，如图2(b)所示，这里的A,B代表2层均匀的介质，设定它们的介电及几何参量为εA=16，μA=1，dA=3.75 mm；εB=4，μB=1，dB=3.75 mm．

(a)准模方法计算特异材料有效媒质参量的装置图 (b) 一维AB结构图2

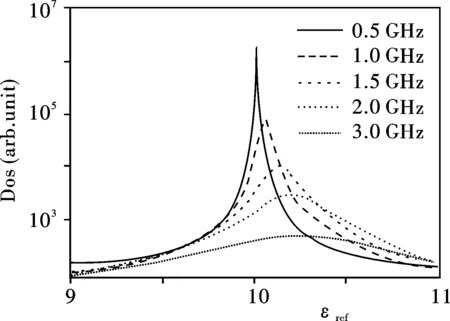
图3 一维AB结构体系的态密度DOS随背景材料的介电常数εref的关系曲线，计算的频率包括f=0.5,1.0,1.5,2.0,3.0 GHz，背景材料的磁导率μref恒为1

要研究体系的有效媒质性质，利用第一部分介绍的准模方法，我们不断变换背景材料的介电常数εref和磁导率μref并计算体系的S参量，以此来计算体系的自能和态密度DOS．由于这个体系不存在磁相应，因此我们设定背景材料的磁导率μref恒为1，只来改变背景材料的介电常数εref，通过一系列的计算，我们得到图3中的f=0.5,1.0,1.5,2.0,3.0 GHz几个频率处，体系的态密度DOS与背景材料的介电常数εref之间的关系图线．

参考文献：

[1] PENDRY J B. Negative refraction[J]. Contemp Phys, 2004, 45:191-196.

[2] PENDRY J B, HOLDEN A J, STEWART W J,etal. Extremely low frequency plasmons in metallic mesostructures[J]. Phys Rev Lett, 1996, 76:4 773-4 778.

[3] PENDRY J B, HOLDEN A J, BOBBINS D J,etal. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Trans Microwave Theory Tech, 1999, 47:2 075-2 082.

[4] POPA B, CUMMER S A. Detenmining the effective electromagnetic prop-erties of negative-refractive-index metamaterials from internal fields[J]. Phys Rev B, 2005, 72:165102.

[5] BAENA J D, BONACHE J, MARTIN F,etal. Equivalent circuit models for split ring resonators and complementary split rings resonators coupled to planar transmission lines[J]. IEEE Trans Microw Theory Tech, 2005, 53:1 451-1 456.

[6] LIU R P, ZHAO B, LIN X Q,etal. Evanescent-wave amplification studied using a bilayer periodic circuit structure and its effective medium mode[J]. Phys Rev B, 2007, 75:125118.

[7] AZNAR F, BONACHE J, MARTIN F,etal. Improved circuit model for left-handedlines loaded with split ring resonators[J]. Appl Phys Lett, 2008, 92:043512.

[8] BAKER-JARVIS J, VANZURA E J, KISSICK W A. Improved technique for detennining compley peanittivity with the transmission /reflection method[J]. Trans IEEE Microw Theory Tech, 1990, 38:1 096-1 099.

[9] SMITH D R, SCLMLTZ S, MARKOS P,etal. Determination of effective permittivity and permeability of metamaterials from reflection and trans-mission coefficients[J]. Phys Rev B, 2002, 65:195104.

[10] LI J, ZHOU L, CHAN C T,etal. Photonic band gap from a stack of positive and negative index materials[J]. Phys Rev Lett, 2003, 90:083901.

[11] ROCKSTUHL C, PAUL T, LEDERER F,etal. Transition from thin-film to bulk properties of metamaterials[J]. Phys Rev B, 2008, 77:035126.

[12] ZHOU J, KOSCLMY T, KAFESAKI M,etal. Size dependence and convergence of the retrieval parameters of metamaterials[J]. Photon Nanostr Fundam Appl, 2008, 6:96-100.

[13] SHENG P. Introduction to wave scattering, localization, and mesoscopic phenomena[M]. San Diego:Academic Press, 1995.

[14] ZIMAN J M. Principles of the theory of solids[M]. 2 ed. London:Cambridge University Press, 1972.