关于信号滤波中的频率逼近

黄 霞

(杭州电子科技大学理学院数学研究所,浙江杭州310018)

0 引 言

频率分析问题研究的是通过一组已知的离散时间信号值{x(m)}∞-∞定出未知的频率的近似值[1-6]。近几年,一些学者继续研究此类问题,插入一个正的权因子cm[7](满足一定条件),对ΨN(θ)的定义作了进一步的推广。本文给出测度的一种新的定义形式,研究此测度的弱*收敛性,从而由与之相关的Szegö多项式序列的零点的性质得出原有频率的近似估计等问题。

1 信号测度的弱*收敛性

定义1

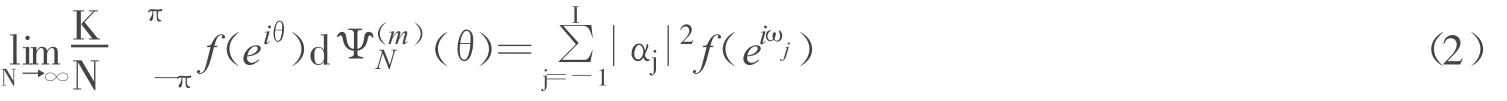
为此,选择ε＞0,使得当j≠s时,ωj∉[ωs-ε,ωs+ε]。dθ,在式 2中考虑 j=k=s一项,有(ei(ωs),,对于其他项:j≠s,k≠s时误差为),j=s或k=s时误差为)。因此

从式2可得出对充分大的N:

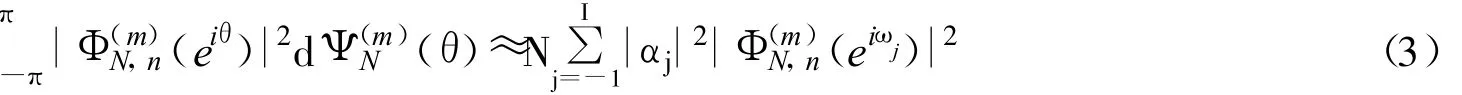
证明 由定义:

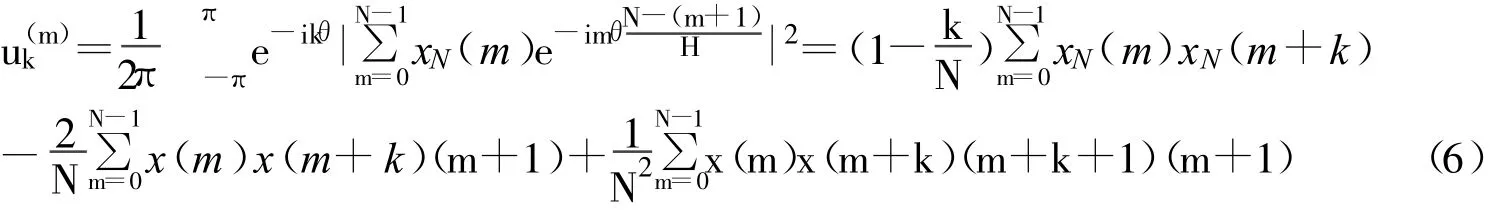
利用阿贝耳变换:

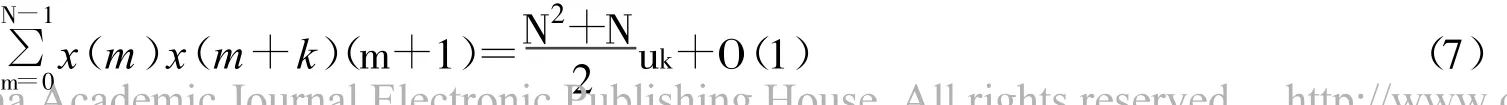
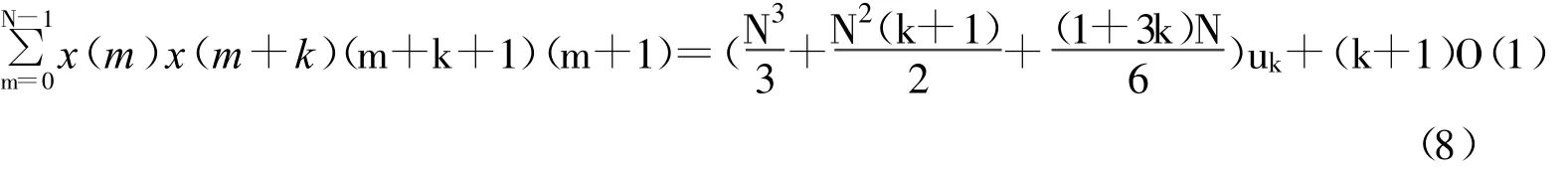
将式7和8代入式6中处理可得结论。

2 Szegö多项式的零点逼近信号频率

依据分布矩量作出Szegö多项式序列。

关于分布dΨ(θ)的首项系数为一的正交多项式可以写成:

Φn(z)=,n=1,2,…,2I+1。与此类似可定义关于dθ)的首项系数为一的正交多项式(z),就是 Φn(z)里用代替uk得到的多项式。

证明 由定义2和定理2可得对每个固定的n≥1,当N→∞时有

引理2 Q(≠0)表示零点位于|z|＜1的任一多项式,如果λ∈C,满足|λ|＜1,则多项式T(z)[8]有:

式9的零点位于|z|＜1上。其中Q*(z)=znQ(1/)称其为Q(z)的逆多项式。

证明 运用反证法

假设有一点z0,使得 T(z0)=0且|z0|≥1,由式 9,有|z0Q(z0)|=|λQ*(z0)|,|z0|=|λQ*(z0)/Q(z0)|≤|λ|＜1,与假设矛盾。

定理4 假设α0＞0,则对固定的n≥2I+1,当N→∞时,(z)的2I+1个零点(合适的顺序)的最大模接近点eiωj,-I≤j≤I。

式中,Qn-2I-1(z)是一个n-2I-1次的首项系数为一的多项式,其零点都位于圆盘|z|＜1上。

用数学归纳法证明:

n=2I+1的情况如定理3所述。假设n=t(＞2I+1)时结论是成立的,由已知(z)的逆多项式。不失一般性,考虑子序列当k→∞时(z)∈Pt,Pt表示t次多项式的集合。由式9可得 R(z)=z S(z)+δt+1S*(z)。由归纳假设 S(z)=Q(z)Φ2I+1(z),Q(z)是 t-2I-1次首项系数为1的多项式,则式9可写成 R(z)=zΦ2I+1(z)Q(z)+δt+11(z)Q*(z)=Φ2I+1(z)Q(z)+δt+1Φ*(z),这里利用Φ2I+1(z)=1(z),结合引理2得到了结论。

3 结束语

通过上述讨论可得:频率分析问题中的Szegö多项式的次数若严格小于临界点eiωj的个数,则不能解决问题。换言之,多项式的次数须大于(或等于)临界点的个数方可。

[1] JonesWB,Njåstad O,Saff E B.Szegöpolynomials associated with Wiener-Levinson filter[J].ComputApp lMath,1990,32(3):387-406.

[2] JonesWB,Njåstad O,Thron WJ,et al.Szegöpolynomials applied frequency analysis[J].Comput App lMath,1993,46(1-2):217-228.

[3] Li X.Asymptotics of columns in the tab le of orthogonal polynomials with varying measures[J].Methods Appl Anal,1995,2(2):222-236.

[4] JonesWB,SriRanga A.Lecture notes in Pure and App lied Mathematics[M].New York:CRC Press,1998:399-408.

[5] Njåstad O,Waadel H.Asymptotic properties of zeros of orthogonal rational functions[J].Comput ApplMath,1997,77(1-2):255-275.

[6] Njåstad O,Waadel H.Generalized Szegötheory in frequency analysis[J].Math Appl,1997,(1):280-307.

[7] Petersen V.Weak convergence and boundedness properties of measures in frequency analysis[J].Math AnalApp l,2000,(1):87-104.

[8] Pan K,Saff E B.Asymptotics for zeros of Szegöpolynomials associated with trigonometric polynomial signals[J].Appr Th,1992,71(3):239-251.