尾气余热多孔介质热电材料发电的数值试验

李 博,徐江荣

(杭州电子科技大学理学院,浙江杭州310018)

0 引 言

汽车行驶过程中,汽油机的发动机输出动力占燃油总热量的不到30%,其余热量都通过引擎冷却水和尾气排出车外[1]。其中排气管中的废气,温度一般在500℃左右,高负荷工作状态下可以达到750℃[2]。若可以对这些高温尾气进行再利用,那么不仅节约了能源,而且减少一定程度的大气污染。汽车尾气发电有两种形式:一种是基于朗肯循环的低沸点工质发电;另一种是基于塞贝克效应的温差发电[3]。塞贝克效应是温差发电的理论依据,当一根金属导线两端存在温度差时,金属导线两端会形成电势差。关于温差发电,美国和日本的研究成果最为丰富,美国能源部和日本通产省的研究人员一致认为,在近期温差发电能量转换系统的效率将有望达到15%,而且温差发电技术在经济上也是可行的[1]。日本东京技术学会的碳循环与能源研究中心,在利用多孔介质热电材料进行超绝热燃烧发电这一领域研究成果比较多,设计一个将燃烧热转化为电能的系统,基于多孔介质热电材料中的往复流动超焓燃烧[4]。低热值的废气在多孔介质催化剂中燃烧,催化剂两端是热电材料多孔介质,燃烧过程中催化剂两端可以形成温差。经计算,全部的燃烧热转换为电能的比率,已经接近热电装置本身的转化效率。本文讨论的是温差发电,提高排气管内的温度梯度是本文考虑的重点。

1 数值模拟

经过多次数值试验,取数值实验效果较好的结果,确定模拟排气管如图1所示,模拟排气管为自主设计。进口一为尾气的入口,其温度较高,进口二为大气气流的入口,其温度较低。利用两个进口的不同温度使多孔介质内部产生较大的温度梯度,另外在1长的排气管中填充多孔介质热电材料,利用多孔介质比表面积大,超焓温度等特性,提高温度梯度进行热电转化,从而提高汽车尾气余热发电的效率。

数值模拟区域从两个进口开始,到出口结束,x取值-0.05到1.1,单位m。y方向与z方向的最小值都为-0.1m,最大值都为0.1m。进气管、排气管均为长度0.05m、直径0.05m的圆筒状,填充多孔介质的区域为直径0.2m、长1m的圆柱体。气体与固体的热物性参数均取自文献4、5。

多孔介质为蜂窝状,其形状规则,每平方厘米大约有15.5个正方形的小孔[4],孔中间插有U型热电材料β-FeSi2。研究中做如下假设:(1)排气管的管壁是绝热的;(2)由于蜂窝状多孔介质具有规则的结构,所以可以看做是一个连续的固体,而多孔介质的热物理性质是在通过排气管的气体热物理性质的基础上,所以可以使用孔隙率作为修正系数;(3)由于多孔介质的特性,将蜂窝状多孔介质的孔隙率设为0.8[6],此时多孔介质具有大的比表面积,导热系数和热容量都比气体大得多;(4)忽略辐射换热的影响,忽略尾气与蜂窝状多孔介质前后端面的对流换热。因此多孔介质传热的数学模型表述如下:

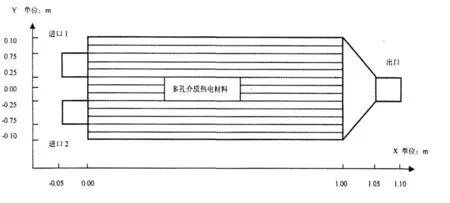
图1 多孔介质热电材料系统示意图及坐标

其中,Si是由多孔介质引起的阻力项,由Ergun公式计算[7],α为渗透性,keff为多孔介质的有效热传导系数,下标g为气相,下标s为固相,μt为湍流脉动速度,Gk为层流速度产生的湍流动能,Gb为浮力产生的湍流动能,Prt是湍流能量的普朗特数,为0.85,gi是重力在i方向上的分量,β是热膨胀系数,分别表示为

参数C1ε,C2ε,C3ε和Cμ为常量,σk和σε分别为k方程和ε方程的湍流Prandtl数,由经验系数给出[5]。其中C3ε=tan|v/u|,这里v是平行于重力方向的速度分量,u是垂直于重力的速度分量。T为温度,p为静压,t为时间,v为速度,η为孔隙率,xi(i=1,2,3)为流向坐标,λ为热导率,ρ为密度,h为焓,kg,ks分别为气体和固体内部的热传导系数,下标in为气流的入口。

求解的结果为稳态的,因此方程中可以省去关于时间的部分。计算区域是长度为1m、直径0.2m的圆筒状多孔介质区域,以及两个进口一个出口的区域。进口一的温度T1=723K,进口二的温度T2=293K,两个进口的速度相同,均为v=vin。出口∂T/∂xi=0。

2 结果和讨论

根据轿车的排气量,本文采用了速度为0.8m/s和10m/s两个速度进行数值模拟,分别模拟轿车怠速与高速行驶时的情况。进气速度为10m/s,z=0时截面的速度场如图2所示。根据模拟结果可知,速度为0.8m/s时,在x=0.2m时,管内气体速度基本达到稳定状态;速度为10m/s时,在x=0.6m时,管内气体速度基本达到稳定状态。速度在10m/s的湍动能分布如图3所示。从模拟结果可知,速度为0.8m/s时,湍动能主要集中在x＜0.3m之前;速度为10m/s时,湍动能主要集中在x＜0.5m之前。而湍动能集中的地方,正是对流换热的集中区域,因此这个区域也是温差发电器安装的地方。由于温差发电的效率与温度梯度息息相关,所以温度场的模拟也是各项数值模拟中最为重要的,速度在0.8m/s与10m/s时的等温线分布如图4所示。

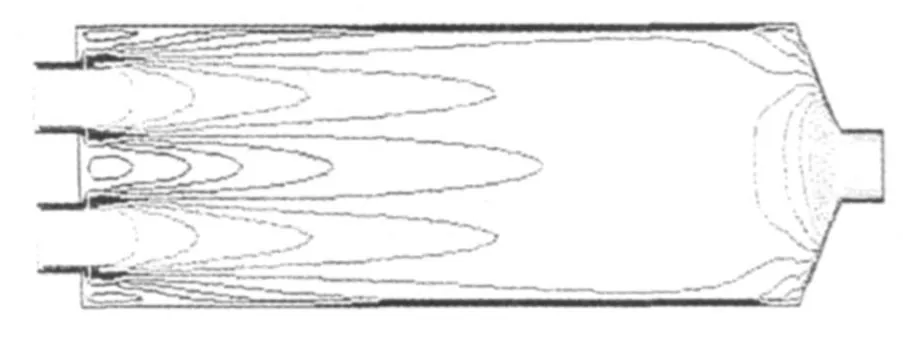
图2 进气速度10m/s时的速度场

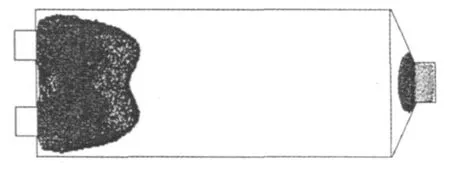
图3 进气速度10m/s时的湍动能

图4 温度场

速度为0.8m/s时,x=0～0.5m时温度梯度较大;当速度为10m/s时,x=0～0.7时温度梯度较大。对这两种不同速度的情况取z=0,x为0.1、0.3、0.5,温度沿截面直径y=-0.1～0.1的变化情况如图5、6所示。进气口进气速度的大小对湍动能的影响是非常明显的。速度较大时,尾气流量随之较大,这时湍动能也相应较大,气固之间的对流换热明显加强,温度场也就具有较大的温度梯度,并且温度变化明显的区域在排气管的前半部,即x=0～0.5的区域。而随着进气速度的增大,具有较大温度梯度的区域随之向后移动,速度为10m/s时,温度变化明显的区域在x=0～0.7。

3 结 论

通过数值模拟得知,排气管内沿X方向,气体流速还未稳定的时候,湍动能比较大,这时的对流换热比较明显,沿Y方向的温度梯度比较大。因此安装U型热电材料时,考虑到温度场、温度梯度的情况,应该按Y方向竖直放置,这样U型热电材料的两端电动势才能随着温差的增大而加大。

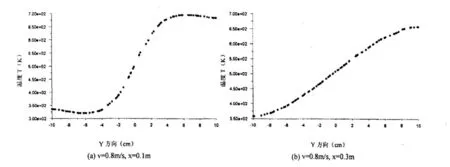
图5 温度沿y轴的分布

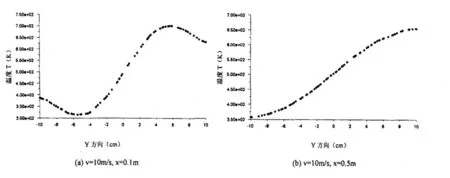
图6 温度沿y轴的分布

[1] 董桂田.汽车发动机排气废热的温差发电[J].北京节能,1997,15(4):7-9.

[2] 蔡锐彬,杨建威,陈子健.汽车排气热反应净化机理的研究[J].机械工程学报,1997,10(4):65-69.

[3] 何元金,陈宏.温差发电——一种新型绿色的能源技术[J].工程物理,2000,10(2):36-41.

[4] KatsunoriHanamura,Tomoyuki Kumano,Yuya Iida.Electric poeer generation by super-adiabatic combustion in thermoelectric porous element[J].Energy,2005,30(2):347-357.

[5] 周光垌,严宗毅,许世雄,等.流体力学[M].北京:高等教育出版社,2000:353-363.

[6] 杜礼明,解茂昭.预混合燃烧系统中多孔介质作用数值研究[J].大连理工大学学报,2004,44(1):70-75.

[7] Ergun S.Fluid Flow through Packed Columns[J].Chem Eng Prog,1952,48(2):89-94.