机器带中断的误工问题的近似排序算法
叶春花,沈 灏
(杭州电子科技大学理学院,浙江杭州310018)
0 引 言
本文研究生产计划制定后机器突发故障时的应急排序问题。文献1提出了考虑工件移机运输时间的机器带故障的两台平行机排序问题。文献2考虑了机器中断,但没有考虑不确定因素。文献3提出了P2|D=∞,T≠0|∑U′ij问题的一个差界算法。文献4提出了单台机误工工件数最小化问题的算法,这个算法称为Moore-Hodgson算法。文献5给出Moore-Hodgson算法最优性的证明。本文考虑一般的中断时间D,分别讨论T=0和T≠0情况下的排序问题P2|D,T|∑U′ij。
1 问题介绍
考察如下排序问题:设有两台平行机M1,M2。Jij为中断前计划在机器Mi上加工的第j个工件,Jij的加工时间为Pij。其中一台机器在不可知情况下中断,假设中断开始时间为t1,终止时间为t2,持续时间为D=t2-t1。设Cij表示原计划中 Jij的完工时间,表示重新排序后 Jij的完工时间,令 U′ij=决策者在t=t1重新排序,目标使∑U′ij为最小。不失一般性,假设M 1中断 ,M 1工件可以转移到M2加工 ,M1恢复后 ,M2工件也可以转移到M1加工 ,转移时间为T,分两种情况讨论:问题1,P2|D,T=0|∑U′ij;问题2,P2|D,T≠0|∑U′ij。
2 算法及定理
2.1 问题1 P2|D=∞,T=0|的算法
设t1时刻,M1,M 2上正在加工的工件为J1s,J2e。t2时刻,M1,M2上正在加工的工件为J1t,J2f。若C1t≤C2f,如图 1所示,若 C1t>C2f,如图2所示。
步骤1 若C1t>C2f,那么在工件J2f后依次选取h个M2工件使得将前h-1个工件转移到M1上从t2时刻开始按M2上的先后序加工。若C2e-t1≥P1s,则转步骤2,否则转步骤3;
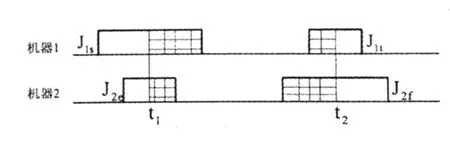
图1 C1t≤C2f的示意图
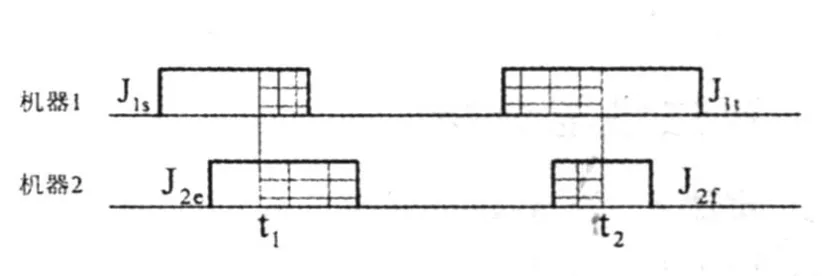
图 2 C1t>C2f的示意图
步骤2 工件集{J1s,J1,s+1,…,J1t,J2e,J2,e+1,…,J2f}在t1时刻开始在机器M2上按单台机最优算法Moore-Hodgson算法排序,误工工件按任意顺序在J1n1或J2n2后加工;
步骤3 工件集{J1s,J1,s+1,…,J1t,J2,e+1,…,J2f}在C2e时刻开始在机器M2上按单台机最优算法Moore-Hodgson算法排序,误工工件按任意顺序在J1n1或J2n2后加工。
2.2 问题2 P2|D,T≠0|的算法
引理 若π*中在 r时刻之前开工的工件都是M2工件,则π*为P2|D,T≠0|的最优排序。
定义2 称π*中r时刻正在机器M 2上加工且尚未完工的工件为跨越工件,记跨越工件在r时刻之后加工的时间长度为T1,记在时刻之前开工的工件集为A1,在r时刻或之后开工的工件集为A2。
设r=t1+T,由于考虑运输时间,原来M1上r时刻前开工的工件没转移就已误工,称为哑工件,如图3所示。对于图2,M2工件转移到M1加工至少有一个工件误工,而考虑M2工件转移到M1加工,至多可以减少J1t这个工件的误工可能性,所以,图2不需要考虑M2工件转移到M1加工的情况。
设π*中在r时刻前开工的M1工件为{J1j1,…,J1jk},令。算法2考虑r时刻之前加工的M 1工件与r时刻之后加工的M2工件交换,使增加的误工工件数尽量少,如图4所示。
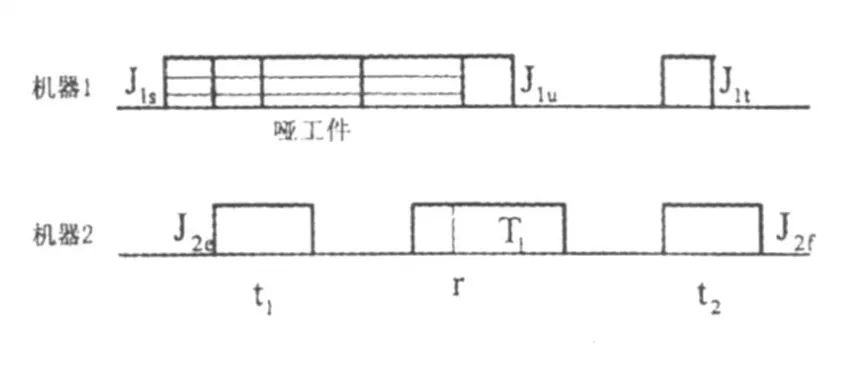
图3 T>0时工作示意图

图4 π*排序与近似排序的比较
算法2 (P2|D,T≠0|∑U′ij的近似算法):
步骤1 计算问题1去掉哑工件后的最优算法排序,将工件集{J1u,…,J1t,J2e,…,J2f}执行算法1步骤2,将工件集{J1u,…,J1t,J2,e+1,…,J2f}执行算法1步骤3,选择值小的作为最优序π*;
步骤2 若π*在 r时刻之前不含M 1工件,则π*即为问题2的最优序,算法终止,否则转下一步;
步骤3 机器M2上依次选取π*中开工时间大于或等于r的y个M2工件{J2b1,…,J2by},使得≥P-T1,而P2bv<P-T1(当π*中不存在跨越工件时,令T1=0),令Q=
步骤4 若Q=P-T1,那么在M 2上先安排A1|{J1j1,…,J1 jk},然后安排{J2b1,…,J2by},接着在r时刻按照M1上的先后序加工π*中转移到机器M2上的在J2by之前加工的M1工件,再按π*中的先后序加工剩余的其他工件,最后以任意顺序在J1n1或J2n2之后加工哑工件;若Q>P-T1,那么在M2上先安排A1|{J1j1,…,J1jk},然后安排{J2b1,…,J2by-1},接着在r时刻按照M1上的先后序加工π*中转移到M2上的在J2by之前加工的M1工件。若J2by不误工,则加工J2by。否则放在所有工件后加工,再按π*中的先后序加工剩余的其他工件,最后以任意顺序在J1n1或J2n2之后加工哑工件。
3 算法性能分析
定理1 设A(I)是算法2关于问题2的任意实例的目标值,OPT(I)是最优算法关于实例I的目标值,则|A(I)-OPT(I)|≤1。
证明 分3种情形证明:
情形1 π*不含跨越工件。若Q=P,误工工件个数不改变。若Q>P,{J2b1,…,J2by-1}提前完工,交换后{J1j1,…,J1jk}不误工,产生Q-P个单位的空闲。若 P2by≤Q-P,则 J2by不误工,误工工件个数不改变。否则J2by误工,新增一个误工工件;
情形2 π*有一个跨越工件为M1工件。若Q=P-T1,{J2b1,…,J2by}提前完工,交换后加工{J1j1,…,J1 jk}时间为T1+Q=P,误工工件个数不改变。若Q>P-T1,{J2b1,…,J2by-1}提前完工,交换后加工{J1 j1,…,J1jk}时间为T1+Q>P,不误工,此时产生T1+Q-P个单位空闲。若P2by≤T1+Q-P,J2by不误工,误工工件个数不改变。否则J2by误工,新增一个误工工件;
情形3 π*有一个跨越工件为M2工件。若Q=P-T1,{J2b1,…,J2by},提前完工,机器在时刻r前有P-Q=T1个单位空闲,将跨越工件提前加工,不误工。交换后加工{J1j1,…,J1jk}时间为T1+Q=P,误工工件个数没有改变。若Q>P-T1,{J2b1,…,J2by-1}提前完工,机器在r时刻前有P-(Q-p2by)=P-P2bv>T1个单位空闲,将跨越工件提前加工,没有误工。交换后加工{J1j1,…,J1 jk}时间为T1+Q>P,此时产生T1+Q-P个单位空闲。若P2by≤T1+Q-P,J2by不误工,误工工件个数不改变。否则J2by误工,新增一个误工工件。
[1] Lee Chung-Yee,Joseph Y-T Leung,Yu Gang.Two machine scheduling under disruptions with transportation considerations[J].Journal of Scheduling,2006,(9):35-48.
[2] Qix,Band JF,YuG.Disruption management for machine scheduling,the case of SPT schedu les,internet[J].Production Economics,2006,103(1):166-184.
[3] 叶赛英,沈灏,魏小兰.机器带故障的两台机排序问题的一个近似算法[J].杭州电子科技大学学报,2008,28(2):90-92.
[4] Moore JM.Onemachine sequencing algorithm for minimizing the number of late jobs[J].Management Science,1968,(15):102-109.
[5] 孙叶平,唐万梅,唐国春.Moore-Hodgson算法最优性的证明[J].重庆师范大学学报,2007,24(3):4-7.

