采用Radon变换和二维主成分分析的步态识别算法

王科俊，贲晛烨，2，刘丽丽，3

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001;2.哈尔滨工业大学交通科学与工程学院，黑龙江哈尔滨150090;3.中国科学院沈阳计算技术研究所有限公司，辽宁沈阳110171)

步态识别是根据人们走路姿势的不同来识别其身份的.由于个体的身形和运动行为的特征不同，为通过人的行走方式来识别身份提供了线索.步态识别相对于其他生物特征识别具有非侵犯性、非接触性、对系统分辨率要求不高、可适应远距离、难以伪装、受环境影响小等优点.步态识别在安全监控、人机交互、医疗诊断等领域具有广泛的应用前景和经济价值［1］.因此，步态是远距离身份识别的最佳首选之一.

自从“911”事件以后，世界各国加强对身份认证的重视，很多高校和研究机构也展开了远距离下的人的检测、分类与识别，例如马里兰大学、麻省理工学院、卡内基梅隆大学等.国内最早是中科院自动化所的王亮等［2］提出了一种人体轮廓解卷提取距离信号的步态识别算法.其后，西安电子科技大学、西安交大、复旦大学、上海交大、南京理工大学、华中科技大学和哈尔滨工程大学等诸多高校都开展了步态识别的研究工作.目前步态识别方法可以分成3类:二维步态识别、三维步态识别以及两者相结合的方法.二维步态识别就是在单摄像机拍摄的视频中通过轮廓提取最低层的信息进行分析识别;而三维步态识别方法［3］则通过多个摄像机对人体三维模型跟踪，三维重建人体结构，分析关节运动位移来识别身份.另外很多研究者着手用Radon变换提取步态特征.黄凤岗等人［4］对下肢进行Radon变换，提取运动角度信息，对所得到的特征使用经典主成分分析(principal component analysis，PCA)后进行动态时间规整，该方法计算复杂，处理速度慢，不适合实时的步态识别，而且该算法仅仅是在较小的数据库上做的尝试.Boulgouris等人［5］也尝试了Radon变换结合线性判别分析(linear discriminant analysis，LDA)提取步态特征.笔者前期也做过Radon变换结合经典 PCA提取步态特征的方法［6］，但是由于LDA、PCA总是首先要把二维图像矩阵转换成一维向量，造成相关矩阵的维数较高，特征值、特征向量的获取很耗时，而且在文献［6］也没有对模板构造的实质进行分析.本文在文献［6］基础上改用2DPCA［7］的方法直接对矩阵降维.首先对一个步态周期内的每一幅图像进行Radon变换，再通过模板构造提取步态特征矩阵，并对模板构造的实质进行阐述，最后通过实验确定较好的Radon变换参数和模板构造的频率参数，得到了Radon变换方法结合列2DPCA提取步态特征是比较有效的结论.

1 步态序列图像预处理

为了提取人体目标，首先从原始视频中提取单帧图像进行灰度变换(如图1(a));然后逐帧计算各像素点的中值，作为整个序列的背景图像(如图1(b));最后，采用背景减除法提取人体目标(如图1(c))，用数学形态学填补二值化图像的空洞、单连通分析提取人的侧影(如图1(d)).为了消除图像大小对识别的影响应使人体居中，将图像的大小统一为64 ×64(如图 1(e))［8］.

图1 图像预处理Fig.1 Image preprocessing

2 步态特征提取

运动人体轮廓的宽高比成周期性变化，因此在提取步态特征只需在一个周期中进行.为了同时刻画人身体形状的静态特征和运动的动态特征，采用Radon变换的方法来提取步态特征，2DPCA算法直接对所得到的特征矩阵进行降维处理.

2.1 步态图像的Radon变换

设函数f(x，y)∈L2(D)在平面D区域平方可积，则 f(x，y)的 Radon 变换 Rf(ρ，θ)可表示如下:

式中:ρ是点(x，y)的极径，θ是点(x，y)的极角，有序实数对(ρ，θ)是点(x，y)的极坐标.

Radon变换的作用就是计算指定方向上图像的投影，对于二元函数f(x，y)则计算该函数在某一方向的线积分.如图2为步态图像的Radon变换结果.Radon变换后图像的第1列像素，对应于原始图像在垂直方向的投影;变换后图像的正中间的一列像素，对应于原始图像在水平方向的投影.很明显，水平方向的投影比垂直方向的投影范围大，这是因为人体固有的身形所致.采用Radon变换的方法提取步态特征的优点在于对前期处理中轮廓边缘的噪声点有较强的鲁棒性［6］.

图2 步态图像的Radon变换Fig.2 Radon transform of gait image

2.2 步态周期特征模板

周期序列图像的特征模板可定义为［9］

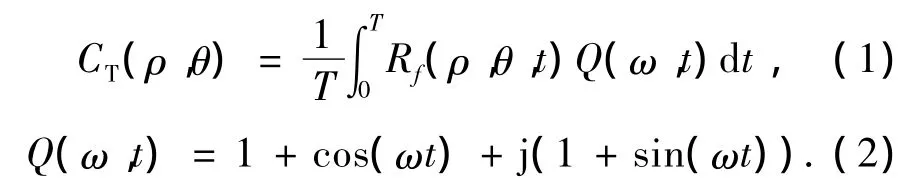
式中:Rf(ρ，θ，t)是Radon变换在时间上的线性插值，Q(ω，t)为加权函数，t为时间.在模板构造过程中，为了同时刻画人体运动中的身体结构特征和动态运动特征，必须选择加权函数Q(ω，t)中合适的频率值ω，将周期序列特征映射到一个特征矩阵中.时不变因子1+j是人体静态结构特征的权值，时变因子cos wt+jsin wt是步态运动参数的权值.

2.3 二维主成分分析(2DPCA)

由于Radon变换得到的步态特征维数较高，如果采用经典的PCA算法，即使采用奇异值分解的方法来求相关矩阵的特征值、特征向量，计算的数据量也依然很大，而2DPCA［10］直接对矩阵进行计算，计算量相对少很多.

考虑一个大小为m×n的图像X，Y就是相对应的X到方向为w的空间上的投影.

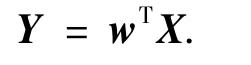
实际上，w的绝对值是无关紧要的，它仅仅是使Y乘上一个比例因子，重要的是选择w的方向.w方向的不同，将使样本投影后的可分离程度不同，从而直接影响识别效果.因此，问题转化为寻找最好的变换向量w*的问题，应使所有的样本投影到w*后，投影样本的总体散布矩阵最大.投影样本的总体散布矩阵可以用投影特征向量的协方差矩阵的迹来描述.从这种观点来看，可以采用下面的准则:

式中:SY表示训练样本的投影后特征矩阵的协方差，tr SY表示SY的迹.协方差矩阵SY表示如下:

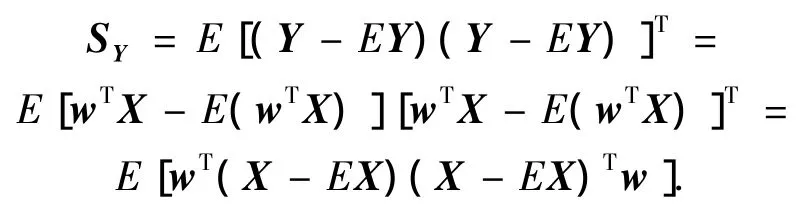
由矩阵的迹是一个数的性质，有

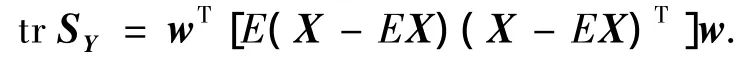
其中，

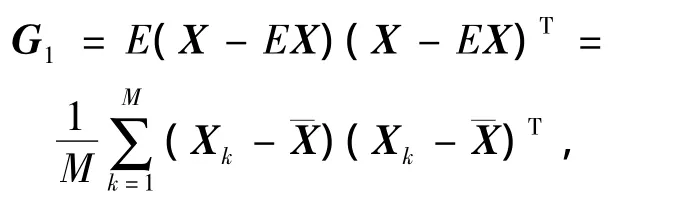
Xk(k=1，2，…，M)为第 k幅图像矩阵，M 为图像总数，均值图像为

因此，式(3)中准则可表示成:

式中:w是一个列向量.最大化该准则的向量w称为最优投影轴.直观上讲，这就意味着投影样本的总体散布矩阵在图像矩阵集合均投影到w上后被最大化了.

最优投影轴w*是最大化J(w)的列向量，也就是对应于G1的最大特征值的特征向量.一般情况下，只有一个最优投影轴是远远不够的，通常需要选择一组投影轴 w1，w2，…，wd，当然，这组投影轴要满足相互正交的约束条件，同时也要最大化准则J(w)，也即

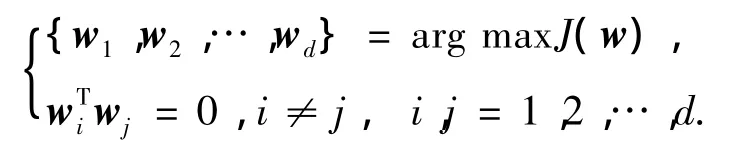
实际上，最优投影向量 w1，w2，…，wd是 G1的前 d个最大特征值所对应的相互正交的特征向量.

进一步分析得

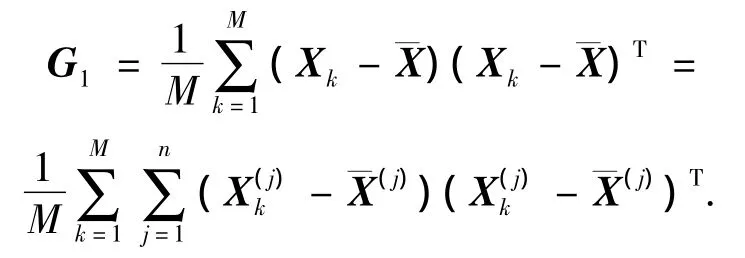
记

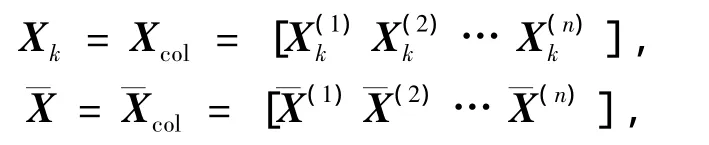
则w是根据图像列方向计算得到的投影矩阵.所以称Y=wTX形式为列2DPCA.

同理，可以得到另外一种行2DPCA形式:

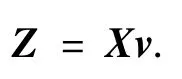
此时，协方差矩阵定义为

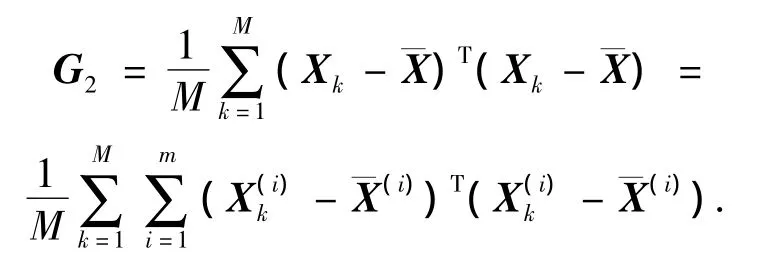
记

则v是根据图像行方向上计算得到的投影矩阵.

因此，2DPCA分成行、列2个方向.现在来讨论PCA与2DPCA的计算复杂度:考虑N个C类d维(d=m×n)的PCA与2DPCA算法的复杂度.两者计算均值的计算复杂度一致为O(Nd);PCA的相关矩阵的计算复杂度为O(Nd2)，2DPCA的行协方差的计算复杂度为O(Nn2m)，2DPCA的列协方差的计算复杂度为O(Nm2n);而计算它们的特征值、特征向量与矩阵的维数息息相关，PCA计算复杂度远远大于2DPCA;在投影时假设不进行特征向量的舍弃:PCA的计算复杂度为O(Nd2)，行2DPCA的计算复杂度为O(Nnd)，列2DPCA的计算复杂度为O(Nmd).综上所述，PCA整体的计算复杂度远远大于2DPCA.

3 步态的训练与识别

本文采用中科院自动化所提供的目标运动方向与摄像机光轴的方向成90°的CASIA步态数据库，图像库里总共124人.实验分为训练和识别2部分，每人前3个步态序列作为训练集，后3个序列作为测试集.在训练过程中，对一个步态周期内的单帧图像进行Radon变换，然后通过特征模板构造，提取整个步态周期的特征，再通过2DPCA进行最小均方误差意义下的最优数据压缩，训练得到2DPCA投影矩阵.在识别过程中，对待测试序列的一个步态周期内的单帧图像进行Radon变换，然后通过特征模板构造提取步态特征，根据训练好的2DPCA投影矩阵将所提取出来的特征从高维空间映射转换到低维空间，最后采用最近邻分类器将测试样本分到其所属类中.其中2DPCA计算特征矩阵Bi、Bj的欧式距离为

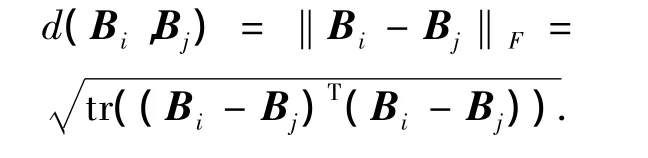
为了确定所提出方法的合理参数，做了3组实验:通过实验1研究行或列2DPCA算法对于Radon变换后提取的特征进行降维的有效性，通过实验2研究构造模板ω值的选取对识别性能的影响，通过实验3研究Radon变换中θ的选取对识别性能的影响.

3.1 行2DPCA与列2DPCA算法

根据文献［5］取 ω =π/2T.式(1)中，Radon变换中角度参数θ从0°～180°(180°除外)每隔3°取一次，此时经Radon变换提取的步态特征维数为60×95维.行2DPCA、列2DPCA方法的识别率与所降得的维数之间的关系如图3所示.由实验结果可以看出本文方法在这样的参数下，列2DPCA比行2DPCA有效，列2DPCA在列的维数降至为21时最好的识别率为0.795 7.

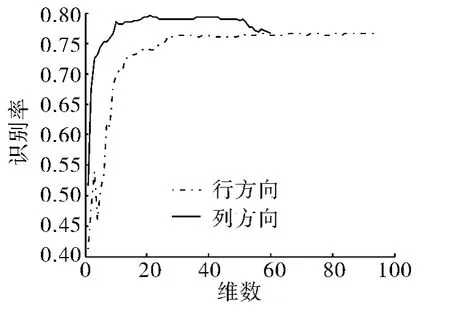
图3 行、列所降的维数与识别率的关系Fig.3 Relation between dimension reduced of rows ＆ columns and recognition accuracy

3.2 ω值的选取

Radon 变换中θ从0°～180°(180°除外)每隔3°取一次，定义压缩率为投影后得到的特征维数与原始特征的维数之比.在ω值分别为π/16T，2π/16T，…，16π/16T时，分别采用行2DPCA和列2DPCA方法进行实验.实验结果如表1所示.

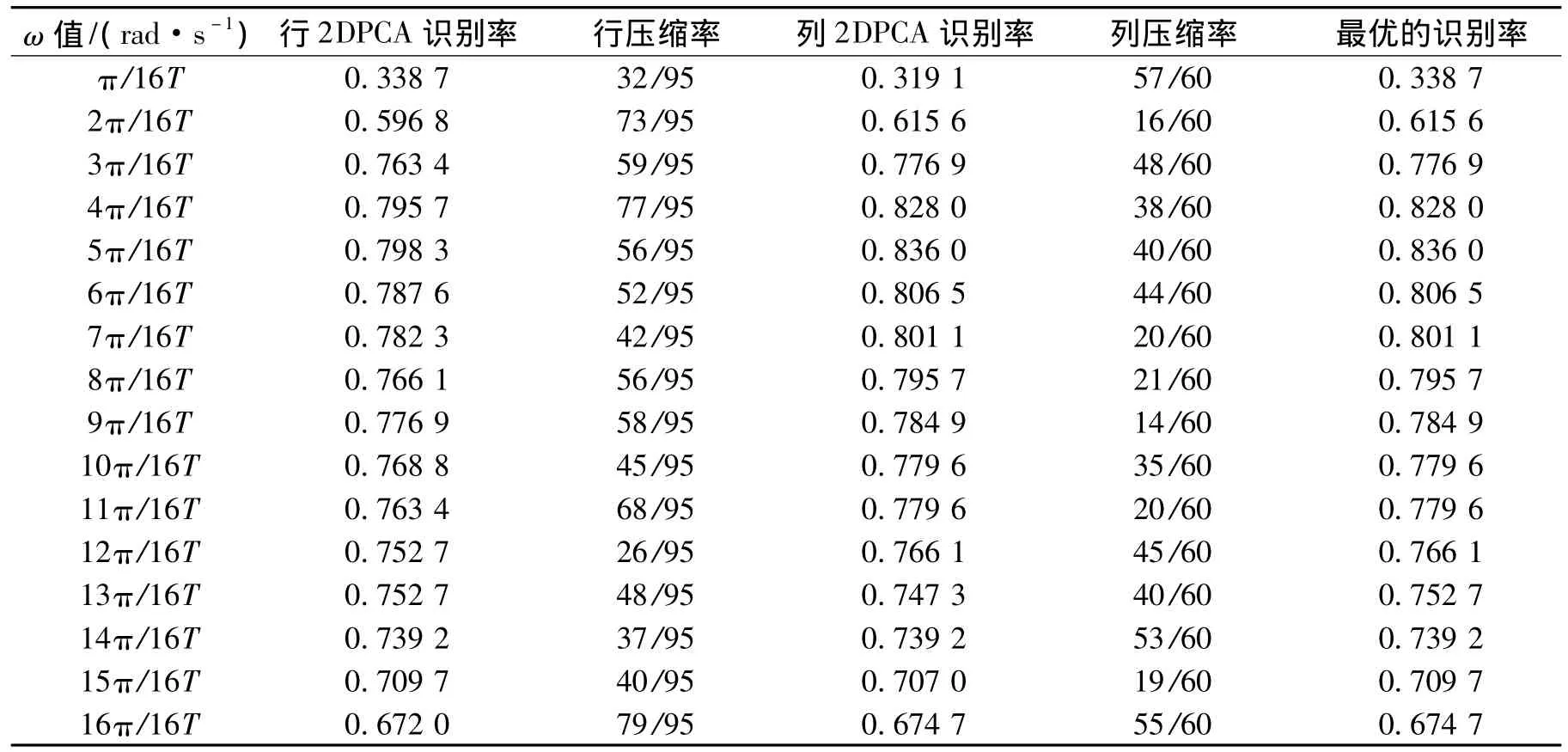
表1 ω值的选取对识别性能的影响Table 1 Different ω-value and recognition accuracy

当ω=5π/16T时有最好的识别率为0.836 0.其次是 ω 值为5π/16T、6π/16T、7π/16T和8π/16T.该值的选取与人行走的速度有关，人在正常步速时选取上述的5个ω时应该能获得较好的识别效果.实际上，式(2)相当于傅里叶变换中的基函数，而且式(1)是“拟傅里叶变换”，只不过Q(ω，t)的模值不恒为1.

Q(ω，t)的幅频特性如图4所示，其中图4(b)为图4(a)的局部放大图.令θ=ωt，图4(b)为ω=5π/16T时的Q(ω，t)的幅频特性，那么当 ω 值越大，类似频谱的频带越窄;反之，当ω值越小，类似频谱的频带越宽.频带适中时，识别效果较好.如表1所示，比较行、列2种2DPCA算法的识别率，总体来说，进行该 Radon变换特征的数据压缩时，列2DPCA好于行2DPCA方法.因此下面的实验直接采用列2DPCA.

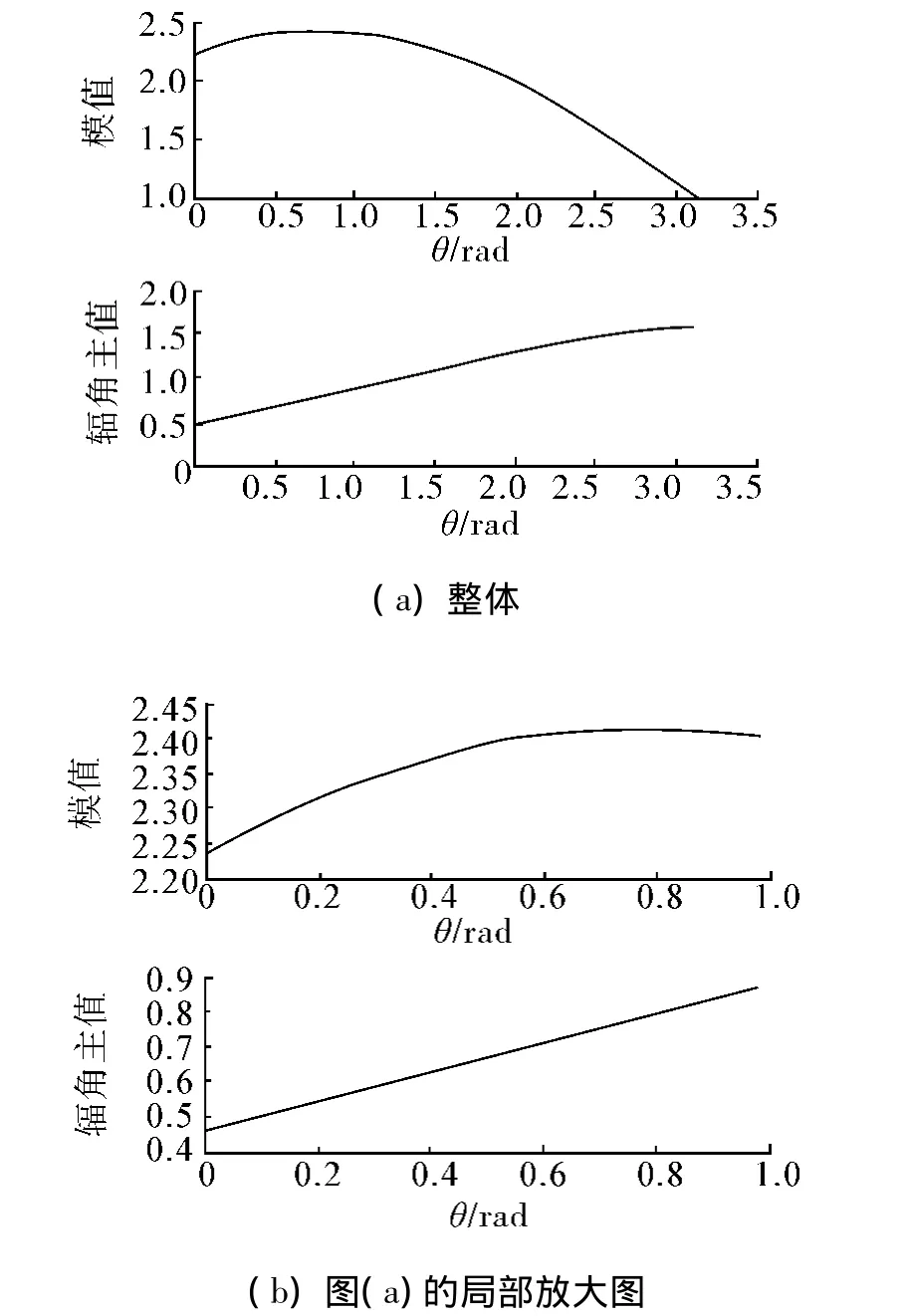
图4 模值与辐角主值特性图Fig.4 Characteristic graph of module value and argument principal value

3.3 θ的选取

在 CPU 3.06 GHz、内存 1 GB，VC++6.0 与Matlab 7.0混合环境下实验.现在选择Radon变换中参数 θ，θ∈［0°，180°)，为了能够获得最好的识别效果，考虑到180的质因数为2、3和5，因此θ所隔的角度为 4°、6°、9°、10°、12°、15°…，所提取到的特征只可能是 θ每隔 2°、3°、5°所提取到的特征的一部分.为了尽可能多地提取Radon变换的特征，在θ的间隔分别为2°、3°和5°上实验，实验结果如表2所示.由于步态数据库有124×6个样本，当θ从0°～180°(180°除外)每隔 3°取一次，共取 60 个 θ，总的Radon变换的特征提取时间为9 min，平均到每个样本的时间大约为0.73 s;若θ每隔2°取一次，共取90个θ，总的时间为16 min，平均到每个样本的时间大约为1.37 s;若 θ每隔5°取一次，共取36个 θ，总的时间为7 min，平均到每个样本的时间大约为0.56 s.当样本足够多时，这种特征提取所耗费的时间差异就相当可观.

表2 Radon变换中θ的选取对识别性能的影响Table 2 Different θ-value in Radon transform and recognition accuracy

由表2可以看出:最佳的识别率为0.836 0，出现在ω=5π/16T且θ的间隔为3°和5°.Radon变换时，θ的间隔为2°的特征维数多于θ间隔为3°和5°的，其识别率不及后两者，原因是θ间隔为3°和5°包含对识别有用的信息多.综合特征提取的时间以及识别性能:确定选取θ间隔为5°，特征模板的频率为ω=5π/16T.

最后，在Radon变换参数θ间隔为5°、特征构造模板中ω=5π/16T的参数下，对所提出的算法与文献［11］提出的基于关键帧的傅里叶描述子(KFD)方法进行比较，在同样的数据环境下实验，文献［11］的识别率仅仅为0.75，并且该方法的计算复杂度与所提出的算法的计算复杂度相当，都是比较容易实现的方法，计算量都比较小.

4 结束语

本文通过对步态序列图像进行Radon变换，构造一个步态周期的特征模板，它同时刻画了人体的静态结构信息和步态运动特征，将个体的步态特征用一幅图像来表达，直接对这个图像矩阵进行特征压缩，克服了传统PCA的不足，该方法简单易行，而且获得了令人鼓舞的识别效果.尽管如此，该方法是基于图形投影得到的特征，故受视角变化、行人衣着以及背包的影响较大.因此寻找减小外套变化以及视角变化对识别性能的影响的方法是下一步的工作重点.

致 谢

中科院自动化所为试验提供了免费的CASIA步态数据库，在此对中科院自动化所表示衷心的感谢.

［1］王科俊，侯本博.步态识别综述［J］.中国图象图形学报，2007，12(7):1152-1160.WANG Kejun，HOU Benbo.A survey of gait recognition［J］.Journal of Image and Graphics，2007，12(7):1152-1160.

［2］WANG Liang，TAN Tieniu.Automatic gait recognition based on statistial shape analysis［J］.IEEE Transcations on Image Processing，2003，12(9):1120-1131.

［3］URTASUN R，FUA P.3D tracking for gait characterization and recognition［C］//Proceedings of the 6th International Conference on Automatic Face and Gesture Recognition.Seoul，Korea，2004:17-22.

［4］黄凤岗，韩雪花.基于Radon变换的特征提取在步态识别中的应用［J］.哈尔滨工程大学学报，2007，28(3):301-304.HUANG Fenggang，HAN Xuehua.Feature extraction based on Radon transform for gait recognition［J］.Journal of Harbin Engineering University，2007，28(3):301-304.

［5］BOULGOURIS N V，CHI Z X.Gait recognition using Radon transform and linear discriminant analysis［J］.IEEE Transation on Image Processing，2007，16(3):731-740.

［6］王科俊，陈薇.基于Radon变换的步态识别系统［C］//全国模式识别学术会议.北京，2007:223-228.WANG Kejun，CHEN Wei.Feature extraction based on Radon transform for gait recognition［C］//Chinese Conference on Pattern Recognition.Beijing，2007:223-228.

［7］YANG Jian，ZHANG DAVIED，FRANGI A F，et al.Twodimensional PCA:a new approach to appearance-based face representation and recognition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(1):131-137.

［8］王科俊，贲晛烨，赵玥.步态识别中的步态检测与序列预处理［J］.自动化技术与应用，2009，28(8):69-72，79.WANG Kejun，BEN Xianye，Zhao Yue.Gait detection and sequence preprocessing for gait recognition［J］.Techniques of Automation and Applications，2009，28(8):69-72，79.

［9］王科俊，贲晛烨，刘丽丽.基于Fan-Beam映射的步态识别算法［J］.哈尔滨工业大学学报，2008，40(增刊):151-155.WANG Kejun，BEN Xianye，LIU Lili.Gait recognition based on fan-beam projection［J］.Journal of Harbin Institute of Technology，2008，40(Suppl.):151-155.

［10］王科俊，贲晛烨，孟玮，等.基于广义主成分分析的步态识别算法研究［J］.哈尔滨工程大学学报，2009，30(9):1022-1028.WANG Kejun，BEN Xianye，MENG Wei，et al.Research on a gait recognition algorithm based on generalized principal component analysis［J］.Journal of Harbin Engineering University，2009，30(9):1022-1028.

［11］YU Shiqi，WANG Liang，HUANG Kaiqi，et al.Gait analysis for human identification in frequency domain［C］//Proceedings of 3rd International Conference on Image and Graphics.Hong Kong，China，2004:282-285.