PCD型自适应弹性网络在微阵列分类中的应用

李钧涛，贾英民

(北京航空航天大学第七研究室，北京 100191)

PCD型自适应弹性网络在微阵列分类中的应用

李钧涛，贾英民

(北京航空航天大学第七研究室，北京 100191)

针对癌症分类中的重要基因选择问题，提出了一种基于顺向坐标下降算法的自适应弹性网络.该自适应弹性网络通过引入数据驱动权重，在构建分类器的同时能自适应地成群选择基因，从而产生了一个稀疏的学习模型，增强了可解释性.此外，通过引入惩罚因子，顺向坐标下降算法被改进并有效地用于求解该自适应弹性网络.急性白血病分类实验结果验证了所提方法的有效性.

癌症分类;基因选择;弹性网络;顺向坐标下降算法(PCD算法);微阵列分类

基于微阵列基因表达数据的癌症分类问题开辟了机器学习方法在计算生物领域的最早应用，大量的学习机器及求解算法已经被提出［1－15］.由于生物学家和医学科学家能从选择的重要基因来确定癌症研究中的最新发现或建议新的探索途径;因此，除了预测给定肿瘤样本的癌症类型，另一个挑战性的问题是辨识分类相关的重要基因［4－13］.

基因选择的目标是更好地理解产生数据的生物系统并改进分类器的预测性能.现流行的基因选择方法有:单变量排序［1］、判别式比率、主元分析、递归特征消除［2］等.然而，在这些方法中，基因选择与分类器构造是分开进行的.最近的统计学习理论与实验表明，同时进行基因选择和分类预测将产生优越的性能.因此，大量的新型学习模型被发展，例如1－范数支持向量机［3］、稀疏逻辑回归［4－5］、LASSO［6］.然而，这些学习方法并不能揭示基因间的相互信息，并且选择的基因个数以样本尺寸大小为上界.

从生物医学的角度考虑，癌症是一种复杂的遗传性疾病，不是由单个基因所决定的，而往往是由先天的或外界的影响所造成的一些基因的突变、缺失等原因所引起.因此，癌症分类中必然存在一些高度相关的基因，它们应该作为一个基因群，同时被选择或消除.从学习的角度，这可以被描述为一种群体效应，即对高度相关的基因表达列产生相似大小的估计系数.作为一种新的正则化方法，弹性网络［7］及其各种推广［8－9］能在构建分类器的过程中激励一种群体效应.然而，微阵列数据中往往含有数千个，甚至数万个基因表达列，而且重要基因对应的基因表达列可能与一些不重要基因表达列相关.因此，根据基因表达列相关性来激励群体效应将有可能导致最终模型包含冗余的基因.如何消除被选择群内的冗余基因是当前癌症分类中的一个急需解决的问题.

在弹性网络中，基因选择是由弹性网络惩罚的收缩自动获得的.因此，引入用于评估基因重要性的数据驱动权重到L1－范数惩罚和L2－范数惩罚将会自适应地控制着惩罚项的收缩，从而取得改进的基因选择性能［10－11］.受 LARS 型自适应弹性网络［10］和顺向坐标下降算法的启发，本文提出了一种基于顺向坐标下降算法的自适应弹性网络.该自适应弹性网络的一个突出优点是能自适应地成群选择基因.此外，该自适应弹性网络能利用改进的顺向坐标下降算法求解，大大提高了求解速度.将基于顺向坐标下降算法的自适应弹性网络应用到急性白血病分类中去，取得较满意的结果.

1 问题陈述

给定一个训练样本集{(xi，yi)}，其中xi=(xi1，xi2，…，xip)T是输入向量，yi∈{+1，－ 1}是样本标签，分类问题就是学习一个判别规则f:Rp→{+1，－1}，从而可以准确地预测新样本的标签.对于微阵列表达数据，xi表示具有p个基因表达水平的第i个样本，yi表示肿瘤类型.令y=(y1，y2，…，yn)T是响应向量，X=(x(1)，x(2)，…，x(p))是由n个输入向量按行排列组成的模型矩阵，其中x(j)=(x1j，x2j，…，xnj)T被称为预测子.假设预测子是标准化的，响应具有零均值，即

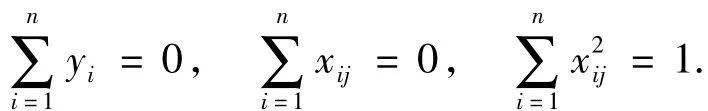
根据通常的线性回归模型［12］，输出响应能被预测为

式中:=(，…)T是被估计的系数向量.目标是:1)准确地预测新样本的标签;2)选择分类相关的重要基因.

对于基于微阵列基因表达数据的癌症分类问题，大量的学习机器已经被成功构建，例如，支持向量机［2－3］、稀疏逻辑回归［4－5］和弹性网络［7］.这些学习机器能被统一地归纳为正则化框架:

式中:λ ＞0是正则化参数;L(y，f(x))和J(λ，β)分别表示损失函数与惩罚，常用的损失函数有hinge损失、平方误差损失、指数损失等，常用的惩罚有L1－范数惩罚、L2－范数惩罚、弹性网络惩罚、SCAD惩罚等.结合弹性网络惩罚与平方误差损失，下面的弹性网络模型被提出［7］:

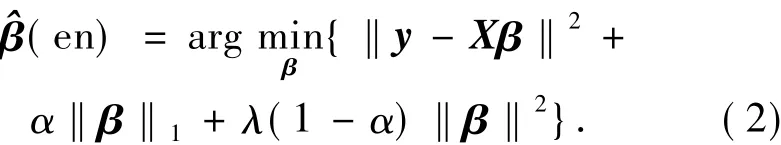
式中:λ＞0，1＞α＞0是新的模型参数.在固定α的前提下，顺向坐标下降算法可以用来迅速地求解弹性网络.

2 PCD型自适应弹性网络

作为一种新的正则化与变量选择方法，弹性网络能产生一个稀疏的统计学习模型，并能鼓励一种群体效应.虽然弹性网络弹极其推广已经被成功地应用于癌症分类和基因选择，然而该方法并不区分选择的基因群里基因的重要性，从而导致滤波模型中将包含冗余的基因.在本节中，将发展一种新型的统计学习工具来解决该问题.

2.1 统计模型

对于弹性网络(1)或(2)，相同的权重1被加在惩罚项的不同的系数上.理想的状况应该是大的惩罚加在不重要的变量上，从而很容易地消除它，而小的惩罚被强加在重要的变量上，从而在模型中保持它.基于上述思想，提出自适应弹性网络惩罚的概念.

给定训练集(xi，yi)，i=1，2，…，n，假设一个初始估计子=(，，…，)可以获得.不失一般性，进一步假设预测子x(1)，x(2)，…，x(p)被恰当排序，从而使得

为简便起见，仍旧用X表示变换后的模型矩阵.由于的度量在某种程度上暗示基因j对分类器的贡献，因此||(j=1，2，…，p)能被用来粗略地评估基因的重要性.根据这个粗略的评价标准，提出如下数据驱动权重矩阵:

式中:wj=||－1，通过引入权重系数，提出如下自适应弹性网络惩罚:

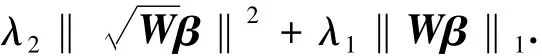
除了改进基因选择性能，提出自适应弹性网络(3)的另一个动机是其能用顺向下降算法求解(详见2.3小节)，从而大大减少了计算量.为了和其他类型的自适应弹性网络加以区别，把该学习机器命名为PCD型自适应弹性网络.使用该学习机器必须首先确定一个初始估计子.随着机器学习算法的快速发展，LASSO估计子、支持向量机的估计系数与弹性网络估计子都可以很方便地求解，从而被用作初始估计子.考虑到这些方法都不可避免模型参数选择的困难，从而需要花费大量的计算和时间来确定正则化参数和核参数.因此使用如下的单变量回归估计子作为初始估计子.

2.2 自适应的基因选择

由于重要基因可能与一些不重要的基因相关，因此弹性网络的滤波模型中可能会包含冗余的基因.PCD型自适应弹性网络能鼓励一种自适应的群体效应，从而能消除一些不重要的基因.

定理假设预测子x(1)，x(2)，…，x(p)是标准化的，响应y具有零均值.对于 1≤j，l≤p，如果aen)(aen)＞0，那么有

证明 令

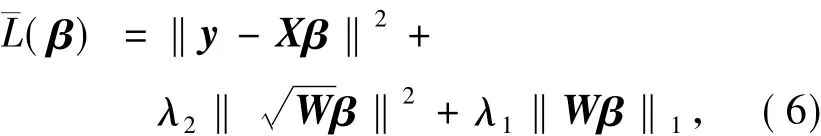
由于式(4)是一个无约束的凸最优化问题，因此式(6)对非零系数≠0的子梯度满足:

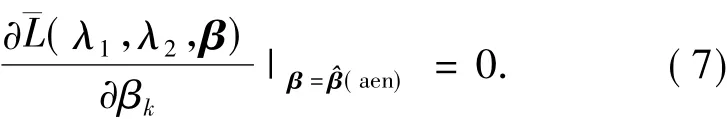
对于≠0，由式(7)可得

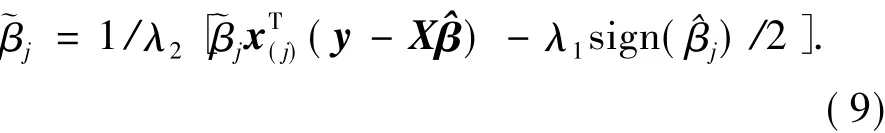
类似地，可得

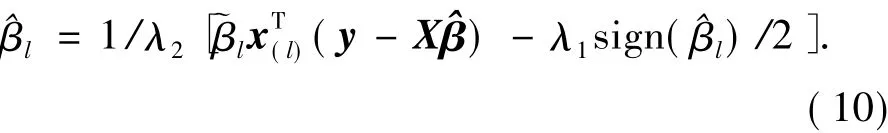
由于(aen)(aen)＞0且(aen)=(1+λ2)，因此sign()=sign().由式(9)减去式(10)可得

由式(4)和式(6)可得

从而

由于x(1)，x(2)，…，x(p)是标准化的，因此很容易可得

由式(11)、(12)和(13)，可得

把式(3)代入式(14)可得式(5).证毕.

利用最小二乘回归估计子(ols)作为初始估计子，Ghosh在2007年提出如下的自适应弹性网络［18］:

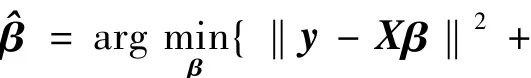
式中:wj=|(ols)|－γ，γ ＞0是提前给定的常数.利用弹性网络(en)作为初始估计子并引入比例系数，Zou在2009年提出如下的自适应弹性网络［19］:

式中:wj=|(en)|－γ，γ ＞0是提前给定的常数.虽然Ghosh的自适应弹性网络宣称能激励一种群体效应.然而所描述的群体效应控制上限是涉及2个正则化参数的复杂式子，缺乏直接的生物可解释性.因此，严格意义讲，这2种学习机器不具有可解释的群体变量选择功能.提出的PCD型自适应弹性网络能通过评估基因重要性来自动地辨识选择的基因群的尺寸，从而激励一种自适应群体选择效应.这种群体效应的上限是用乘式表达的，每一个乘子都具有较明确的生物学含义.

2.3 顺向坐标下降算法

类似于弹性网络，LASSO、LARS和前向阶梯等算法也能用来求解自适应弹性网络.然而，弹性网络和PCD型自适应弹性网络在增广空间中有p+n个观测子和p个预测子，而在微阵列基因表达数据中，一般说来p是非常大的，因此，这些算法将导致巨额的计算量，有时甚至是计算上不可行的.与这些方法相比较，顺向坐标下降算法在处理这类数据时具有不可争议的快速性.因此，选择使用该算法来求解PCD型自适应弹性网络.

为了计算简便的目的，把PCD型自适应弹性网络(3)改写为

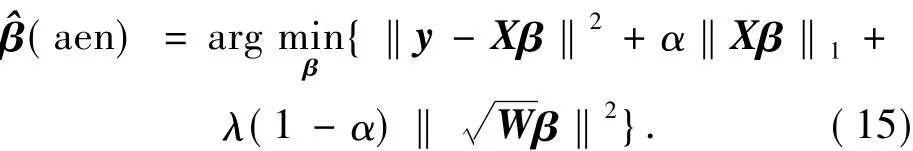
假设在l≠j时，估计子可以获得.目标是获得关于βj的部分最优化.根据文献［16］，坐标下降调整有如下形式:

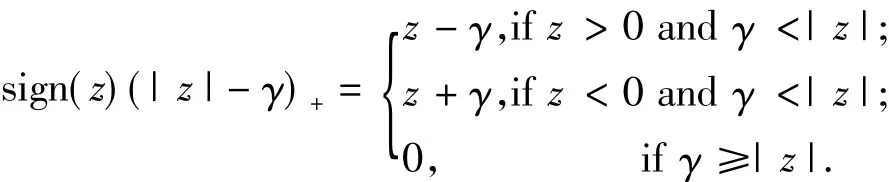
为了使用顺向坐标下降算法，必须首先选择1个最小的正则化参数值λmin，并构造1个从最大值λmax到最小值λmin对数下降的λ序列.典型的构造方法是令K=100，λmin=ελmax，其中 ε =0.001.如果使用自己构造的λ序列，那么不同的惩罚因子可以被加在每一个系数上，从而可以成功求解PCD型自适应弹性网络(15).具体求解步骤如下:

2)设置顺向坐标下降算法的初始参数值:响应类型、弹性网络混合参数α、最小λ值和惩罚因子等参数.

3)利用顺向坐标下降算法求解具有惩罚因子w1，w2，…，wp的弹性网络.

4)利用交叉检验决定最优模型的参数.

5)提取最优模型的非零系数来构建分类器，并确定非零系数对应的基因.

由于自适应弹性网络惩罚把一些系数收缩到零，因此在构建分类器的同时，实现了基因的自动选择，所需要做的是提取非零系数并决定与他们相对应的基因名称.在实验中，上述算法程序是用R语言写的，但在执行该程序时，需要加载并使用“glmnet”工具包.R程序中的函数“as.character”被用来产生并测试基因性状，函数“predict”和“coef”被联合使用，从而提取估计模型中的非零系数.

由于相同的数据驱动权重被同时加在1－范数惩罚系数和2－范数惩罚系数上，所以提出的自适应弹性网络可以用带惩罚因子的顺向坐标下降算法来求解.在Ghosh和Zou自适应弹性网络中，由于仅有1－范数惩罚系数被赋予于权重，因此无法用该算法来求解.

3 仿真实验与分析

白血病基准数据被用来验证所提方法的有效性.该基准数据包含47个急性淋巴性白血病样本和25个急性骨髓性白血病样本，其中，每一个样本包含7 129个基因表达值.实验的目的是:构建诊断规则，区分这2种急性白血病.基准数据的训练集中包含27个急性淋巴性白血病样本和11个急性骨髓性白血病样本，余下的34个样本用来测试诊断规则的预测精度.为了能使用回归模型来处理二分类问题，把白血病编码为 0－1影响，并定义分类函数为I(＞0.5)，其中I(·)是指示函数.

第1个实验评估了弹性网络和PCD型自适应弹性网络的预测性能.为此，给定的72个样本数据被随机地划分成10个部分，使得每一部分所含样本个数基本相等，然后计算这2种学习机器的10重交叉检验均方预测误差，并以此来评估他们的预测性能.图1给出了这2种学习机器的交叉检验预测误差曲线.由图1易知，PCD型自适应弹性网络能明显改进弹性网络的预测性能.这种现象可以从基因选择的角度给出解释.在基准白血病数据中，基因M23197_at、M27891_at和 M63138_at具有高度相关的表达列，并且这些表达列和基因M31303_rnal_at的表达列高度负相关;因此这4个基因在弹性网络和PCD型自适应弹性网络中，被作为一个基因群被同时选择.基因 M22324_at的表达列与基因M92287_at和X74262_at的表达列高度负相关;因此，这3个基因作为一个基因群被弹性网络同时选择.然而，基因M22324_at并不对分类产生很大影响，PCD型自适应弹性网络通过评估基因重要性，把不重要基因M22324_at从该群中消除出去.这种自适应的群体基因选择解释了PCD自适应弹性网络取得好的预测精度的原因.

图1 10重交叉检验预测误差曲线Fig.1 Curve of tenfold cross－validated prediction error

第2个实验比较了LARS算法和顺向坐标下降算法的运算速度.在配置为 Pentium(R)D CPU 3.4 GHz，3.39 GHz、内存1.00 GB的双核戴尔计算机上，利用LARS算法求解100步的弹性网络［7］和LARS型自适应弹性网络［10］大约需要2～3 min;而用顺向坐标下降算法求解K=100的PCD型自适应弹性网络，只需要30 s左右.

4 结束语

PCD型自适应弹性网络通过引入恰当的权重，改进了弹性网络的基因选择、计算速度等性能.与Ghosh自适应弹性网络、Zou自适应弹性网络等统计学习模型相比，PCD型自适应弹性网络更能激励一种群体基因选择效应.与LARS型自适应弹性网络相比，PCD型自适应弹性网络能大大提高了计算速度.本文仅使用1个微阵列数据集来验证PCD型自适应弹性网络的有效性，因此在更多的数据集上来检验其性能并给出其合理的生物学解释是接下来要做的工作.

［1］GOLUB T R，SLONIM D K，TAMAYO P，et al.Molecular classification of cancer:class discovery and class prediction by gene expression monitoring［J］.Science，1999，286(5439):531－536.

［2］GUYON I，WESTON J，BARNHILL S，VAPNIK V.Gene selection for cancer classification using support vector machines［J］.Machine Learning，2002，46(1):389－422.

［3］ZHU J，ROSSET S，HASTIE T，TIBSHIRANI R.1－norm support vector machines［J］.Advances in Neural Information Processing Systems，2004，16(1):49－56.

［4］SHEVADE S K，KEERTHI S S.A simple and efficient algorithm for gene selection using sparse logistic regression［J］.Bioinformatics，2006，19(17):2246－2253.

［5］CAWLEY G C，TALBOT N L C.Gene selection in cancer classification using sparse logistic regression with Bayesian regularization［J］.Bioinformatics，2006，22(19):2348－2355.

［6］TIBSHIRANI R.Regression shrinkage and selection via the lasso［J］.Journal of the Royal Statistical Society:Series B，1996，58(1):267－288.

［7］ZOU Hui，HASTIE T.Regularization and variable selection via the elastic net［J］.Journal of the Royal Statistical Society:Series B，2005，67:301－320.

［8］WANG Li，ZHU Ji，ZOU Hui.The doubly regularized support vector machine［J］.Statistica Sinica，2006，16(2):589－615.

［9］李钧涛，贾英民.用于微阵列分类的Huberized多类支持向量机［J］. 自动化学报，2010，36(3):399－405.

LI Juntao，JIA Yingmin.Huberized multi－class support vector machine for microarray classification［J］.Acta Automatica Sinica，2010，36(3):399－405.

［10］李钧涛，贾英民.用于癌症分类与基因选择的一种改进的弹性网络［J］. 自动化学报，2010，36(7):976－981.

LI Juntao，JIA Yingmin.An improved elastic net for cancer classification and gene selection［J］.Acta Automatica Sinica，2010，36(7):976－981.

［11］LI Juntao，JIA Yingmin，DU Junping，YU Fashan.A new support vector machine for microarray classification and adaptive gene selection［C］//2009 American Control Conference.St.Louis，USA:5410－5415.

［12］EGAL M，DAHLQUIST K，CONKLIN B.Regression approaches for microarray data analysis［J］.Journal of Computational Biology，2003，10(6):961－980.

［13］VAPNIK V.The nature of statistical learning theory［M］.New York:Springer，1995:1－60.

［14］EFRON B，HASTIE T，JOHNSTON I，TIBSHIRANI R.Least angle regression［J］.Annals of Statistics，2004，32(2):407－499.

［15］陈晓峰，王士同，曹苏群.半监督多标记学习的基因功能分析［J］. 智能系统学报，2008，3(1):83－90.

CHEN Xiaofeng， WANG Shitong， CAO Suqun.Gene function analysis of semi－supervised multi－label learning［J］.CAAI Transactions on Intelligent Systems，2008，3(1):83－90.

［16］FRIEDMAN J，HASTIE T，TIBSHIRANI R.Regularization paths for generalized linear models via coordinate descent［R］.Palo Alto，USA:Standford University，2008.

［17］FRIEDMAN J，HASTIE T，HÓFLING H，TIBSHIRANI R.Pathwise coordinate optimization［J］.Annals of Applied Statistics，2007，1(2):302－332.

［18］GHOSH S.Adaptive elastic net:an improvement of elastic net to achieve oracle properties:IUPUI tech report No.pr07－01［R］.Indianapolis，USA:Department of Mathematical Sciences，Indiana University－Purdue University，2007.

［19］ZOU H，ZHANG H H.On the adaptive elastic net with a diverging number of parameters［J］.Annals of Statistics，2009，37(4):1733－1751.

李钧涛，男，1978年生，讲师、博士.主要研究方向为智能控制、统计学习及其在生物信息学中的应用.

贾英民，男，1958年生，教授、博士生导师，教育部“长江学者”特聘教授，中国科学院系统控制重点实验室学术委员会委员，中国人工智能学会智能空天系统专业委员会主任，中国自动化学会控制理论专业委员会副主任，中国航空学会控制理论与应用专业委员会副主任.主要研究方向为鲁棒控制、自适应控制、智能控制及其在车辆系统和工业过程中的应用.承担国家“973”计划、“863”计划，国家自然科学基金重点项目、科学仪器专项，面上项目，国防基础科研项目，教育部高校博士点基金等20余项.国家杰出青年科学基金获得者，国家“百千万人才工程”第一、二层次人选.发表学术论文120余篇，出版专著1部，申请专利10余项.

Applying a PCD adaptive elastic net in microarray classification

LI Jun－tao，JIA Ying－min
(The Seventh Research Division，Beihang University，Beijing 100191，China)

An adaptive elastic net was proposed，based on a pathwise coordinate descent(PCD)algorithm，to select genes important for cancer classification.By introducing data－driven weights，the proposed adaptive elastic net can adaptively select genes in groups in the process of building classifiers.It thus produces a sparse learning model with enhanced interpretability.Furthermore，by introducing penalty factors，the pathwise coordinate descent algorithm was improved，solving the adaptive elastic net more efficiently.Experimental results from leukemia classification verified the proposed method.

cancer classification;gene selection;elastic net;pathwise coordinate descent algorithm;microarray classification

TP273

A

1673－4785(2010)03－0227－06

10.3969/j.issn.1673－4785.2010.03.004

2009－12－14.

国家自然科学基金资助项目(60727002，60774003，60850004);国家“973”计划资助项目(2005CB321902);国防基础研究资助项目(A2120061303).

李钧涛.E－mail:juntaolimail@yahoo.com.cn.