含裂纹曲轴的有限元模态分析

尹长城，孙玮琪

（湖北汽车工业学院 汽车工程系，湖北 十堰 442002）

曲轴是发动机的重要零部件之一，承受着复杂交变的冲击载荷。随着发动机的发展和强化，曲轴的工作条件也愈加苛刻，因而保证曲轴的工作可靠性是至关重要的。实际工作过程中，由于曲轴承受着周期性载荷力的作用，在发动机工作转速范围内可能会发生共振现象，导致动应力急剧增大，使得曲轴产生疲劳裂纹。疲劳裂纹会使材料应力水平急剧降低，导致曲轴在力的作用下很容易发生断裂。此时传统的静力学设计与经验设计已不能满足曲轴设计要求，动态特性分析是非常必要的。

裂纹不仅影响曲轴的使用寿命，严重时还会造成巨大的危险。因此，曲轴裂纹的动态监测和诊断技术受到国内外学者的广泛关注。目前裂纹诊断的研究是基于理论、有限元法、试验三方面进行的探讨［1－3］。本文利用有限元法建立含裂纹曲轴的计算模型进行分析，为曲轴动态监测提供有益参考。

1 曲轴几何模型的建立

曲轴结构形状复杂，如果采用有限元软件ANSYS建模需要相当大的工作量，而且势必对曲轴的几何模型进行大量的简化，会造成数值模拟失真。本文采用CATIA软件创建曲轴三维模型［4］，综合考虑计算机的求解能力、计算时间和计算精度，对曲轴模型进行了模型简化（图1）。忽略一些小圆角和油道孔、小肩台等实体修饰特征。

图1 曲轴几何模型

曲轴材料类型QT720—2，总长度为910 mm，主轴颈直径为75 mm，连杆轴颈直径为62 mm，曲柄宽度为116 mm。

2 无裂纹曲轴的自由模态分析

2.1 无裂纹曲轴的有限元模型

将基于CATIA V5创建的曲轴模型保存为model格式，将生成的model文件导入ANSYS 9.0环境中。设置曲轴的材料参数：密度为7.3×10－9t/mm3，杨氏模量E为1.73×105 MPa，泊松比为0.3。

对于曲轴的网格划分，采用SOLID45单元进行智能网格划分，划分网格后的得到单元数目为157445，节点数目为32639，曲轴有限元模型见图2。

图2 无裂纹曲轴的有限元模型

2.2 无裂纹曲轴的自由模态分析

在ANSYS 9.0中进行曲轴的自由模态分析，利用Block Lanczos法提取模态［5］，三维实体结构在无约束的边界条件下的模态分析，计算出来的前6阶模态为刚体模态，其固有频率为零。真正有意义的模态从第7阶开始，前4阶非零模态的固有频率和振型描述如表1所示。

表1 曲轴自由模态分析结果

曲轴自由模态分析时，激活单元应力计算选项，获取曲轴各阶次模态应力图。非零的前4阶的模态应力图，如图3所示，虽然，应力值并没有实际意义，但是，如果振型是相对于单位矩阵归一化处理，则可以在给定的振型中比较不同点的应力，从而发现可能存在的应力集中。所以，通过它可以找出曲轴的应力集中部位，为后续曲轴的裂纹开口的选取提供依据。由图3可知，在曲轴主轴颈、连杆轴颈与曲柄、平衡块的结合处，这些部位的应力相对较大，是最容易产生疲劳裂纹的地方。这与曲轴在服役阶段出现疲劳裂纹的部位相同。

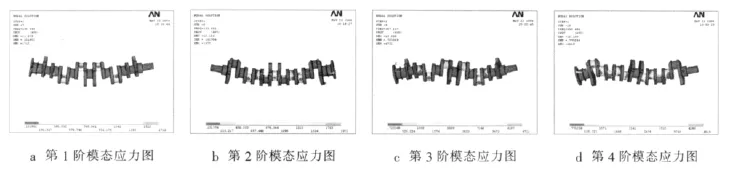
图3 前4阶非零模态应力图

3 含裂纹曲轴的自由模态分析

针对曲轴裂纹的模拟在国内外研究资料中一般采用2种方法，一种是采用TimoshenkoL梁单元模拟裂纹［1，3］，该方法从断裂力学推演裂纹梁单元格式，并考虑梁单元的转动惯量和剪切效应。另一种方法则采用削弱轴的尺寸来实现［2］，此方法基于连续介质力学有限元法理论，认为微小裂纹不影响曲轴的质量，只是刚度矩阵发生变化，从而导致系统的固有频率发生变化。本文采用第2种方法模拟裂纹。

无裂纹曲轴的自由模态分析结果可知，在曲轴中间位置处的主轴颈和平衡块的结合处的应力最大，选择在此处开设裂纹，其相对深度C（裂纹深度/主轴颈半径）为0.1～0.9的不同深度的横向裂纹，如表2所示。

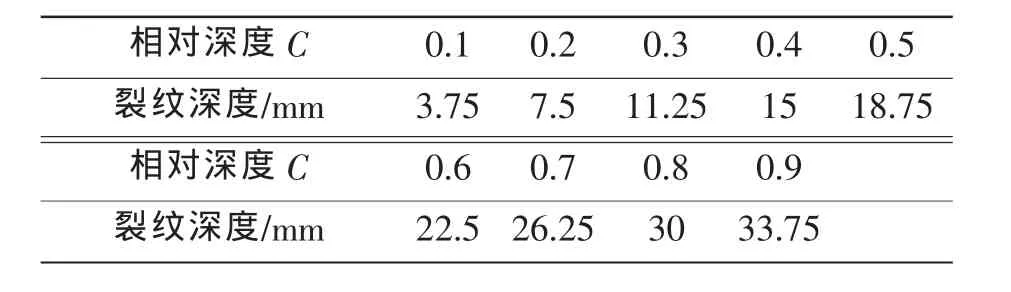
表2 曲轴裂纹深度范围

对含裂纹曲轴进行自由模态分析，其曲轴材料属性和网格密度设置与无裂纹的情形相同。表3给出裂纹相对深度为0.1的曲轴前4阶非零固有频率值以及相应的振型。其振型图如图4所示。

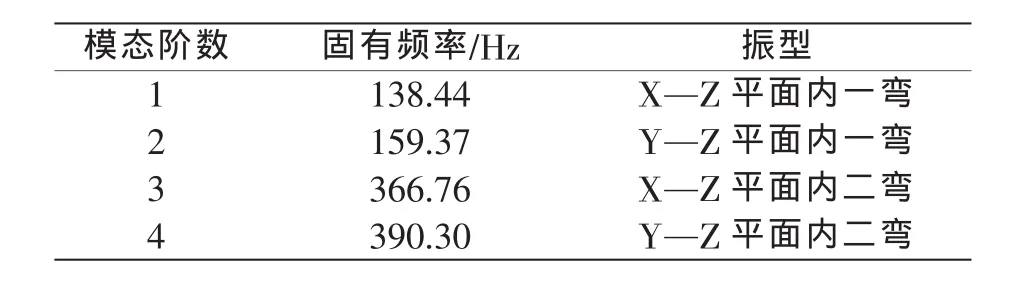
表3 裂纹相对深度0.1的曲轴模态分析结果

由表3可知，当曲轴含裂纹时，其同阶固有频率降低。且含裂纹曲轴的振型与无裂纹曲轴的振型一致，曲轴中的裂纹并不会改变曲轴的自振形式。表4列出不同深度裂纹曲轴固有频率的计算结果。

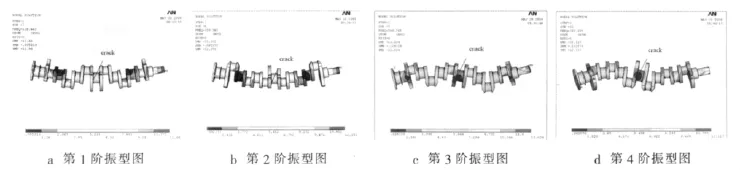
图4 含裂纹曲轴前4阶非零振型图

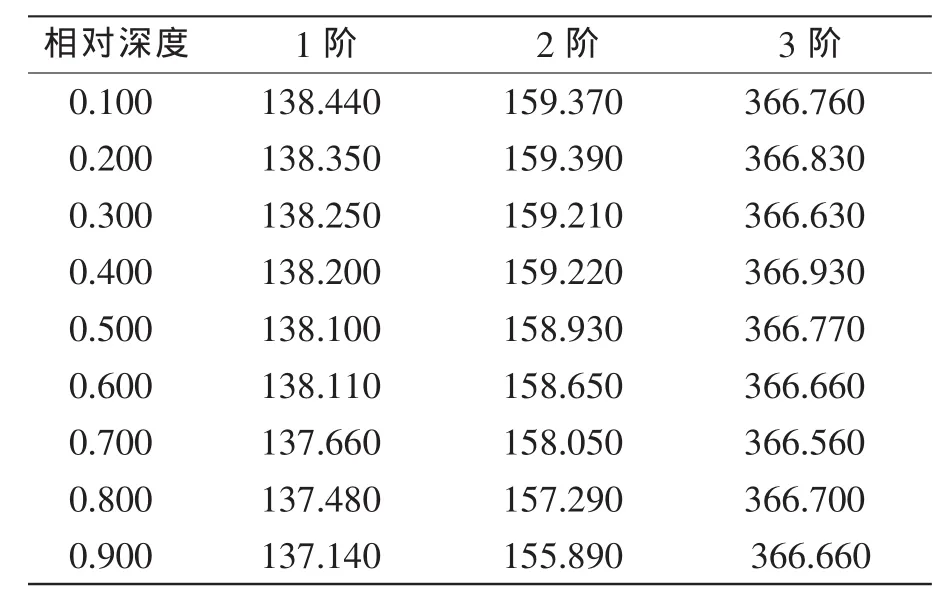
表4 不同深度裂纹曲轴的固有频率

对比表1和表4的数据可知，当曲轴存在裂纹时，曲轴的固有频率降低。一般来说，随着裂纹越来越深，固有频率降低的越来越大。但是，不同阶次的曲轴固有频率变化趋势不一样。低阶固有频率的变化比较大 （尤其是2阶固有频率变化最为显著），而高阶固有频率的变化比较平缓。

4 结 论

1）曲轴上含裂纹时，其固有频率降低，但不改变曲轴的自振形式。

2）随着裂纹越来越深，固有频率变化越来越大，尤其是低阶情况比较明显。

3）利用有限元法计算含裂纹曲轴的固有频率，在计算机中开设曲轴裂纹比较方便，是一种有效的方法，可代替大量的试验。

4）从模态分析入手，可确定曲轴是否含有裂纹，但由于曲轴的形状复杂，不能检测到曲轴裂纹的存在位置。

［1］ Papadopoulos C A， Dimarogonas A D.Coupled longitudinal and bending vibrations of a rotating shaft with an open crack ［J］.Journal of Sound and Vibration，1987，117（1）：81－93.

［2］ 孙 倩，赵国文.基于CAD建模的单缸曲轴裂纹的有限元模态分析［J］.舰船科学技术，2008（2）：157－160.

［3］ 雷宣扬，宋希庚，薛冬新.含裂纹曲轴的振动特性分析［J］.农业机械学报，2003（6）：183－185.

［4］ 李学志，李若松.CATIA实用教程［M］.北京：清华大学出版社，2004.

［5］邢静忠，王永岗，陈晓霞，等.ANSYS 7.0分析实例与工程应用［M］.北京：机械工业出版社，2004.