简支梁振动可靠性的Monte Carlo模拟
莫文辉
(湖北汽车工业学院 机械工程系,湖北 十堰442002)
国外学者研究了结构线性振动、非线性振动的可靠性[1-3]。 文献[4]提出了单自由度系统振动可靠性计算的一种方法,导出了固有频率和激振频率的正态联结方程。文献[5]提出了一种进行构件振动可靠性设计的方法,建立了激振力频率与构件固有频率干涉的概率模型,给出了将导致构件损坏的强迫共振响应的概率计算公式。文献[6]把悬臂梁的固有频率、激振力频率、平均应力、应力辐和疲劳极限处理为随机变量,提出了悬臂梁在强迫振动时不发生共振和疲劳损坏的可靠性分析方法。文献[7]述及了整体离心叶轮的结构及其故障模式特点,在强迫振动放大系数模型的基础上,提出了离心叶轮叶片的振动可靠性分析方法,通过厚度控制来调整整体叶轮叶片的固有频率,控制强迫振动放大系数,使之避开危险性共振或强迫振动。
考虑随机因素对简支梁振动的影响,应用Monte Carlo模拟,研究了简支梁振动的可靠性。
1 简支梁的振动分析[8]
简支梁的跨度中点有一台重量为Q的电动机,其转子以角速度ω转动。转子偏心所引起的离心惯性力为Fi,其垂直分量Fisin ωt即为周期性变化的干扰力,从而引起梁的横向强迫振动。Fi的水平分量Ficos ωt引起梁的纵向振动,它的影响远小于横向振动,通常不进行计算。梁与电机所组成的系统的横向振动简化成一个自由度的振动系统。简支梁在静载荷Q作用下,静位移Δj为

故弹性常数为

由牛顿第二定律,得振动物体的运动方程为

其中 rx˙为阻力。 由于 KΔj=Q,化简式(3),得

由于系统的固有频率为


式(4)简化为

由微分方程理论知,当(2C)2-4p2<0,即 C 式(8)右边的第1部分为衰减振动,随时间增加迅速减弱,终于消失;第2部分则为强迫振动。在第1部分消失后,式(8)化为 其中B是强迫振动的振幅。 引入放大系数的记号 振幅B可写为 其中 简支梁跨度中点的最大挠度为 在线弹性范围内,材料服从虎克定律,则应力、载荷和变形之间成正比关系。梁在静平衡位置时的最大静应力σj与在最大位移位置时的最大动应力σdmax之间关系是 同理 故有 根据概率论的中心极限定理,当独立随机变量的个数增加时,其和的分布趋于正态分布。只要产生 12 个均匀分布随机数 u1、u2、…、u12,将其相加,再减去6,可近似地得到标准正态变量的样本值。这是产生标准正态变量的样本值的一种方法,使用此方法编程方便。 随机变量Xi服从数学期望μi,方差的正态分布,记为 Xi~N(μi,)。随机变量Z服从数学期望0、方差1的正态分布,记为Z~N(0,1)。 利用关系式 就得到一般的正态随机变量Xi。 Monte Carlo模拟在机械可靠度计算中的应用是从随机变量 X1、X2、…Xi、…、Xn分布中随机抽取一组数值,代入应力计算公式得到一个应力值,再与抽自强度分布的一个强度值进行比较,如果应力大于强度,则零件失效;反之,零件安全。设模拟次数为N,失效数为F,可靠度R为(1-F/N)。模拟次数愈大,则模拟精度愈高。就本文而言,应力指简支梁跨度中点的最大动应力。 已知简支梁跨度l为3±0.005 m,E为200±20 GN·m-2,I为 500000±10000 mm4。安装在跨度中点的电动机重量Q为12±0.1 kN,转子偏心所引起的惯性力 Fi为 2.5±0.025 kN,转速为 1500±30r·min-1。若不计梁的质量和介质的阻力(C=0),跨度中点最大许用振动位移均值为0.000675 mm,标准差为0.000001,强度均值为13.2 MPa,标准差为0.1。用VB 6.0编写计算机程序,模拟1000次,得出位移的可靠度为0.983,强度的可靠度为0.996。 建立简支梁振动的微分方程,求出最大振动位移和最大动应力。考虑随机因素对简支梁振动的影响,用计算机程序产生1000组随机变量样本,用Monte Carlo模拟研究了结构最大振动位移和最大动应力的可靠性。随着计算机CPU速度的提高,Monte Carlo模拟结构的可靠度是可行的。 [1] Y.K.Lin.Probabilistic Theory of Structural Dynamics[M].New York:McGraw-Hill,1967. [2] L.A.Bergman, J.C.Heinrich.On the Reliability of Linear Oscillator and Systems of Coupled Oscillators[J].Int.J.of Numerical Methods in Engrg., 1982,18:1271 -1295. [3] B.F.Jr.Spencer,I.Elishakoff.Reliability of Uncertain Linear and Nonlinear Systems [J].J.Engrg.Mech.,ASCE.,1988,114(1):135-148. [4] 何晓聪.单自由度系统振动可靠性计算方法初探[J].昆明理工大学学报,1998(2):52-54. [5] 王延荣,田爱梅.构件振动可靠性设计方法初探[J].航空动力学报,2003(2):32-35. [6] 史进渊.悬臂梁振动可靠性分析的研究[J].应用力学学报,1995(2):111-114. [7]金向明,高德平,蔡显新,等.整体离心叶轮叶片的振动可靠性分析[J].航空动力学报,2004(5):31-34. [8] 刘鸿文.材料力学(下册)[M].北京:高等教育出版社,1983. [9] 盛 骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2001. [10]卢玉明.机械零件的可靠性设计[M].北京:高等教育出版社,1989.

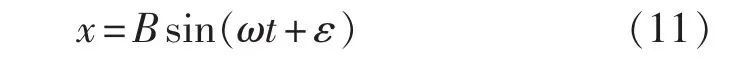







2 简支梁振动可靠性的Monte Carlo模拟
2.1 随机变量的模拟[9]

2.2 Monte Carlo模拟计算可靠度
2.3 算 例
3 结 论

