圆钢管空间滞回性能试验

聂桂波，支旭东，范 峰

(哈尔滨工业大学 土木工程学院，哈尔滨150090，nieguibo0323@163.com)

目前，空间网格结构在强震作用下的损伤累积过程及其失效机理研究逐渐深入［1-5］，其中材料本构模型研究与应用是重要工作.与多、高层结构的相关研究不同［6-9］，空间网格结构的构件主要以圆钢管为主，其在强震下失效时往往变形明显、材料塑性发展深入，体现了明显的强度破坏特征.文献［10-11］初步进行了考虑材料损伤累积对空间网格结构强震响应影响的研究，对比表明，考虑材料滞回损伤累积对结构的失效特征及失效极限具有明显影响，这种影响最大时可达20%以上.因此，要精确获得结构在地震下的响应规律，必须以更为准确的材料本构模型作为基础，这就要求对此类构件进行专门的试验研究，以准确掌握该类构件的空间滞回性能，从而获得精确适用的材料本构模型.

本文考虑空间复杂荷载特性以及不同长细比的影响，设计并进行了多组圆钢管试件的空间滞回性能试验，考察了该类构件的空间滞回性能，获得了滞回试验曲线及典型部位的应变过程数据结果，为深入研究确定符合圆钢管截面的钢材本构模型奠定了基础.

1 试验方案

1.1 试件设计

为获得圆钢管构件的滞回试验曲线及典型部位的应变曲线，考察其空间滞回性能，以空间结构工程中常用的圆钢管为试验对象，选取3 种高度和截面的试件，截面分别为φ 76，φ 114，φ 140，高度取900，1 200，1 500 mm，所有试件壁厚均为5 mm，试件将设计成悬臂支撑模式，所选试件的长细比参考了空间网格结构常用的长细比(试件及试验装置见图1).为使水平加载的加载器与管身相连，构件上端端部两个正交水平方向焊接耳板，允许加载器在竖直及水平面内有一定的转角;为增加试件的稳定性及刚度，试件底部焊接刚度较强的端板，预留栓孔与下部钢箱用高强螺栓连接.

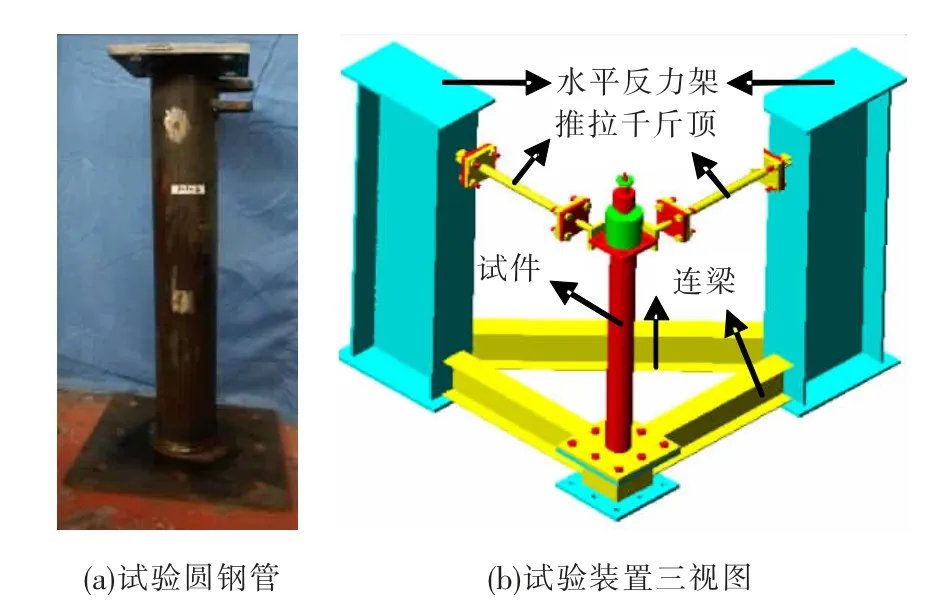
图1 试验装置及试件

1.2 加载装置及测点布置设计

水平向加载装置如图1(b)所示，考虑双向水平加载.试件顶部在两个相互垂直的水平方向均有侧移，所以将连接设计成铰接，保证两方向均可产生一定的旋转角度.水平反力架与钢管底部的钢箱用连梁连接，组成自平衡系统.

沿试件轴向加载的难度在于试件顶部既要承受竖向力，又要按照悬臂支撑要求保证试件顶部为自由端.为解决这一关键问题，进行了多种试验方案的对比，前期方案采用独立反力架上的反力梁承担竖向力，试图通过减小竖向千斤顶与反力梁接触部位的摩擦力达到使其在水平向滑动的目的.但前期多个试验方案的加载表明:

1)这些试验装置加工精度要求高，很难克服摩擦力，使接触部位顺利滑动.并且在后期试验数据处理过程中，尚应准确消除该处摩擦力的影响.

2)试验装置在试验过程中安装比较困难;在加载位移比较大的情况下，还会存在一定的安全隐患.

3)前期方案需要使用试验室的反力架，用以安装反力梁承担竖向力，反力架虽然在竖向的刚度足够，但水平向刚度薄弱，试验过程中承担竖向力的反力梁在加载过程中随水平荷载摆动，严重影响试验精度，其误差也难以消除.

最终确定的方案是:在试件的上下底板预留圆孔，然后将螺杆从孔中穿入，螺杆的底部用螺栓球与其拧紧，螺杆顶部放置钢筋拉拔器及力传感器，用钢筋拉拔器张拉螺杆产生拉力，从而反作用于钢管，达到施加轴力的目的，如图2(b)所示.该装置适用于三维损伤构件的加载，具有操作简单、便于安装调试和安全可靠的优点.

两水平加载器均布置了力传感器，水平加载器互相垂直，一路记为X 方向，另一路记为Y 方向，管顶两个方向均设位移计.试验过程中，在试件的典型部位布置测点，每个测点粘贴电阻应变片测量应变变化.测点在试件的3 个高度沿管径均匀布置，其编号及位置如图2(a)所示.

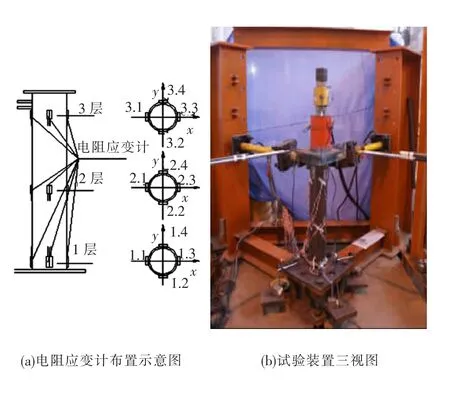
图2 试验装置及测点布置图

1.3 数据采集系统

试验竖向力采集通过YE2537 采集仪采集;水平力和位移分别通过力传感器及LVDT 位移计将数据传入到北京波谱仪中，北京波谱仪将测得的力与位移数据以图像的形式实时的显示出来，并每隔一定时间自动记录采集数据.典型部位的应变通过东华3816 应变采集系统采集.

1.4 加载方案和试件编号

加载方案见图3，试件编号见表1.

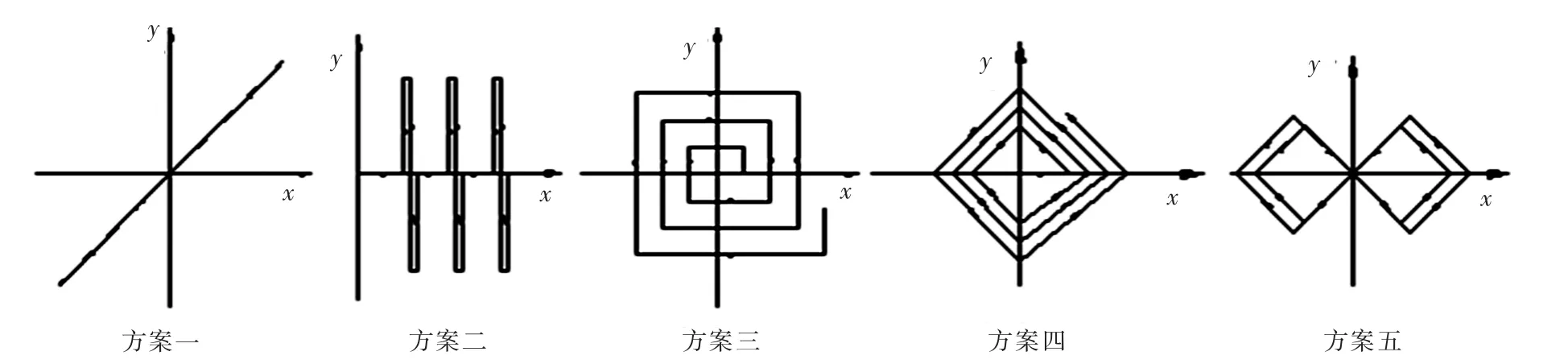
图3 加载方案

表1 试件编号

2 滞回试验结果

2.1 试验稳定性验证

为验证该试验装置及数据采集系统的稳定性，选取两组相同试验进行验证.每组3 根试件，分别采用加载方案1 和方案2，杆件编号见表2.限于篇幅，仅给出第二组试件Y 向滞回曲线，见图4.为便于比较，将相同加载方案试件的滞回曲线放在图5 中(图中隐去了破坏之前变形较大的部分，以利于对图形的观察)，各试件滞回曲线吻合较好，表明试验具有较高的稳定性，结果可信.

表2 对比试验试件编号

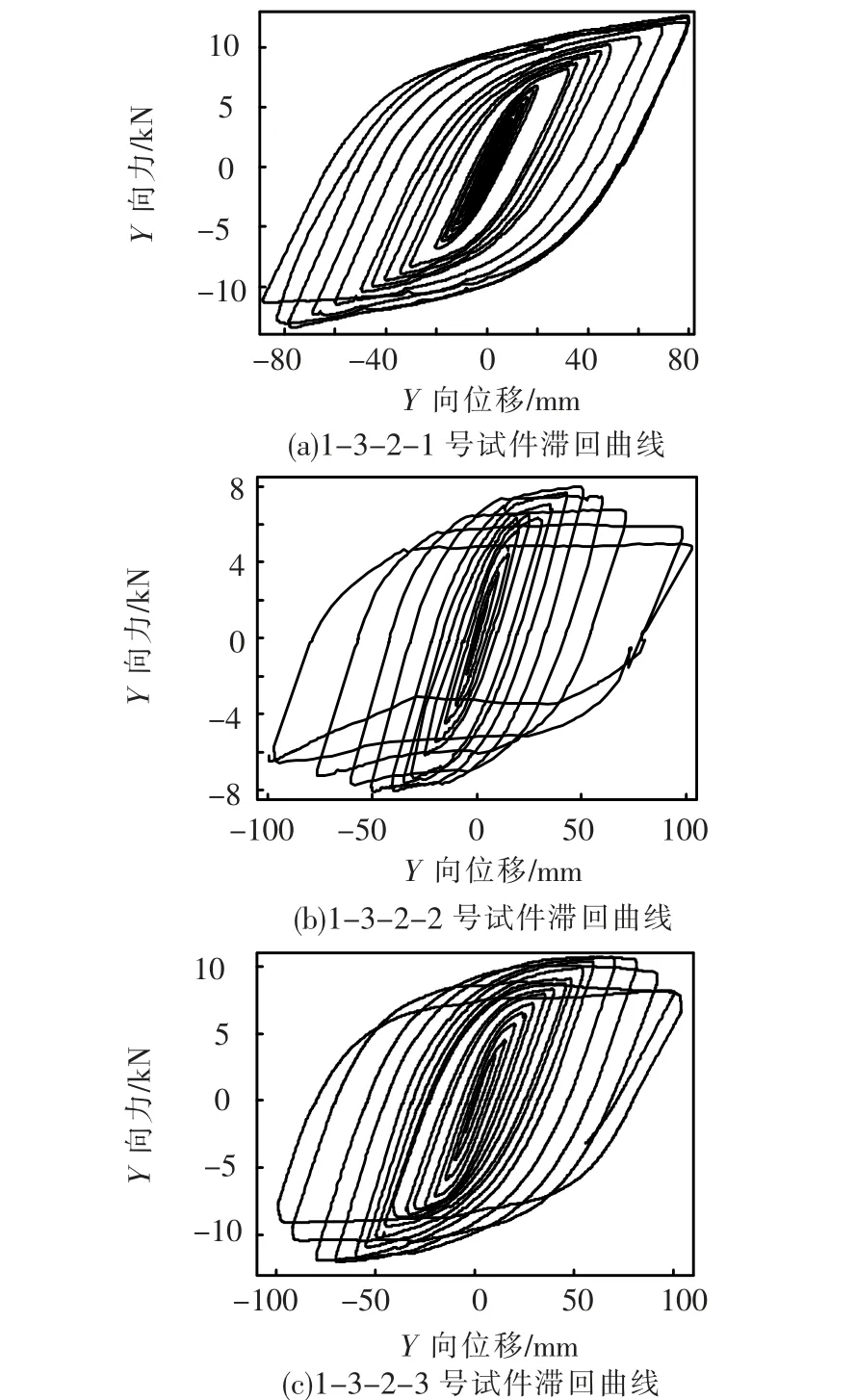
图4 试件滞回曲线

2.2 试验加载过程及现象

试验以编号3-1-3 的试件为例，试验获得的水平力与水平位移关系的滞回曲线随加载位移变化如图6 所示.该滞回曲线横坐标为圆钢管顶部的水平位移，纵坐标为圆钢管顶部水平力.本文仅给出测点2.2 的应变曲线.从试验过程及滞回曲线可以观察到如下规律:

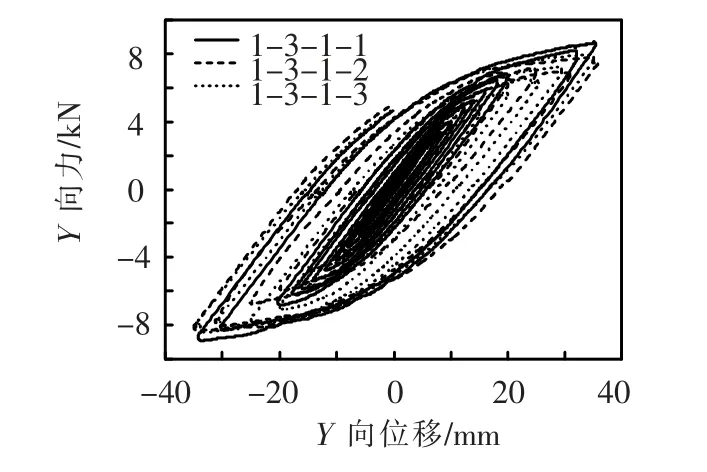
图5 试件滞回曲线对比

1)在弹性范围内循环加载时，试件滞回曲线的包络面积几乎为零，变形能为弹性应变能，几乎没有能量消耗.

2)循环加载过程中，荷载卸载到零时仍存在残余变形，对每一循环来说，残余变形随循环幅值的增加而增加.

3)在达到最大承载力之前，试件滞回性能很好;当试件达到最大承载力后，承载能力缓慢下降(加载位移为50 mm 左右)，表明此时试件具有很好的延性，但随着加载位移的继续增大(加载位移超过-60 mm 时)，试件的承载力下降速度加快，耗能能力迅速降低，表明试件的损伤已经很严重.

4)圆钢管试件在塑性发展已经很充分的情况下，仍然具有良好的滞回性能，如图6(h)所示，试件端部已经起鼓，但承载力仍呈上升趋势，表明试件的耗能能力仍然很强.由此认为圆钢管在地震荷载作用下也具有良好的耗能能力.

5)从试验过程中可以看到，当试件在某一方向屈曲后，继续施加荷载，一个方向施加的载荷将明显对其余两个方向产生影响.

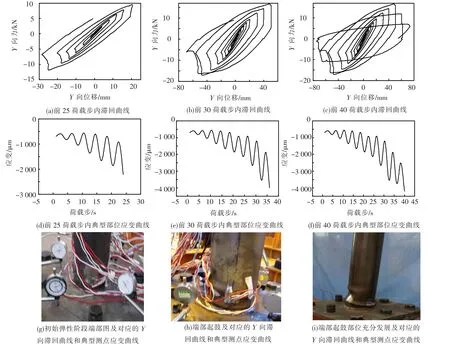
图6 试件3-1-3 底部起鼓发展及相应的Y 向滞回曲线和典型测点应变曲线

6)从试件典型部位的应变曲线图中(如图6)，可观察到在前25 个荷载步内，试件的应变随荷载增加而均匀增加，可推断出此时尚未达到最大应力，损伤累积不明显，而当30 个荷载步后，应变增加幅度明显变得剧烈，由试验过程中的观察亦可发现此时试件底部将起鼓，而应变在第40 个荷载步时迅速增加，表明此时试件将破坏.

2.3 试验结果分析

试验过程必然受到装置模拟的准确性以及外界因素的影响，以试件3-1-3 为例，本试验误差主要有3 个方面:

1)试验过程中，试件底部的钢箱将会产生刚体转动，对试验结果产生影响，如图7(b)所示.试验过程中，记录了图6(a)所示的4 个位移计的竖向位移(其位移随荷载变化曲线如图9(a)所示，限于篇幅，仅给出1、2 号测点的竖向曲线).以Y 方向为例，1、4中点位移可由二者竖向平均值得到，同理可得到2、3中点的位移.二者之间的关系如图7(b)所示，根据图示线性关系可求得由于钢箱转动而使试件顶端产生的位移.钢箱转动作用消除与未消除曲线对比如图9(b)所示.从处理结果可以看到，钢箱刚体转动造成最大的误差可达10%左右.

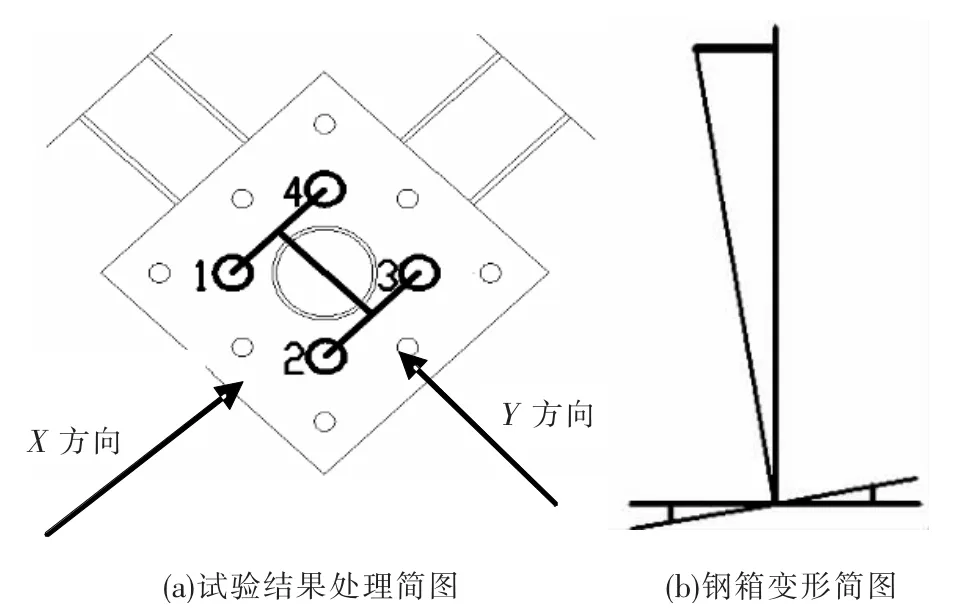
图7 钢箱转动处理简图

2)三维加载实验中一个不利的影响是双向推拉千斤顶的位移产生了几何非线性，如图8 所示.根据图8(b)中所示的几何关系:

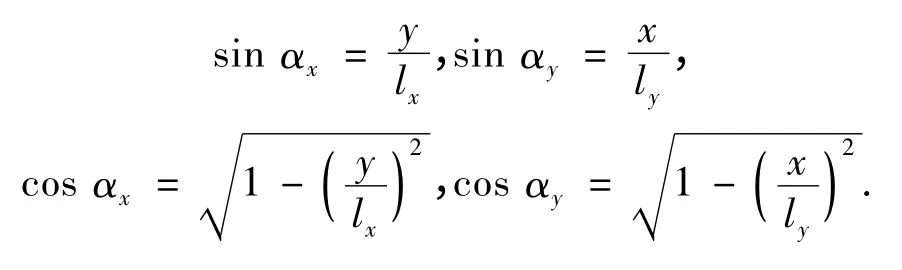
则试件在X 和Y 两方向的实际受力为

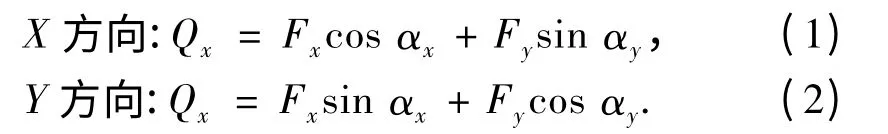
式中:Fx和Fy分别为推拉千斤顶所连接力传感器量测值，根据试件加载到最大位置时，相应的cos αx=0.997，sin αx=0.07，cos αy=0.998，sin αy=0.06，式(1)和式(2)中的正弦项可以忽略，余弦项认为等于1，因此实际受力近似等于力传感器测量值.

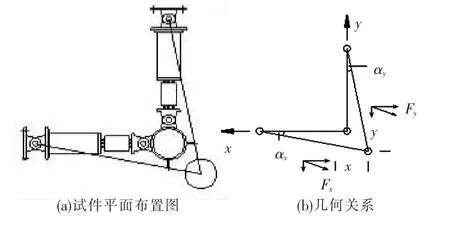
图8 双向水平位移的互相影响

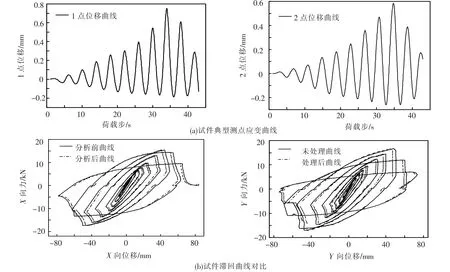
图9 试件3-1-3 典型测点应变曲线及滞回曲线对比

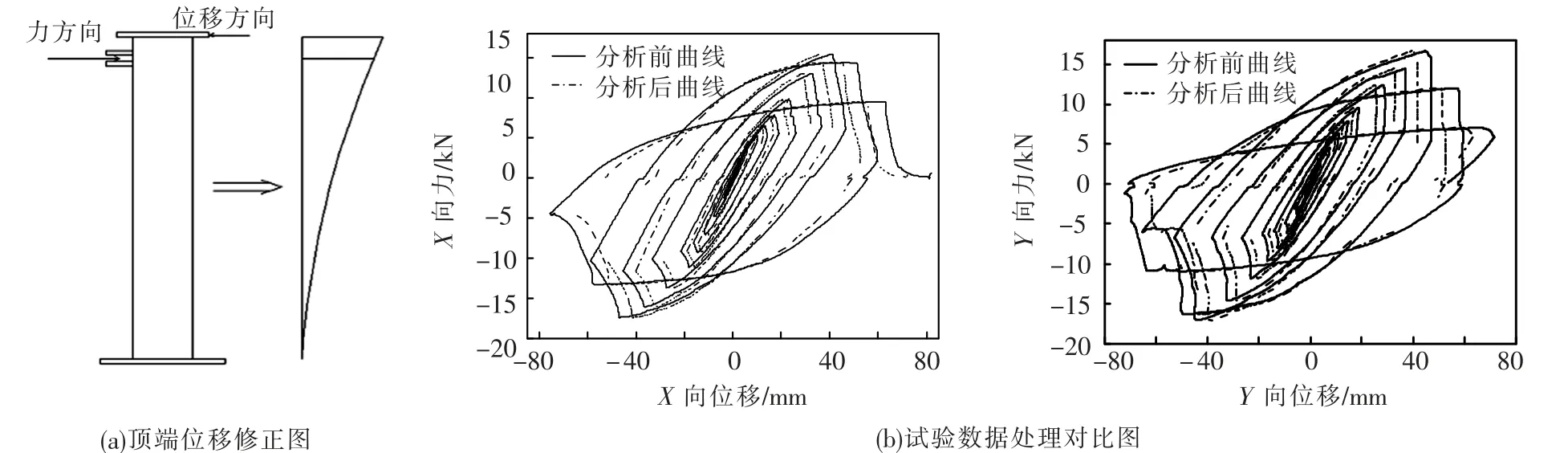
图10 试件3-1-3 顶端位移及试验处理对比图

3)试验过程中，试件加载部位的力传感器与 顶板的位移计不在同一高度，如图10(a)所示，在消除钢箱转动基础上，将顶端位移变换到力方向上.变换后曲线与原曲线(这里原曲线指消除钢箱影响后曲线)对比如图10(b)所示.

试验仍以编号3-1-3 的试件为例，试验获得的水平力与水平位移关系的滞回曲线经以上方法消除后最终如图11 所示.

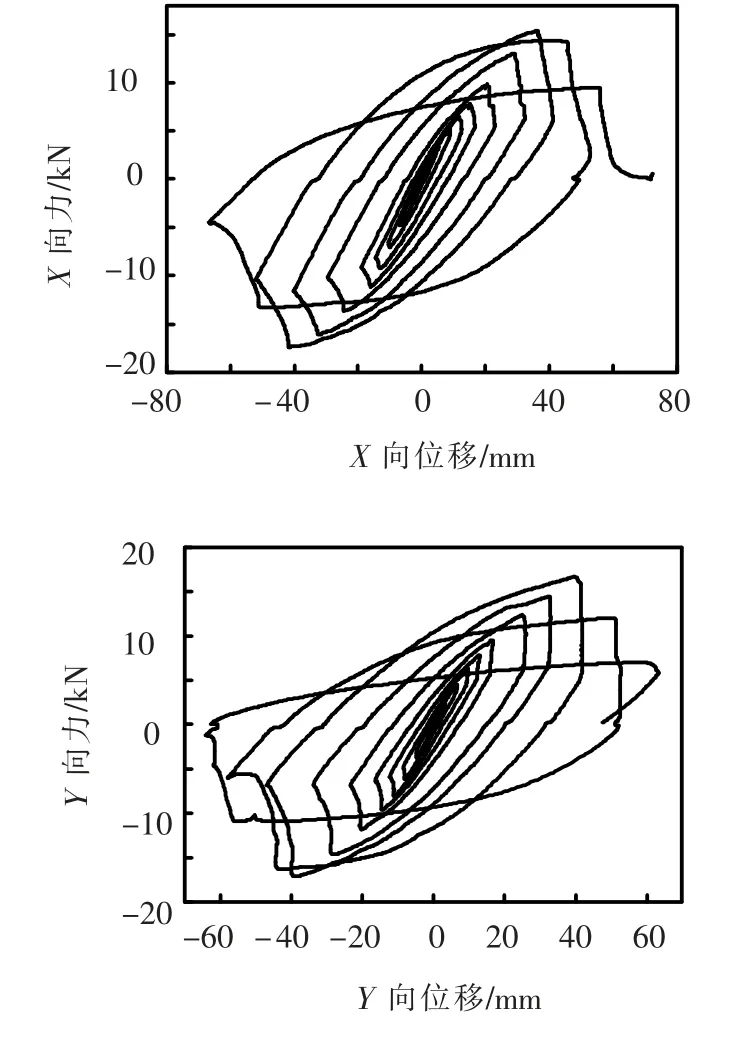
图11 试件3-1-3 滞回曲线

3 结 论

1)试验选取的设计参数对圆钢管构件具有代表性和覆盖面，试验结果离散性小，数据可靠.

2)设计了满足空间三向加载的试验装置，该装置可以适应不同长细比、不同空间加载方案的需要，操作方便，便于试件的安装拆卸.对比试验表明，装置具有良好的稳定性，能够满足试验精度要求.

3)试验数据处理过程中，剔除了各种不良因素的影响，如钢箱的刚体转动、力位移不在同一高度上造成的影响，均予以消除.

4)在试件起鼓之前，滞回曲线呈一直增强的状态，表明在起鼓之前试件的损伤累积并不明显，而当试件底部产生起鼓之后，从试验过程中可以看到试件的滞回能力明显变弱，表明试件起鼓后损伤累积在明显增加.

5)从试验过程中可以看到，圆钢管具有良好的滞回性能，在很大的位移作用情况下，仍能保持良好的耗能能力.

［1］SHEN Shizhao.Recent advances on the fundamental research of spatial structures in china［J］.Journal of the International Association for Shell and Spatial Structures，2006，47(2):93-100.

［2］XUE S D，WANG X S，CAO Z.Multi-dimensional excitation method for nonstationary random seismic analysis of spatial lattice shells［J］.International Journal of Space Structures，2004，19(3):129-136.

［3］FAN Feng，SHEN Shizhao.Study on the dynamic strength failure of reticulated domes under severe earthquakes［C］//International Association for Shell and Spatial Structures Symposium.Montpellier，France:［s.n.］，2004:140-141.

［4］KUMAGAI T，OGAWA T.Dynamic buckling behavior of single layer lattice domes subjected to horizontal step wake［J］.Journal of the International Association for Shell and Spatial Structures，2003，44(3):167-174.

［5］KATO S，MURATA M.Dynamic elasto-plastic buckling simulation system for single layer reticular domes with semi-rigid connections under multiple loadings［J］.International Journal of Space Structures，1997，12(3＆4):161-172.

［6］PARK Y J，ANG A H S.Mechanistic seismic damage model for reinforced concrete［J］.Journal of Structural Engineering，1985，111(4):722-739.

［7］PARK Y J，ANG A H S，WEN Y K.Seismic damage analysis of reinforced concrete building［J］.Journal of Structural Engineering，1985，111(4):740-757.

［8］沈祖炎，沈苏.高层钢结构考虑损伤累积及裂纹效应的抗震分析［J］.同济大学学报，2002，30(4):393-398.

［9］董宝，沈祖炎，孙飞飞.考虑损伤累积影响的钢柱空间滞回过程的仿真［J］.同济大学学报，1999，27(1):11-15.

［10］支旭东，范峰，沈世钊.材料损伤累积在网壳强震失效研究中的应用［J］.哈尔滨工业大学学报，2008，40(2):169-173.

［11］ZHI Xudong，FAN Feng，SHEN Shizhao.Failure mechanism of single-layer reticulated domes subjected to earthquakes［J］.Journal of the International Association for Shell and Spatial Structures，2007，48(1):29-44.