强震区桥台滑移变位特性及趋势研究

崔英明，刘家敏

(重庆市交通规划勘察设计院，重庆401121)

通过对汶川地震次生灾害的遥感解译、野外调查和初步分析发现，强震诱发了大量的崩塌滑坡［1－2］，尤其是陡峻基岩斜坡上崩塌滑坡密集发育。而地震造成的边坡地质灾害分布、发育有一重要特征是沿交通线分布，其中重灾区公路与铁路桥梁沿线较为典型［3］，其两侧桥台一般都建在两岸山体岸坡上，在地震波激励作用下，岩土体强度降低、孔隙水压力增大、裂隙增多以及由松散体产生的动土压力造成岸坡失稳，继而桥台与台后填土岸坡滑移，最终导致上部结构的破坏和倒塌。例如，国道213线都江堰—映秀公路是通往灾区映秀、汶川的南线通道，地震发生后该段道路桥梁均出现了比较严重的病害［4］，在 K1 020+592.03 寿江大桥的0#桥台，横向滑移导致第1跨30m的T梁横移，同时该跨T梁向映秀方向纵向滑移，并扭转下沉，面临整孔落梁危险，第1孔T梁左侧向桥台方向位移约50 cm，右侧向桥台方向位移约60 cm;在K1 011+611蒙子沟中桥，4#桥台台身向映秀侧推移约35 cm，4#桥台背墙破坏，全桥主梁横向向江心侧移动，左右两侧挡块均破坏;在映秀镇鱼子溪大桥1#大桥，桥台伸缩缝破坏，梁体向桥台方向纵向移动，与桥台连接的挡墙下沉约20 cm，盖梁挡块破坏，裂缝向下延伸至盖梁根部，主梁整体向岷江侧横向移动约10 cm。

在地震区桥台抗震设计中，传统方法是以作用于台背的地震土压力为依据［5－6］，采用拟静力法求得其稳定系数，但该方法的缺点是没有考虑桥台以及台后填土相互滑移作用，进而进行桥台变形控制，以致不能完全准确评定其动力稳定性［7］，同时根据汶川地震震后调查表明，桥台岸坡整体滑塌较少见，大多是局部滑移产生的永久性滑移。因此桥台岸坡抗震设计除强度、承载力外，位移控制［8］也是一个关键内容。

1 桥台地震位移估算模型

估算桥台震后位移一直是岩土工程抗震领域的核心问题，过大的台体位移不仅导致桥台本身的破坏，也给邻近的建筑物造成很大的影响。在地震作用下，桥台的位移模式将受多重因素影响，例如，台体几何形状、地震烈度、地震波特性、地基条件、台后填土坡脚等［9］。笔者在充分总结已有的桥台位移计算理论的基础上，建立滑移模式、转动模式以及滑移与转动耦合位移模式下的台体位移计算模型，并提出台体位移的简化计算方法，根据计算方法分析位移指数、滑移位移及位移分量百分比等指标在不同地震烈度下的变化情况。

1.1 滑移位移模型

桥台地震位移估算模型以Newmark滑块理论为基础［10］，地震作用下认为桥台存在一个临界加速度，当地震动加速度超过桥台临界加速度时，桥台将产生相对位移，当地震动速度与桥台速度相同时，相对位移停止，桥台震后位移为一系列滑移量的累积［11］，图1为Newmark滑块模型示意。

图1 Newmark滑块模型示意Fig.1 Newmark block model diagram

在给定的地震动加速度下，按照滑动模型计算桥台滑移位移时，首先应计算桥台的临界加速度，然后分别对加速度时程中大于临界加速度的部分及小于临界加速度的部分(直至台体与滑面无相对运动)进行2次积分，得到台体滑移累积位移。图2为桥台滑移位移模型受力示意图，当台体在地震作用下抗滑安全系数等于1时，即可求得桥台的滑动临界加速度。图中，台高为H，基底宽度为B，台背倾角为β，台体重量为W;PAE为台背地震土压力，按M－O公式计算(地震角按临界加速度系数计算)，合力作用点距台踵为h;基底土体内摩擦角为δb，台背摩擦角为δ，填土坡脚为i，根据受力平衡可知:

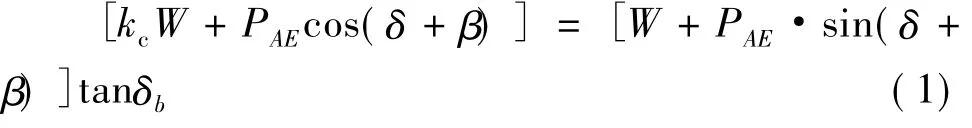
经数值迭代，可求得临界加速度系数kc。

图2 桥台滑移模型受力Fig.2 Forces of abutment sliding model

当桥台的临界滑移加速度和地震动加速度时程确定之后，就可计算有限滑动产生的累计变形，当地震动加速度在桥台处产生的惯性力方向与滑动面上静剪切力的水平投影方向相同时［12］，假如:当k(t)≤kc时，桥台不沿滑动面滑动;当k(t)＞kc时，桥台要沿滑动面滑动。滑动方向与静剪切力方向相同，桥台滑动加速度的水平分量ü(t)等于地震动加速度系数k(t)与临界加速度系数kc之差乘以重力加速度g［13］，即

当地震动加速度在桥台处产生的惯性力方向与滑动面上静剪切力的水平投影方向相反时，桥台不沿滑动面滑动。这样，在整个地震动加速度过程中，只有正半周或负半周才能使桥台沿滑动面滑动;在这些半周内桥台产生的惯性力方向与滑动面上剪切力水平投影方向相同。由于滑移加速度已由式(2)给出，因此每次滑动的水平位移Δi可按式(3)计算:

现在来考察在一个滑动半周内，滑动变形是如何发展的。如图3(a)，设在正半周内产生滑动。在t0－t1时段，k(t)≤kc不产生滑动;在t1－t2时段，将产生滑动，并且是滑动加速发展阶段;在t2－t3时段，虽然k(t)＜kc，但有初速度，滑动仍在发展，是滑动减速发展阶段，在t3时刻滑动速度成为0。从t0－t3滑动的速度和位移分别如图3(b)和3(c)。

图3 在半周内滑动的发展趋势Fig.3 Development of sliding trends during half period

1.2 转动位移模型

桥台震动位移估算模型以Zeng和Steedman提出的转动块理论为基础［14］，与Newmark滑块理论相似，Zeng和Steedman提出台体转动临界加速度的概念，对于任意给定的地震动加速度时程，如果地震动加速度超过转动临界加速度，台体发生转动，台体底面相对基底产生转角，一旦地震动加速度小于转动临界加速度，台体将产生抵抗其转动的恢复力和力矩，使台体转动速度开始减小，直至台体相对基底相对转速为0，台体总位移为一系列转角的累加［15］。图4为桥台转动位移模型受力示意图，当台体在地震作用下抗倾覆安全系数等于1时，即可求得桥台的转动临界加速度krg。图4中，台趾为桥台转动中心，并以其为坐标原点建立平面直角坐标系，质点转动半径为rc，角加速度为α，地震动加速度为αg，质心加速度分别为 (αc)y、(αc)x;PAE为台背地震土压力，按M－O公式计算。由受力平衡可知:

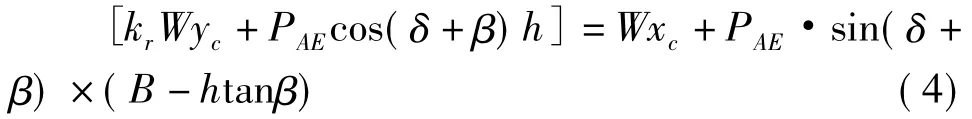
经数值迭代求解台体转动临界加速度系数kr。

图4 桥台转动模型受力Fig.4 Forces of abutment rotation model

1.3 滑移与转动耦合的位移模型

结合Newmark滑移模型及Zeng和Steedman转动模型，当地震动加速度既超过滑移临界加速度又超过转动临界加速度时，桥台将同时发生滑移和转动，位移模式为滑移与转动的耦合，台体位移为滑移位移与转动位移的总和。为简化计算，估算这种情况下的台体位移时，可按Newmark滑移模型及Zeng和Steedman转动模型分别计算滑移位移及台体转角，然后将二者计算结果进行叠加。

2 桥台地震位移计算方法及数据分析

为了便于计算，选择1971年San Fernando Pocoima Dam地面加速度时程，其峰值加速度为105.4 cm/s2，持续时间为41.70 s，地震动时程图如图5，地震动加速度在－1.0g与1.0g之间变动，y=kc·g为临界加速度线，其是确定桥台滑移起动与加速减速一条很重要的分界线。

图5 地震动加速度波形Fig.5 Waveform of seismatic dynamic acceleration

图6为一个滑动周期的滑动变化情况。在OS段，k(t)≤kc不产生滑动;在SR段，k(t)＞kc将产生滑动，并且是滑动加速发展阶段;在RP段，虽然k(t)＜kc，但有初速度，滑动仍在发展，是滑动减速发展阶段，在P点时刻滑动速度为0，滑动停止。

图6 一个周期内滑动时刻变化Fig.6 Slide times in a cycle

现计算S、R、P各点所处时刻。当在S点时，桥台刚开始发生滑移，此时k(t)＞kc，而根据P点处速度为0，即加速阶段加速度曲线所围面积与减速阶段加速度曲线所围面积代数和为0，得:

计算可得P点时刻xP。而桥台滑移位移应为SR和RP时段内台体滑移加速度的2次积分，即平动分量:

在整个地震期间，桥台滑动的水平位移Δ应是每次滑动水平位移Δi之和。因此:

式中:n为整个地震期间滑动的次数。

同理如果地震动加速度超过转动临界加速度kr，台体发生转动，台体底面相对基底产生转角，一旦地震动加速度小于转动临界加速度，台体将产生抵抗台体转动的恢复力和力矩，使台体转动速度开始减小，直至台体相对基底相对转速为0，即每一次转动分量为SR和RP时段内台体滑移加速度的2次积分，即:

在整个地震期间，桥台总转角为一系列转角的累加，即转动角度θ应是每次转动角度θi之和。因此:

笔者利用MIDAS/Civil对一桥台进行地震动力时程分析，地震波选用1971年San Fernando Pocoima Dam地面加速度时程，桥台台高为10m，顶面为边长为4m的正方形，底面桥台为8m的正方形，台背倾角为11°，台体容重为20 kN/m3，计算所得台背地震土压力为763 kN，基底土体内摩擦角为25°，台背摩擦角为5°，填土坡脚为8°，其桥台建模三维立体图如图7。

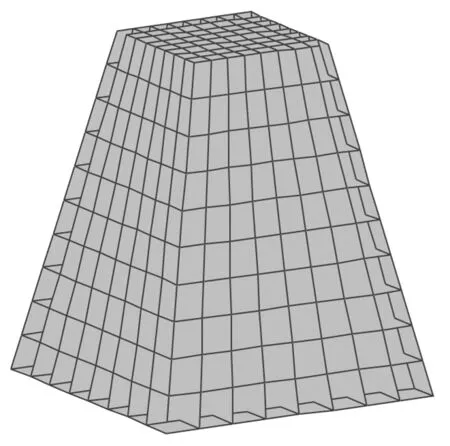
图7 桥台建模三维立体Fig.7 Three-dimensional abutment model

为了研究桥台实际位移特性，笔者认为桥台震动位移模式是滑动与绕台趾转动的耦合，即RBT位移模式，见图8。图中，台顶总位移为Δ1，平动分量为Δ，转动分量为 ΔR，Δ1=Δ+ΔR，台体转角为 θ。引入平动位移百分比Δ/Δ1、转动位移百分比ΔR/Δ1、位移指数Δ1/H(H为台高)3个指标对桥台震动位移特性及抗震性能进行综合评价。位移百分比反映了地震中台体的位移模式，平动位移百分比与桥台滑动位移成正比;转动位移百分比与桥台倾覆位移成正比;位移指数反映了台体震后的位移幅度，以量化方式衡量了桥台的抗震性能。

图8 桥台震动RBT位移模式Fig.8 RBT displacement mode of abutment vibration

通过数值模拟输入地震波，得出桥台的变形图以及位移等值线图，分别如图9～图11。

图9 桥台变形三维立体Fig.9 Three-dimensional displacement of abutment model

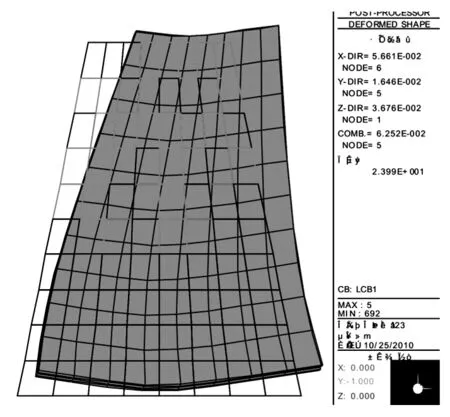
图10 桥台变位侧视Fig.10 Side view of displacement of abutment

图11 桥台变形位移等值线Fig.11 Displacement contour of abutment

根据数值分析结果，考虑地震动加速度大于临界加速度的滑动加速阶段和滑动减速阶段，根据以上公式分别求出在不同的地震动加速度情况下的平动分量 Δ、转动分量 ΔR、总位移 Δ1、位移指数Δ1/H、平动百分比 Δ/Δ1、转动百分比 ΔR/Δ1，如表1。

表1 各滑块岩体力学参数Tab.1 Mechanical parameters of slide rocks

图12～图14分别列出了位移指数、滑移指数及位移分量百分比在不同地震加速度下的变化情况。图12中，当地震动加速度为0.2g时，台体几乎不发生位移，位移指数接近0;当地震动加速度为0.3g时，位移指数仅为0.04%;当地震动加速度为0.4g时，位移指数为0.07%，近似达到0.3g时的2倍;当地震动加速度增至0.7g时，位移指数为0.32%，近似达到0.4g时的5倍;当地震动加速度达到0.8g、0.9g时，台体位移大大增大，位移指数分别达到 0.55%、0.66%。

图12 位移指数随地震加速度变化曲线Fig.12 Relationship between displacement index and earthquake acceleration

图13 中，当地震动加速度为 0.2g、0.3g、0.4g、0.5g时，桥台滑移位移几乎为0;当地震动加速度超过0.5g后，桥台滑移量开始缓慢增加，到0.6g时，滑移位移增至2.31 mm;当地震动加速度达到0.8g、0.9g时，桥台滑移位移增幅程度明显加深，滑移量分别达到10.42 mm、18.57 mm。

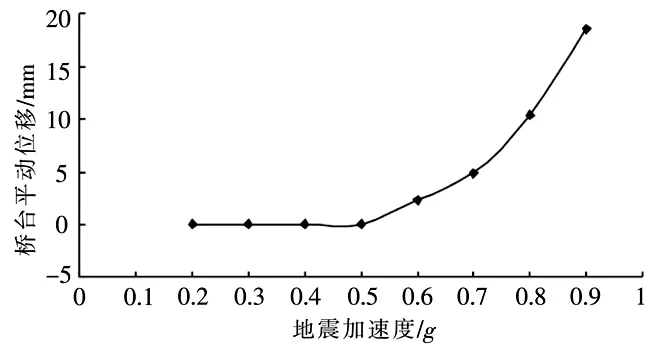
图13 桥台平动位移随地震加速度变化曲线Fig.13 Relationship between abutment translationaldisplacement and seismic acceleration

从图14中可看出转动分量在台顶总位移中占较大比例，转动分量百分比随地震系数的增大而减小，平动分量百分比随地震系数的增大而增大。当地震动加速度为 0.3g、0.4g、0.5g时，桥台只发生转动，转动分量百分比为100%;当地震动加速度大于0.5g时，转动分量百分比逐渐减小，平动分量百分比逐渐增加;当地震动加速度为0.6g～0.8g之间时，转动、平动分量百分比随地震系数的变化而变化很小，转动分量百分比约是平动分量百分比的5.67倍;当地震动加速度大于0.8g时，平动分量百分比又开始逐渐增大，到0.9g时转动分量百分比约为平动分量的2.57倍。

图14 平动分量和转动分量随地震加速度变化曲线Fig.14 Variation curve of translational component and rotational component with the change of earthquake acceleration

3 结论

笔者在充分总结已有的桥台位移计算理论的基础上，以Newmark滑块及Zeng和Steedman转动块理论为基础，建立滑移模式、转动模式以及滑移与转动耦合位移模式下的台体位移计算模型，并提出了台体位移的简化计算方法，根据计算方法分析位移指数、滑移位移及位移分量百分比在不同地震烈度下的变化情况，得出以下几点结论:

1)当地震烈度为7度及以下时，台顶变位微小，可近似忽略;当地震烈度为8度时，台顶变位略呈上升趋势，但其增幅与7度区相比仍不明显;当地震烈度为9度及以上时，台顶变位迅速增大，增幅程度也随地震烈度的升高而大大加快。

2)当地震烈度小于8度时，桥台几乎不发生滑移位移;当地震烈度达到8度时，台体才开始出现滑移位移，当地震烈度为9度及以上时，台体滑移量增幅程度随地震烈度的增加而愈加显著。

3)台体位移模式受地震烈度影响显著，随着地震系数的增大，台体逐渐由转动的位移模式向转动+滑动的位移模式转变。当地震烈度小于8度时，台体几乎不发生滑动，台体位移几乎全部由转动产生，位移模式为转动;当地震烈度为8～9度之间时，平动分量逐渐增加，转动分量逐渐降低，位移模式为转动与平动的耦合;当地震烈度大于9度时，平动分量的变化逐渐由保持定值到呈上升趋势，位移模式仍为转动与平动的耦合，但台体滑移位移占总位移的百分比大大增加。

［1］李鸿晶，陆鸣，温增平，等.汶川地震桥梁震害的特征［J］.南京工业大学学报，2009，31(1):24 －29.

［2］庄建琦，崔鹏，葛永刚.5.12汶川地震崩塌滑坡分布特征及影响因子评价:以都江堰至汶川公路沿线为例［J］.地质科技情报，2009，28(2):16 －22.

［3］雷涛，李碧雄，曹鹏杰，等.汶川地震近断层附近桥梁震害浅析［J］.重庆交通大学学报:自然科学版，2010，29(3):358－496.

［4］张鹏，陈新民，王旭东.近断层地震动与汶川地震灾区滑坡破坏特征分析［J］.南京工业大学学报，2009，31(1):55－59.

［5］宋胜武.汶川大地震工程震害调查分析与研究［M］.北京:科学出版社，2009.

［6］何度心.桥台抗震设计的理论与方法［J］.世界地震工程，1991(3):1－15.

［7］李海波，肖克强，刘亚群.地震荷载作用下顺层岩质边坡安全系数分析［J］.岩石力学与工程学报，2007，26(12):2385－2394.

［8］吕艳，齐怀恩.桥台抗滑移的稳定可靠度［J］.公路，2002(1):38－39.

［9］李德武，梁波，韩文峰.桥台岸坡滑移地震稳定性分析［J］.岩石力学与工程学报，2003(Z2):2813－2818.

［10］Robert H，Dinand A，Gerard A M，et al.Influence of earthquakes on the stability of slopes［J］.Engineering Geology，2007，91(1):4－15.

［11］吴世明.土动力学［M］.北京:中国建筑工业出版社，2000.

［12］祁生文，伍法权，严福章，等.岩质边坡动力反应分析［M］.北京:科学出版社，2007.

［13］Scholl R E，King JL.Strong ground motion simulation and earthquake engineering applications［M］.California:USA Earthquake Engineering Research Institute，1985.

［14］许年春，石维力，石东虹.结构动力有限元程序设计地震作用下边坡动力系数有限元分析［J］.地下空间与工程学报，2008，4(6):1006 －1010.

［15］Conte J P，Pister K S，Mahin S A.Influence of the earthquake ground motion process and structural properties on response characteristics of simple structures［R］.Berkeley:Earthquake Engineering Research Center，1990.

［16］董志高，吴继敏，王文远，等.地震作用崩塌堆积体边坡稳定性分析［J］.水利水电科技进展，2006，26(5):37－40.