钢桁梁梁端横向伸缩对轨道几何形位的影响
全顺喜,王 平,陈 嵘
(西南交通大学高速铁路线路工程教育部重点实验室,四川成都610031)
随着我国高速铁路的建设和发展,无缝线路在各种形式的桥梁上得到了广泛的应用。当无缝线路铺设在梁宽跨度较大的钢桁梁上时,一方面由于钢桁梁的最大日温差相对较大;另一方面由于实际条件的限制,一般在钢桁梁的两边各设计一个支座,且在横向一端固定,另一端可以自由活动。这使得钢桁梁在最大日温差作用下将发生比较大的横向伸缩位移,即钢桁梁的两端相对路基或其它梁体会产生梁端的相对伸缩,这会对轨道的几何形位产生一定的影响。
以往对线-桥纵向相互作用曾进行了广泛而深入的研究,其计算方法逐渐由解析法发展到有限元法,计算模型由只考虑一根钢轨的平面模型发展到考虑多线的空间计算模型[1-5]。但对于梁端横向出现相对位移后,梁轨横向相互作用目前研究得甚少,笔者采用有限单元法建立线-桥横向分析模型,对钢桁梁梁端横向伸缩对有砟轨道几何形位的影响以及在梁端横向伸缩时影响轨道几何形位变化的各个因素进行分析。
1 计算模型的建立
与常规的梁轨纵向相互作用相比,梁端相对伸缩引起的梁轨横向相互作用具有不同的结构特点:对于有砟轨道线路,梁端产生横向相对伸缩后,桥梁首先通过道床带动轨枕发生横向位移,然后轨枕通过扣件带动钢轨发生横向位移,并且轨枕和钢轨的横向位移,在横向与离桥梁横向固定支座的距离有关;在纵向与离梁端的距离有关。针对此种情况,笔者在以往模型的基础上,按照轨道实际布置,将轨枕纳入线桥系统,应用有限元软件建立了有砟轨道“线-枕-桥”横向相互作用的三维分析模型,如图1。

图1 梁轨横向相互作用的分析模型Fig.1 Analysis model of lateral interaction between girder and rail
本模型以3种不同的单元模拟出包含钢轨、扣件、轨枕、道床和桥梁为一体的“线-枕-桥”横向相互作用的分析模型。以普通的平面梁单元模拟钢轨和轨枕,且考虑了剪切变形的影响;分别利用弹簧单元模拟钢轨与轨枕的扣件连接、轨枕与桥面的道床连接,能考虑扣件和道床的横向弹性系数、纵向弹性系数以及扣件的扭转弹性系数;由于不考虑桥梁的弯曲,以壳单元模拟桥梁的横向变形。
2 梁端横向相对伸缩对轨道几何形位的影响
2.1 计算参数
双线特大桥的钢桁梁长865.80m,一端与8跨简支梁衔接,另一端与路基衔接。笔者以钢桁梁与路基衔接端为研究对象,其中钢桁梁两侧的横向固定支座与活动支座的距离为18m,线间距为4.4m,两线轨道对称布置在钢桁梁的中间。钢桁梁的弹性模量E=2.06×105MPa,热膨胀系数 α =1.18×10-5,梁温度差按钢梁日温差取值,为 ±25 ℃[6]。
线路条件为:60 kg/m无缝钢轨,轨距为1.435m,Ⅲ型混凝土枕,轨枕间距为0.6m。当道床与轨枕间的纵向相对位移u≤2 mm时,道床纵向阻力r=7.5ukN/(m·轨),当u>2 mm 时,r=15 kN/(m·轨);道床横向阻力q(N/cm)与位移f(cm)的非线性关系为:q=25.11 -1 012.87f+1 014.1f3/4;当扣件与钢轨间的纵向相对位移u≤2 mm时,扣件纵向阻力r=12ukN/(m·轨),当u>2 mm时,r=24 kN/(m·轨)[6]。取单个扣件的横向弹性系数为5.0×104N/cm,扭转弹性系数 2.07×104N·cm/rad[6]。
2.2 钢桁梁横向伸缩后轨道几何形位的变化
钢桁梁在日温差作用下相对于路基会发生横向伸缩,钢桁梁的横向伸缩会带动道床、轨枕和钢轨产生横向位移,使线路产生方向不平顺。取以上参数,钢桁梁与路基衔接处轨道的横向位移如图2,轨道的方向不平顺变化率如图3。其中,离钢桁梁横向固定支座较近的为第1线,较远的为第2线,钢桁梁与路基衔接处的横向坐标为72m。由图可见,在钢桁梁横向伸缩后将会使轨道产生较大的横向位移,当钢桁梁两侧横向固定支座与活动支座的距离为18m,线间距为4.4m时,第2线轨道的最大横向位移达到了3.4 mm,且其大小随着轨道离横向固定支座距离的增大而增大,第2线轨道的横向位移比第1线轨道大1.3 mm;同一线两钢轨所产生的横向位移相等,即钢桁梁横向伸缩对线路的轨距没有影响,这是因为同一线的两根钢轨同在一根轨枕上,钢桁梁横向伸缩时主要通过道床带动包括轨枕和钢轨在内的轨道框架一起发生横向位移;轨道的横向位移并不是突然产生的,而是在钢桁梁与路基衔接处有一个约为8m过渡区,从第1、第2线轨道的方向变化率可以看出,在钢桁梁与路基衔接处轨道的方向变化最快,其中在离钢桁梁横向固定支座较远的第2线轨道的方向变化率已超过1‰,为1.67‰。

图2 钢桁梁与路基衔接处轨道的横向位移Fig.2 Lateral displacement of track at the connection section of the steel truss girder and subgrade

图3 钢桁梁与路基衔接处轨道的方向变化率Fig.3 Change rate of track alignment at the connection section of the steel truss girder and subgrade
2.3 轨道几何形位变化的影响因素分析
从以上分析可知,钢桁梁在日温差作用下带动轨道框架相对路基产生较大的横向位移,且这一横向位移在桥梁与路基的衔接处存在一个过渡区。为了保证线路的高平顺性,应使轨道在桥梁与路基衔接处的横向位移、轨道变形后的方向变化率较小。下面对在钢桁梁产生横向伸缩后影响轨道几何形位变化的各个因素进行分析。
2.3.1 扣件、道床横向阻力对轨道几何形位变化的影响
扣件横向阻力分别取正常时的 0.2,0.5,1,2倍,其它参数不变,第2线钢桁梁与路基衔接处轨道的横向位移、轨道的方向不平顺变化率如图4、图5。由图可以看出,扣件横向阻力对轨道的最大横向位移影响不大,但随着扣件横向阻力的增大,轨道变形过渡区的长度逐渐变短,变形后方向不平顺变化率逐渐增大,当扣件横向阻力大于正常值5.0×104N/cm后,对其影响不明显。

图4 不同扣件横向阻力,轨道的横向位移Fg.4 Lateral displacement of track under different fastening lateral resistance

图5 不同扣件横向阻力,轨道的方向变化率Fg.5 Change rate of track alignment under different fastening lateral resistance
道床横向阻力分别取正常时的 0.2,0.5,1,2倍,其它参数不变,第2线钢桁梁与路基衔接处轨道的最大横向位移、最大方向不平顺变化率如表1。由1表可知,与扣件横向阻力对轨道几何形位变化的影响一致,道床横向阻力对轨道的最大横向位移影响不大,但随着道床横向阻力的增大,轨道变形过渡区的长度逐渐变短,变形后方向不平顺变化率逐渐增大,当道床横向阻力大于正常值后,对其影响不明显。

表1 不同道床阻力轨道最大横向位移和方向变化率Tab.1 Change rate and maximum lateral displacement of track alignment under different ballast lateral resistance
2.3.2 桥梁厚度对轨道几何形位变化的影响
桥梁厚度分别取0.5,0.06m,其它参数不变,第2线钢桁梁与路基衔接处轨道的横向位移如图6。由图6可知,不同的桥梁厚度,轨道所发生的横向变形几乎一致。这说明,由于钢桁梁较长,其在竖截面的面积以及材料的弹性模量较大,在其发生横向伸缩后,轨道框架的横向抗弯刚度对其影响很小,故桥梁厚度的取值对计算结果影响很小。

图6 不同桥梁厚度轨道的横向位移Fg.4 Lateral displacement of track under different thickness of the bridge
2.3.3 固定支座与线路中线间的距离对轨道几何形位变化的影响
其它参数不变,当钢桁架桥横向固定支座与活动支座的距离分别为9,12,15,18m,即固定支座与线路中线的距离分别为6.7,8.2,9.7 和11.2m 时,钢桁梁与路基衔接处轨道的横向位移、轨道的方向不平顺变化率以及钢轨最大横向位移、方向变化率与固定支座到线路中线间距离的关系曲线分别如图7~图9。从图中可以看出,轨道的横向位移、方向不平顺变化率随着横向固定支座到线路中线的距离的增加而增加,当横向固定支座到线路中线的距离控制在6.7m以内,即横向固定支座与活动支座控制在9m时,衔接处轨道的方向不平顺变化率小于1‰,此时轨道的最大横向位移约为2 mm。
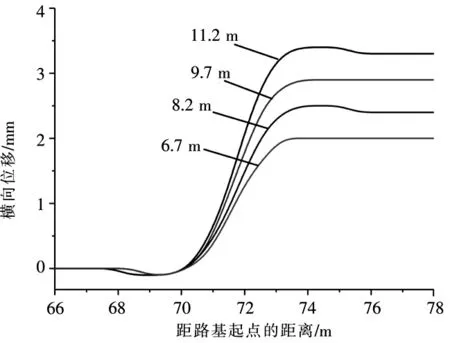
图7 固定支座与线路中线间的距离不同,轨道的横向位移Fig.7 Lateral displacement of track under different distance from lateral fixed support of steel truss girder to central line of the route

图8 固定支座与线路中线间的距离不同,轨道的方向变化率Fig.8 Change rate of track alignment under different distance from lateral fixed support of steel truss girder to central line of the route

图9 钢轨最大横向位移、方向变化率与固定支座到线路中线间距离的关系Fig.9 Relationship between track maximum lateral displacement and change rate of track alignment and distance from lateral fixed support of steel truss girder to central line of the route
3 结论
通过对钢桁梁梁端横向相对路基伸缩时有砟轨道几何形位的变化及其影响因素的分析,可以得出以下结论:
1)钢桁梁在日温差作用下,相对路基发生横向伸缩后将会使有砟轨道产生较大的横向位移和方向变化率。当钢桁梁两侧横向固定支座与活动支座的距离为18m,线间距为4.4m时,第2线轨道的最大横向位移为3.4 mm,最大方向变化率为1.67‰。
2)钢桁梁横向伸缩对有砟轨道线路的轨距没有影响,钢桁梁横向伸缩时通过道床带动包括轨枕和钢轨在内的轨道框架一起发生横向位移。
3)梁端伸缩时,道床和扣件横向阻力对轨道横向位移的影响很小,但随着道床、扣件横向阻力的增大,轨道的方向不平顺变化率逐渐增大,当增大到正常值之后,基本保持不变。表明为增强梁端横向发生相对伸缩处轨道的稳定性时,可以通过采取增加道床和扣件横向阻力的措施。
4)轨道的横向位移、方向不平顺变化率随着钢桁梁横向固定支座和线路中线间距离的增大而增大,当横向固定支座到线路中线的距离控制在6.7m以内,轨道的方向不平顺变化率小于1‰,轨道的最大横向位移约为2 mm。
[1]FrybaL.Starting and breaking borces in railroad bridges[J].Stavebnicky Casopis,1979,27(12):865 -894.
[2]Arya A S,Agrawal S R.Dispersion of tractive and braking forces in railway bridges theoretical analysis[J].Rail International,1982,13(4):12-25.
[3]卢耀荣.无缝线路研究与应用[M].北京:中国铁道出版社,2004.
[4]阴存欣.铁路桥梁纵向附加力静动力非线性分析与仿真研究[D].北京:铁道部科学研究院,2000.
[5]徐庆元.高速铁路桥上无缝线路纵向附加力三维有限元静力与动力分析研究[D].长沙:中南大学,2005.
[6]雷晓燕,圣小珍.现代轨道理论研究[M].北京:中国铁道出版社,2006.

