有效市场就没有收益率的均值回复吗?＊——基于理性资产定价模型的研究

王美今,陈 锐

有效市场就没有收益率的均值回复吗?＊
——基于理性资产定价模型的研究

王美今,陈 锐

通过构造理性定价模型,利用宏观经济状态的变化来反映市场风险,证明在有效市场中,股票收益率也能呈现出均值回复特征,其原因除了小样本的偏差外,还可能是理性经济人的风险厌恶和平滑消费意愿的结果。因此,均值回复现象不能作为拒绝我国股票市场弱势有效的证据。

均值回复;市场有效;理性预期;状态转移;方差率

一、问题的提出与文献回顾

有效市场理论在现代金融学中占据着主导地位。它认为证券价格总是可以充分体现可获得的信息的变化,信息的变化会在证券价格上得到及时准确的反映,信息是证券价格的惟一变量;在一个风险中性投资者组成的竞争市场中,证券价格是不可预测的。著名的随机漫步理论与早期的许多实证检验都支持股票价格不可预测的结论。有效市场理论成为金融学的绝大多数研究领域、尤其是证券分析理论的基础。

但是近二三十年来,有效市场理论在理论和实证检验两方面同时受到了挑战,股票价格变动具有一定的可预测性,其中长期收益比短期收益更容易预测。均值回复就是长期趋势可预测理论与方法的主要代表。所谓均值回复(Mean Reversion),是指股票价格无论高于或低于价值均值都会以很高的概率向价值均值回复的趋势。均值回复是股票价格可预测理论的一个突破性进展,也是对传统随机漫步理论的一个最大的挑战。

关于均值回复理论,在国外已有很多文献。法玛和弗兰慈(Fama和French,1988)、波特巴和萨莫斯(Poterba和Summers,1988)对美国纽约股票市场进行了实证研究,首次得出了股票收益长期呈均值回复的结论。随后对其他市场的大量研究也发现均值回复的现象①这些市场包括美国股票的其他市场(Gropp,2004;Nam等,2002)、其他发达国家或地区的股票市场(Balvers等, 2000)和东南亚国家或地区的股票市场(Malliaropulos和Priestley,1999)。,与此同时,也有不少学者找到反对均值回复存在的证据②这些证据包括：美国股票市场数据的小样本偏差(Lo和MacKinlay,1989;Richardson和Stock,1989;Richardson, 1993)和样本时期选择偏差(Jegadeesh,1991;Kim等,1991;McQueen,1992;Gangopadhyay和Reinganum,1996)以及新兴市场并不明显的均值回复的特征(Chaudhuri和Wu,2003)。。对均值回复现象的理论解释同样存在较大分歧：Poterba和Summers(1988)将股价的均值回复归结为部分投资者对特定市场信息过于乐观或悲观的估计而引起的过度反应和反应不足,即市场非有效;Fama和French(1988)也认为股价的均值回复现象是市场的非理性行为导致股价长期偏离其内在价值的结果,但同时提出时变理性预期(Time-Varying Rational Expectations)的解释,认为股票价格对其内在价值的偏离增加了股价的波动性,投资者因而要求获得额外的风险补偿,而增加了的风险补偿又会使股价向均值回复。也就是说投资者会根据股票价格的不同波动程度调整其预期收益率,均值回复源自投资者的理性定价调整。可见,在Fama和French看来,市场理性预期下的定价调整也可能产生均值回复现象,均值回复现象不是市场非理性的必然结果。

国内关于均值回复的研究不多。宋玉臣和寇俊生(2005)利用自相关检验和方差比率非参数自抽样测量方法,对从指数发布日起至2004年12月的沪深股市A、B股市场4个指数的月收益率进行实证检验,发现上证综合指数具有显著的均值回复特征;赵振全等(2005)利用ANSTGARCH模型对1996年1月至2003年12月沪深股市日收益率序列进行检验,发现经过风险调整的收益率序列仍具有非对称均值回复特征,负收益率的均值回复速度和幅度都明显大于正收益率的均值回复速度和幅度,并由此拒绝Fama的时变理性预期假设,断定均值回复是市场投资主体的非理性行为所导致的股票价格的系统偏差所致。

现在的问题是,拒绝了Fama提出的时变理性预期模型能说明均值回复现象就是市场非理性行为所致吗?Poterba和Summers(1988)认为,股票收益序列相关特征是否能成为拒绝市场有效的依据,需要构造能产生均值回复现象的理论模型(如非理性模型中的噪声交易者模型或具有时变预期收益率的理性预期模型)并进行实证检验,这需要借助股票收益率以外的其他数据信息,以反映股票内在价值以及噪声交易行为或时变的预期收益率。因此仅从中国股票收益率数据中得出均值回复的结论就推断市场非有效,有失偏颇,因为还可能存在其他未能被拒绝的、能产生均值回复现象的理性预期模型。

本文根据Poterba和Summers(1988)的思想,构建了一个时变理性预期模型,利用宏观经济状态的波动(宏观消费信息)来反映时变的预期收益率;使用方差率统计量来衡量收益率序列的均值回复特征,对理性预期模型下收益率序列是否真正存在均值回复现象进行检验,并判断上证收益率的均衡回复现象是否可由该理性模型产生。结果表明,基于消费的时变理性预期模型能解释上证指数的实际收益率的均值回复现象,均值回复现象并不能作为市场非有效的证据。

二、理性预期模型设定

本文采用的理性预期模型为常相对风险效用函数的卢卡斯纯交换经济模型(Lucas,1978)①在研究股票收益率的均值、方差、相关系数等各种特征的理性预期模型的文献中,具有常相对风险规避系数的纯交换经济模型是最常用的。本文主要是考察在给定消费增长的一个较为准确的马尔科夫状态转移过程下,理性预期模型的股票收益率是否能产生与实际观察到的相吻合的均值回复特征。考虑纯交换经济模型下消费效用函数的其他形式或者是生产经济模型也未尝不可。。该模型假设存在大量可无限存活的同质经济人和固定数量资产,这些资产生产同质的不可储存的消费品,消费品的数量是外生的。每份资产的权益完全可分,且在一个完全竞争的证券市场上交易。那么经济人优化问题的一阶条件表示为：

其中Pt为资产以消费品计量的实际价格;U′(C)为经济人消费的边际效用;β为时间贴现率,0＜β＜1;Dt+1为资产的支付或红利;Et表示基于时期t的信息的条件期望。

在均衡时该模型的消费等于红利,(1)式转化为：

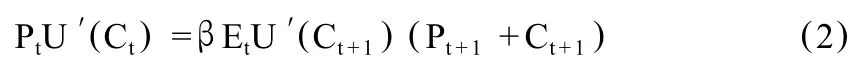
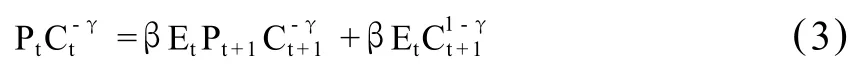
三、消费增长的状态转移模型的构造

利用宏观经济状态的波动(宏观消费信息)来反映时变预期收益率的思想由来已久(Kandel和Stambaugh,1990;1991)。班塞尔和亚龙(Bansal和Yaron,2004)、莱托(Lettau等,2008)的研究均表明,20世纪90年代以来,美国股票市场收益率的下降源于其宏观消费波动的降低。因为在经济高涨或稳定时期,股票收益率通常较低;而在经济低迷或波动期,人们通常要求较高的股票收益率。在股票收益率的预测文献中,学者们也认为成功的预测变量通常能反映宏观经济状态的变化(Rapach等,2010)。本文采用人均消费增长来反映预期收益率的变化,并用状态转移模型(Hamilton,1989)对消费增长的均值和标准差建模,该过程对于刻画宏观变量的运动具有特殊的优势,也得到广泛的应用(Ki m和Nelson,1999; McConnell和Perez-Quiros,2000;Lettau等,2008)。

(一)数据来源

根据上述结论,首先利用实际的统计数据拟合出适当的消费增长过程;其中总消费数据来源于CCER中国宏观经济数据库的“社会消费品零售总额”和“市社会消费品零售总额”;人口数据来源于中经网的“年底总人口数”和“年底城镇总人口数”,并将人口年度增长率按几何平均法转化成月度增长率来计算月度总人口数;消费价格指数根据“居民消费价格指数”构造,即选取中经网2001年1月到12月的环比数据和CCER中国宏观经济数据库1991年1月到2008年12月的同比数据,并由此计算以2001年1月为基期的定基比消费价格指数;由此可计算实际人均月度消费量,并采用对数相加形式的调整因子对其进行季节调整(Findley等,1998)。后文使用的上证指数收益率的数据来源于CCER证券市场指数数据库并经通货膨胀率的调整;通货膨胀率数据由消费价格指数计算而来。

表1给出了全国人均消费增长数据的描述性统计量,还列出了以相乘形式的调整因子进行调整后的数据的相关统计量,可见不同的调整方法对结果的影响不大。同时考虑到中国股票市场的有限参与问题①经济中并非所有经济人参与股权交易,此时定价模型中使用社会人均消费可能不妥。,表中还列出了全国城镇人均消费增长的相关统计量,其数据特征与全国人均消费增长的数据相似,后文的研究表明,这两组数据都支持相同的状态转移模型。

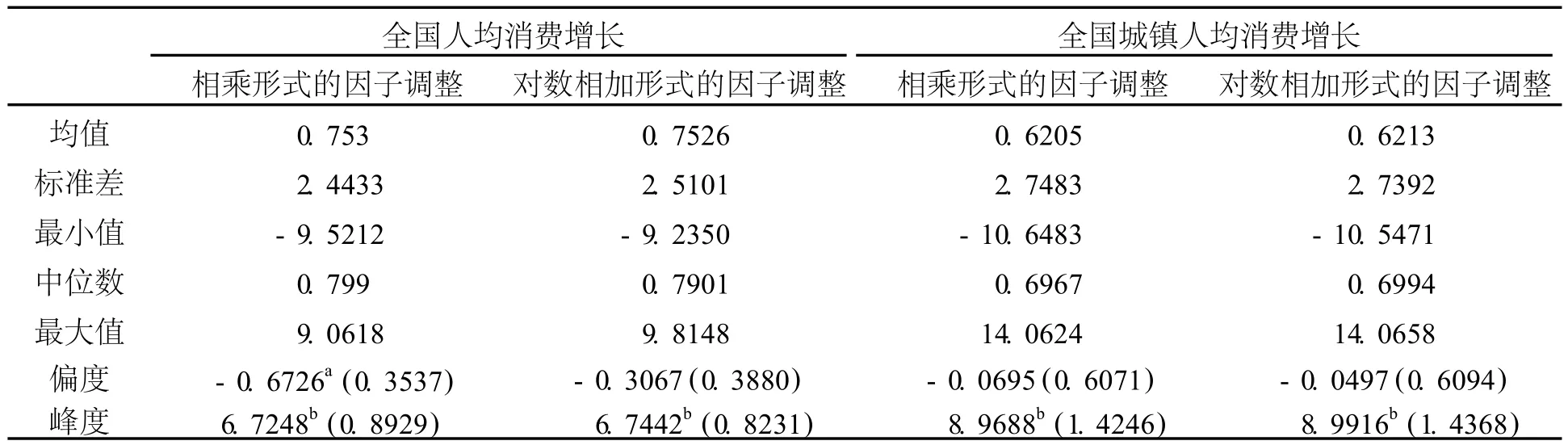
表1 消费增长的描述性统计量

从表1可见,相对于正态分布,数据呈现出非对称性和厚尾特征。其中非对称性由偏度系数来衡量,厚尾特征由峰度系数来衡量。不同数据和不同月度调整方法计算的偏度系数均为负,其中以相乘形式的因子进行调整后的全国人均消费增长数据在5%的水平上不同于正态分布,说明数据可能存在非对称性。而峰度系数均在1%的水平上区别于正态分布,一致表明其厚尾特征。状态转移过程正好能捕捉上述数据特征,可作为消费增长过程的一个合理设定。

(二)消费增长状态转移模型的构造

模型的初始设定为：

值得指出的是,在进行以k状态模型为原假设,以k+1状态模型为备择假设的检验时,由于原假设下某些参数不能识别以及似然函数的得分向量为零,似然比统计量不再具有标准的卡方分布。本文应用瑟凯蒂等(Cecchetti等,1990)和兰姆(Lam,1990)的Monte Carlo方法解决这一问题。首先在原假设下估计模型得到参数估计值;接着在原假设下,以参数估计值作为真实参数值生成数据,并利用生成的数据分别在原假设和备择假设下对模型进行估计;最后计算准似然比统计量的值①该值为备择假设和原假设下的对数似然函数值之差的两倍。。将上述过程模拟1 000次,这1 000个准似然比统计量形成的经验分布用于检验。

具体计算中,以单状态模型为原假设、最一般的两状态模型为备择假设的似然比统计量,用全国人均增长率和全国城镇人均增长率计算的值分别为195和211,在1%的显著性水平上就能拒绝原假设;而以两状态模型为原假设、最一般的三状态模型为备择假设的似然比统计量分别为9.76和10.30,这在通常的5%显著性水平上都无法拒绝原假设。因此确定最优的状态个数为2。

(三)消费增长过程模型的确定

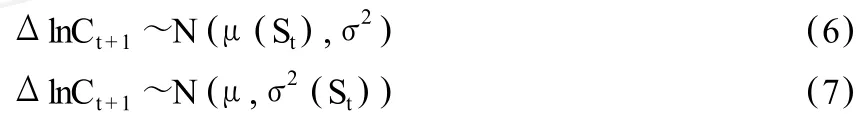
模型(6)和模型(7)分别是消费增长均值和方差之中的一个参数随状态变化,而另一参数不随状态变化。进而分别以模型(6)和模型(7)为原假设、备择假设均为模型(4),通过检验来判断消费增长能否由更精简(parsimonious)的模型来刻画。

表2报告了模型(4)、(6)、(7)的估计结果。从其中的LR统计量可以判断,第一组检验中,模型(6)被拒;而第二组检验中,模型(7)不能被拒绝。因此模型(7)可作为消费增长过程的一种精简设定。而模型(7)仅考虑到消费增长的方差随状态变化,为进一步考虑消费增长均值随状态变化对市场收益率的影响,模型(4)可作为消费增长过程更一般的设定来作比较研究。

四、均衡资产定价

我们在Lucas模型和消费增长的特定过程的基础上求解均衡状态下的资产收益率。首先列出求解该问题的相关条件和假设：

1.由Lucas模型中经济人优化问题的一阶必要条件,即(3)式反复迭代,可得当期的资产价格为当期消费和未来预期消费的非线性函数：

表2 状态转移模型的极大似然估计

2.将服从2状态Markov转移过程的消费增长过程即(4)式表达为：

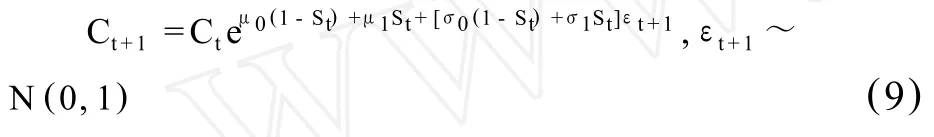
根据上述假设,本文采用待定系数法来求解该资产定价问题。设定解的形式为：

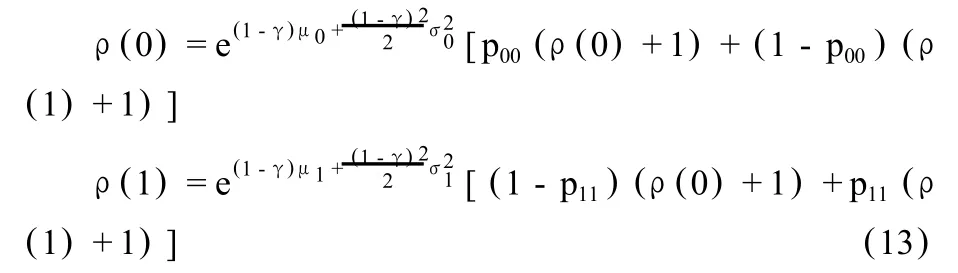
其解①只要ρ(0)＞0和ρ(1)＞0,则期望方程(3)式的横截面条件成立,从而(8)式收敛。为：

该定价方程有许多有趣的性质。首先,资产价格与消费成正比;在该模型中,价格消费比只取2个值,ρ(0)或ρ(1),这是因为假设经济人在时期t能观测到状态变量St。在更为现实的情况下,St不可观测,但可以估计出来,这时价格消费比的取值在ρ(0)和ρ(1)之间,为一可连续取值的变量。其次,价格消费比取决于相对风险规避系数和经济所处的状态St。

由于状态变量St同时影响消费增长的均值和方差,在此首先分析仅均值随状态变量St变化时对价格消费比的影响,即先约束来分析价格消费比的影响因素。对两状态的模型的估计中有μ1＞μ0(4),即状态0为低增长状态而状态1为高增长状态。当时,低增长状态时的价格消费比ρ(0)大于(等于、小于)高增长状态时的价格消费比ρ(0)当且仅当相对风险规避系数大于(等于、小于)1。这是因为若当期经济处于高增长状态时,下一期很有可能还是高增长状态,经济人预测到未来具有更高的禀赋期望表明未来产品具有更低的相对价格,从而会促使经济人增加储蓄和增加对资产的需求,导致当期的资产价格提高,这是跨期相对价格效应(收入效应)。同时更高的禀赋期望也会导致经济人为了平滑消费而增加当期的消费,进而卖掉他的部分资产,导致当期资产价格的下降,这属于跨期消费平滑效应(替代效应)。这两种效应的作用方向正好相反,而它们力量的强弱与相对风险规避系数的大小①在消费效用函数为常相对风险规避系数的模型中,相对风险规避系数与消费的跨期替代弹性互为相反数,经济人对风险的厌恶程度与其平滑消费的意愿无法区分。当经济人进行跨期消费投资决策时,经济人对风险的厌恶在此被解释为具有平滑消费的意愿似乎更为合理。密切相关。当γ=1时(对数消费效用函数),跨期相对价格效应与跨期消费平滑效应正好相抵,即(8)式中Ct,价格消费比为一常数。当γ＜1时,跨期相对价格效应起主导作用,从而高增长状态时有较高的价格消费比。当γ＞1时,跨期消费平滑效应起主导作用,从而高增长状态时有较低的价格消费比。

进而分析方差随状态变量St变化时对价格消费比的影响。当可以看出,无论相对风险规避系数γ如何取值,高波动状态下的价格消费比ρ(0)都大于低波动状态下的价格消费比ρ(1)。这是因为若当期经济处于高波动状态,下一期很有可能还是高波动状态,由于经济人对风险的厌恶,因此会增加储蓄而购买资产,从而导致资产价格升高。

从(9)式和(10)式有：均衡状态的总收益率为

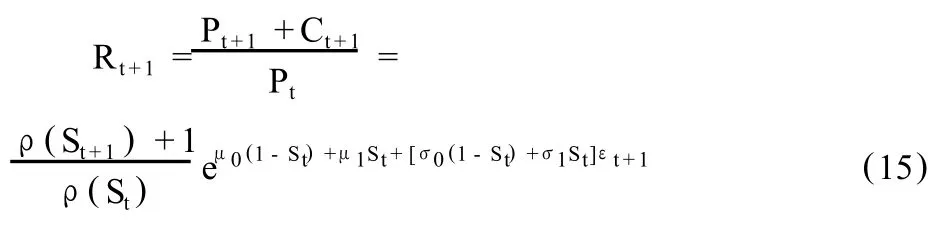
五、收益率的均值回复检验

利用上述理性预期模型的收益率的显式表达式,我们将研究两个问题：第一,理性预期模型的收益率是否真正存在均值回复特征;第二,上证指数的实际收益率的均值回复现象能否由该理性预期模型所解释。我们用方差率统计量来检验理性预期模型的收益率是否存在均值回复现象。方差率的定义如下：设Rt为单期的资产实际收益率,为第t期到第t+k-1期收益率的综合,即则时间阶数为k的方差率为VR(k)=Var它也可表达为单期收益率自相关系数的加权平均其中ρj为单期收益率的j阶相关系数。如果收益率是序列无相关的,则方差率在大样本的情况下,对于所有的k来说都等于1,这常被作为“市场有效”的原假设,因为这时股票价格服从随机游走。如果股票价格呈现均值回复现象(收益率的自相关系数为负),则方差率小于1。

对于第一个问题,我们首先模拟理性预期模型下的收益率序列,然后计算模拟收益率序列的方差率。具体模拟步骤如下：1)给定p和q,生成序列生成序列σ2,利用(15)式得到收益序列并且计算该样本的方差率统计量。将上述步骤重复10 000次,可得到方差率的经验分布,取其中位数来判断模型收益率是否存在均值回复特征。模拟过程中的模型参数(p,q,μ,σ1,σ2)来源于消费增长过程的极大似然估计值(见表2),时间贴现β设为0.99。本节选取模型(4)和模型(7)作为模拟对象,模型(7)只反映宏观消费状态波动的变化,而模型(4)还体现了宏观消费状态在高涨与低迷之间的变化。

Poterba和Summers(1988)对一些常用的衡量均值回复特征的统计量进行模拟实验的结果表明方差率是最具有势(Power)的统计量。尽管如此,方差率在小样本下仍然存在较大的偏差,此时单期收益率自相关系数的估计是有偏的;因而当收益率各期相互独立时,方差率统计量的均值也可能小于1。模拟中我们将模拟样本数设定为1960以避免方差率统计量存在的小样本偏差问题。

对于第二个问题,本文参照瑟凯蒂(Cecchetti等,1990)、博诺莫和加西亚(Bonomo和Garcia, 1994)的方法,将模拟收益率序列的方差率统计量的中位数作为其均值回复程度的估计,并给出该统计量的合理置信区间,来判断上证指数收益率的均值回复现象是否能由该理性预期模型所解释。具体做法是：在理性预期模型的模拟收益率序列中选取共196个样本点来计算与实际样本相对应的方差率。实际样本的股票收益率研究区间从1993年7月到2009年10月①这是由于在1993年7月之前我国股市还处于不规范的初期发展阶段,当时股市中的股票数量少,上市规模也不大,股市经常处于大起大落的状态,这些不规范数据对于分析整个股市的特征会造成扭曲。,为196个月;因为1990年1月为可获得的消费月度数据的初始时间,因此模拟收益率序列中选取1990年1月到2009年10月的数值,238个样本点。同样将模拟过程重复10 000次来得到统计量的模拟分布,并由此判断上证指数的方差率统计量是否在其模拟分布合理的范围内。

均衡资产定价模型表明,风险规避系数γ对反映消费增长的均值随状态变量St变化时,对消费价格比的影响有重要作用,所以需在不同γ的设定下模拟收益率以分析其均值回复特征。表3列出了对于参数γ的不同设定、消费增长过程为模型(4)和模型(7)时,方差率统计量模拟分布的中位数②本文仅列出消费增长过程的参数设定为全国人均消费数据估计的结果,由于全国城镇人均消费数据得到的参数估计结果与之近似,其得到的方差率统计量的结果也类似,故不再列出。。从表中可以看出,无论是哪种消费增长过程的设定,当相对风险规避系数γ较小时,模型产生的收益率序列都不具有明显的均值回复特征,但随着γ的增大,收益率序列的均值回复特征就越来越明显。具体而言,模型(4)的收益率序列具有更明显的均值回复特征,γ=4的收益率序列已有很明显的均值回复现象;对于模型(7),参数γ=5的收益率序列也具有明显的均值回复特征。

从模型(7)来看,宏观消费状态总会从低波动状态进入到一个高波动状态,然后再进入一个低波动状态,同时资产的价格消费比也经历着一个从低到高,进而又降低的过程,如同经济周期的繁荣、衰退,周而复始,这时资产价格的均值回复现象就产生了。如果宏观消费状态的变化还包括增长率大小的变化,如模型(4),那么资产的价格消费比的变化就更加明显,均值回复特征也就更加明显。这源于经济人存在着规避风险和平滑消费的意愿,随着风险规避系数γ的增大(平滑消费的意愿增强),这种均值回复特征也越明显。

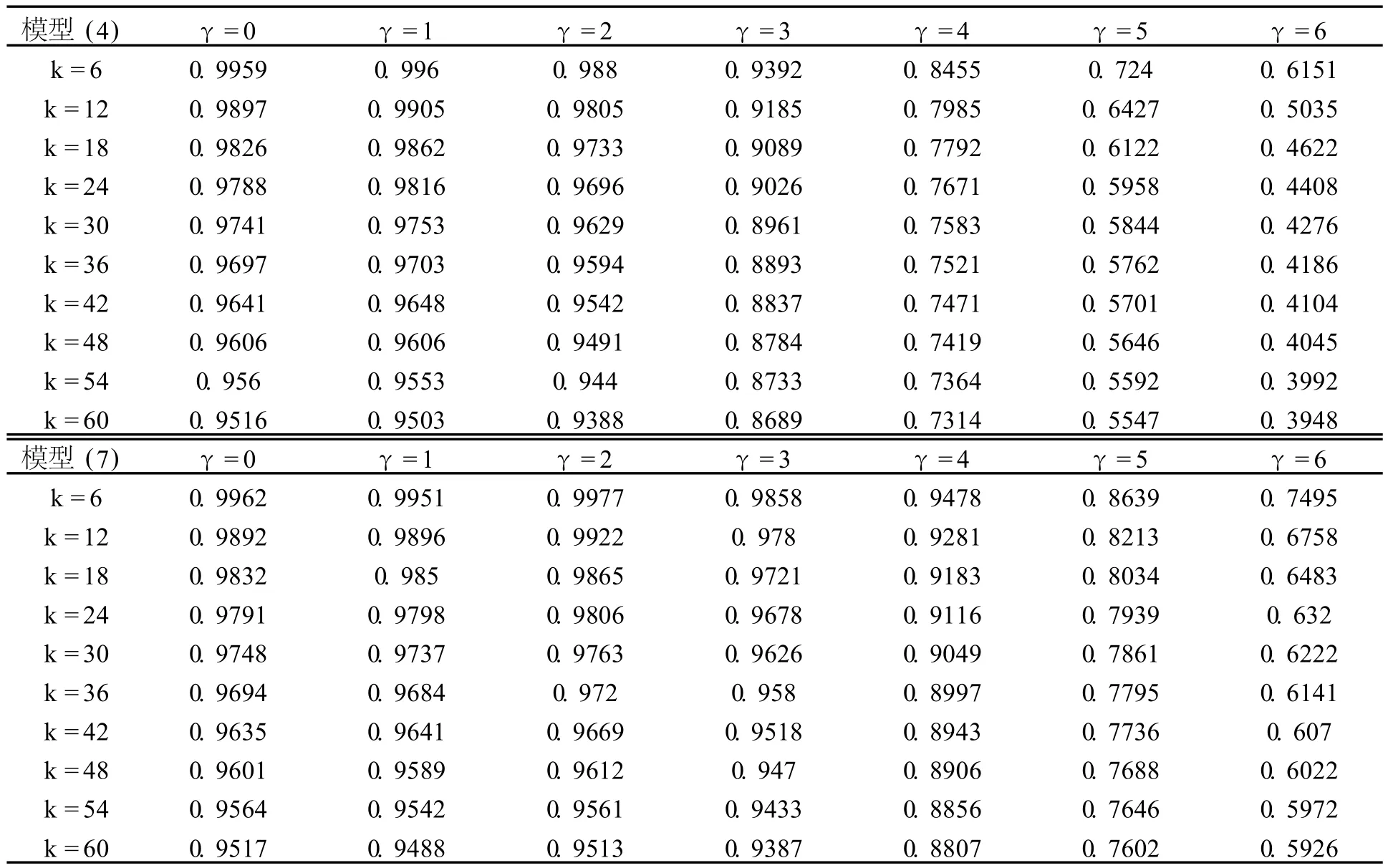
表3 均衡模型收益率的方差率(模拟样本量为1960)

我们进而考察上证指数的实际收益率的均值回复现象能否由该理性预期模型所解释,分别考虑模型(4)取γ=4和模型(7)取γ=5时模拟收益率序列,此时收益率序列具有均值回复特征;另外还考虑这两个模型在γ=2时的模拟收益率序列,此时不具有均值回复特征。分别对这两类模拟收益率序列按实际样本数计算方差率的模拟分布,以判断实际观察到的均值回复现象是缘于经济人厌恶风险和平滑消费的理性行为还是缘于小样本的偏差。表4和表5分别列出了模型(4)和模型(7)在不同γ取值时的模拟收益率序列按实际样本数计算的方差率中位数,以及上证指数算术平均和加权平均下对应的P-值,并且图示于图1和图2。

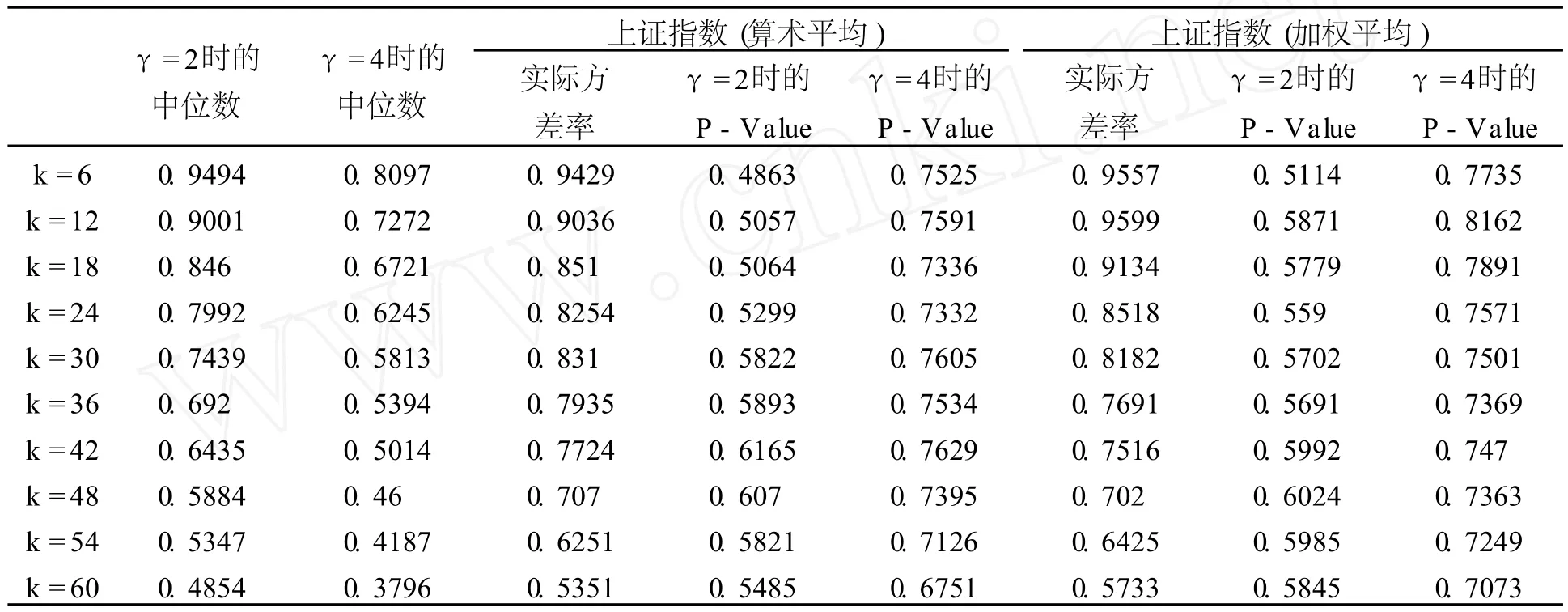
表4 模型(4)下均衡收益的方差率与实际方差率(样本量为196)

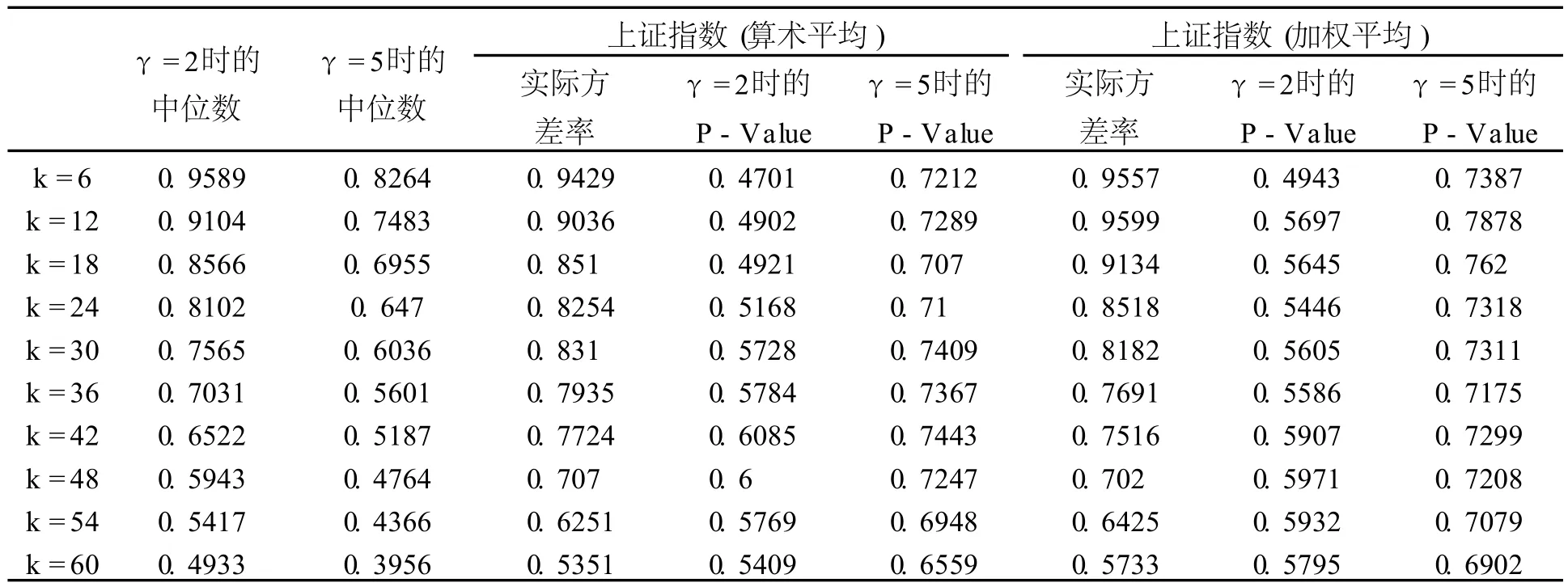
表5 模型(7)下均衡收益的方差率与实际方差率(样本量为196)

比较表4、表5按实际样本数计算的方差率中位数与表3中不同相对风险规避系数设定下对应的大样本的方差率中位数,可以看出,模拟样本量为1960时方差率的中位数与实际样本量为196时的方差率中位数差别较为明显。可见在实际样本数下对均值回复进行检验都存在小样本偏差问题,即使选取频率高的数据,该小样本偏差问题也很难解决①比如计算收益率5年的自相关系数需要5年以上的时间,而不是利用周数据或日数据能解决的。。

从表4和表5的P-Value(方差率的模拟值小于实际方差率的比例,即实际方差率在模拟分布中的位置)可以看出,均值回复特征不明显的均衡模型(γ=2时)和具有均值回复特征的均衡模型(γ=4和γ=5时)都能产生实际中观察到的均值回复现象。具体而言,对于γ=2的模型,实际方差率在其方差率模拟分布的40%分位数和60%分位数之间,而γ=4或γ=5时的模型,实际方差率在其方差率模拟分布的60%分位数和80%分位数之间。对于通常90%的置信区间(5%分位数到95%分位数)而言,这些模型都无法被拒绝。也就是说,实际观察到的均值回复现象既可以是小样本偏差的结果(γ=2时的情况),也可以是具有风险厌恶的经济人的理性预期的结果(γ=4或5时的情况),即经济人对风险的厌恶以及对消费进行平滑的结果,从而使得收益率出现均值回复特征。

图1 模型(4)下均衡收益的方差率与实际方差率(样本量为196)

图2 模型(7)下均衡收益的方差率与实际方差率(样本量为196)

六、结 论

本文将Lucas(1978)模型与Hamilton(1989)的状态转移模型结合起来,推导出一个理性定价模型;通过计算该模型均衡状态下模拟收益率的方差率统计量在实际样本数下的Monte Carlo分布,得出在该样本数下,上证指数的实际方差率统计量与Monte Carlo分布的中位数相差无异,两者均表现出均值回复现象。换言之,上证指数出现的均值回复现象可与该均衡资产定价模型的均值回复现象相一致。模拟分析过程还表明,产生这种均值回复特征的原因,可能是实际检验过程的小样本偏差,也可能是理性经济人对风险的厌恶和平滑消费的结果。因此,均值回复现象不能作

为拒绝我国股票市场有效性的证据。

Balvers,R,YWu,and E Gilliland,Mean reversion across national stock markets and parametric contrarian investment strategies,The Journal of Finance,2000,(55)：745—772.

Bansal,R,and A Yaron,Risks for the long run：A potential resolution of asset pricing puzzles,The Journal of Finance, 2004,(59)：1481—1509.

Bonomo,M,and R Garcia,Can a well-fitted equilibrium asset-pricing model produce mean reversion?,Journal of Applied Econometrics,1994,(9)：19—29.

Cecchetti,S G,P SLam,and N CMark,Mean reversion in equilibrium asset prices,The American Economic Review, 1990,(80)：398—418.

Chaudhuri,K,and Y Wu,Random walk versus breaking trend in stock prices：Evidence from emergingmarkets,Journal ofBanking and Finance,2003,(27)：575—92.

Fama,E F,and K R French,Per manent and temporary components of stock prices,The Journal of Political Economy, 1988,(96)：246.

Findley,D F,B C Monsell,W R Bell,M C Otto,and BC Chen,New capabilities and methods of the x-12-arima seasonal-adjustment program,Journal of Business&Economic Statistics,1998：127—152.

Gangopadhyay,P,and MR Reinganum,Interpreting mean reversion in stock returns,Quarterly Review of Economics and Finance,1996,(36)：377—394.

Gropp,J,Mean reversion of industry stock returns in the us, 1926—1998,Journal of Empirical Finance,2004,(11)：537—551.

Hamilton,J D,A new approach to the economic analysis of nonstationary ti me series and the business cycle,Econometrica, 1989,(57)：357—384.

Jegadeesh,N,Seasonality in stock price mean reversion：Evidence from the us and the uk,The Journal of Finance, 1991,(46)：1427—1444.

Kandel,S,and R F Stambaugh,Expectations and volatility of consumption and asset returns,Review of Financial Studies, 1990：207—232.

Kandel,S,R F Stambaugh,Asset returns and intertemporal preferences,Journal of Monetary Economics,1991,(27)：39—71.

Kim,M J,C R Nelson,and R Startz,Mean reversion in stock prices?A reappraisal of the empirical evidence,The Review of Economic Studies,1991,(58)：515—528.

Ki m,C J,and C R Nelson,Has the us economy become more stable?A bayesian approach based on a markov-switching model of the business cycle,Review of Economics and Statistics,1999,(81)：608—616.

Lam,P,The hamilton model with a general autoregressive component：Estimation and comparison with other models of economic ti me series,Journal ofMonetary Economics,1990, (26)：409—432.

Lettau,M,S C Ludvigson,and J A Wachter,The declining equity premium：What role does macroeconomic risk play?, Review of Financial Studies,2008,(21)：1653—1687.

Lo,AW,and AC MacKinlay,The size and power of the variance ratio test in finite samples：A monte carlo investigation,Journal of Econometrics,1989,(40)：203—238.

Lucas,R E,Asset prices in an exchange economy,Econometrica,1978,(46)：1429—1445.

Malliaropulos,D,and R Priestley,Mean reversion in southeast asian stock markets,Journal of Empirical Finance, 1999,(6)：355—384.

McConnell,MM,and G Perez-Quiros,Output fluctuations in the united states：What has changed since the early 1980's?, American Economic Review,2000：1464—1476.

McQueen,G,Long-horizon mean-revertingstockprices revisited,Journal of Financial and Quantitative Analysis, 1992：1—18.

Nam,K,C S Pyun,andA C Arize,Asymmetricmean-reversion and contrarian profits：Anst-garch approach,Journal of Empirical Finance,2002,(9)：563—588.

Poterba,J M,and L H Summers,Mean reversion in stock prices：Evidence and implications,Journal of Financial Economics,1988,(22)：27—59.

Rapach,D E,JK Strauss,and G Zhou,Out-of-sample equity premium prediction：Combination forecasts and links to the real economy,Review of Financial Studies,2010,(23)：821

Richardson,M,Temporary components of stock prices：A skeptic's view,Journal of Business&Economic Statistics, 1993：199—207.

Richardson,M,and JH Stock,Drawing inferences from statistics based on multiyear asset returns,Journal of Financial Economics,1989,(25)：323—348.

宋玉臣,寇俊生.沪深股市均值回归的实证检验.金融研究,2005,(12).

赵振全,苏治,丁志国.我国股票市场收益率非对称均值回归特征的计量检验——基于ANST-GARCH模型的实证分析.数量经济技术经济研究,2005,(22).

【责任编辑：许玉兰;责任校对：许玉兰,杨海文】

F830.91

A

1000-9639(2010)06-0182-10

2010—07—29

王美今(1949—),女,福建泉州人,中山大学岭南学院教授、博士生导师(广州510275);

陈 锐(1983—),男,湖南湘潭人,中山大学岭南学院博士研究生(广州510275)。